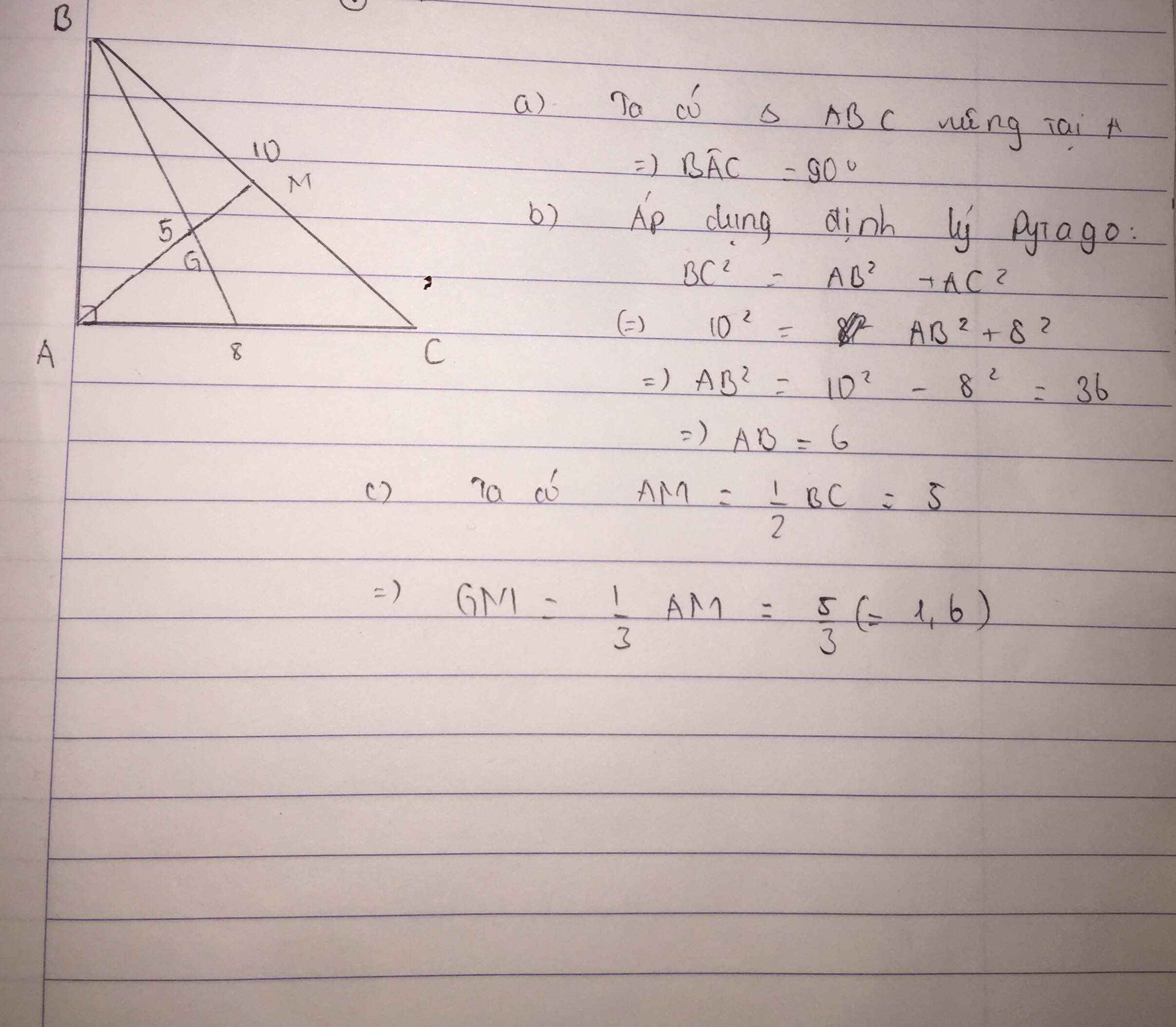Cậu tham khảo:

Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác.

Độ dài trung tuyến AM là:

A. 8cm

B.

54

cm

C.

44

cm

Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Vẽ trung tuyến AM của tam giác.Độ dài trung tuyến AM là:

A. 8cm

B.54cm

C.44cm

D. 6cm

Câu 1: A

Câu 2: A

1.A

2.A

c

C

Xét \(\Delta ABC\) vuông tại \(A\) có:

\(BC^2=AB^2+AC^2\) (định lí pitago)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét \(\Delta ABC\) vuông tại \(A\)  có: 

\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) (định lí đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)

\(\Rightarrow\) Chọn đáp án \(C\)

a: Xét ΔABC có 

AM là trung tuyến

AM=BC/2

=>ΔABC vuông tại A

b: AB=căn 10^2-8^2=6cm

c: GM=1/3*AM=5/3(cm)

a: Xét ΔABM và ΔACM có

AB=AC
AM chung

BM=CM

Do đó: ΔABM=ΔACM

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: BM=CM=BC/2=8(cm)

nên AM=6(cm)

tham khảo

a: Xét ΔABM và ΔACM có

AB=AC
AM chung

BM=CM

Do đó: ΔABM=ΔACM

b: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường cao

c: BM=CM=BC/2=8(cm)

nên AM=6(cm)

a, Ta có :

AB = AC (gt)

=> Δ ABC cân tại A

Xét Δ ABM và Δ ACM, có :

AB = AC (gt)

MB = MC (M là trung điểm BC)

\(\widehat{ABM}=\widehat{ACM}\) (Δ ABC cân tại A)

=> Δ ABM = Δ ACM

b, Ta có :

AM là đường trung tuyến

Δ ABC cân tại A

=> AM ⊥ BC

c, Ta có :

BC = 2MB

=> 16 = 2MB

=> MB = 8 (cm)

Xét Δ AMB vuông tại M, có :

\(AB^2=AM^2+BM^2\)

=> \(10^2=AM^2+8^2\)

=> \(AM^2=36\)

=> AM = 6 (cm)

BC=12cm

Dễ và cơ bản mà nhỉ:vv

a) Xét ∆ABM và ∆ACM:

AB=AC (∆ABC cân tại A)

BM=CM (AM là trung tuyến)

\(\widehat{ABM}=\widehat{ACM}\) (∆ABC cân tại A)

=> ∆ABM=∆ACM (c.g.c)

b) Theo câu a: ∆ABM=∆ACM 

=> \(\widehat{AMB}=\widehat{AMC}\)

Mà \(\widehat{AMB}+\widehat{AMC}=180^o\) (2 góc kề bù)

=> \(\widehat{AMB}=\widehat{AMC}=90^o\)

=> AM vuông góc với BC

c) M là trung điểm của BC

=> \(MB=MC=\dfrac{BC}{2}=\dfrac{6}{2}=3\)

Áp dụng định lý Py-ta-go vào ∆ABM, ta có:

\(AB^2=AM^2+BM^2\)

\(\Leftrightarrow5^2=AM^2+3^2\Rightarrow AM^2=5^2-3^2=16=4^2\)

\(\Rightarrow AM=4\) (cm)

Vậy AM=4cm.

b) Cm theo cách khác:

Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: MB=MC(M là trung điểm của BC)

nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)

Từ (1) và (2) suy ra AM là đường trung trực của BC

hay AM\(\perp\)BC(đpcm)

a) Xét ΔABM và ΔACM có

AB=AC(ΔABC cân tại A)

AM chung

BM=CM(M là trung điểm của BC)

Do đó: ΔABM=ΔACM(c-c-c)