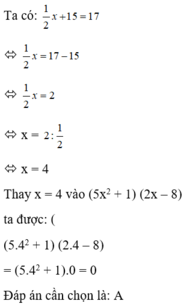|x2 + 1| = |12x - 5|

Những câu hỏi liên quan
a) x + 7 ⋮ x + 2
b) 2x + 5 ⋮ x + 1
c) 3x - 2 ⋮ x + 3
d) 12x + 1 ⋮ 3x + 2
e) x2 + 3x + 5 ⋮ x + 3
f) X2 - 2x + 3 ⋮ x + 2
a: \(x+7⋮x+2\)
=>\(x+2+5⋮x+2\)
=>\(5⋮x+2\)
=>\(x+2\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{-1;-3;3;-7\right\}\)
b: \(2x+5⋮x+1\)
=>\(2x+2+3⋮x+1\)
=>\(3⋮x+1\)
=>\(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
c: \(3x-2⋮x+3\)
=>\(3x+9-11⋮x+3\)
=>\(-11⋮x+3\)
=>\(x+3\in\left\{1;-1;11;-11\right\}\)
=>\(x\in\left\{-2;-4;8;-14\right\}\)
d: \(12x+1⋮3x+2\)
=>\(12x+8-7⋮3x+2\)
=>\(-7⋮3x+2\)
=>\(3x+2\in\left\{1;-1;7;-7\right\}\)
=>\(3x\in\left\{-1;-3;5;-9\right\}\)
=>\(x\in\left\{-\dfrac{1}{3};-1;\dfrac{5}{3};-3\right\}\)
e: \(x^2+3x+5⋮x+3\)
=>\(x\left(x+3\right)+5⋮x+3\)
=>\(5⋮x+3\)
=>\(x+3\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{-2;-4;2;-8\right\}\)
f: \(x^2-2x+3⋮x+2\)
=>\(x^2+2x-4x-8+11⋮x+2\)
=>\(11⋮x+2\)
=>\(x+2\in\left\{1;-1;11;-11\right\}\)
=>\(x\in\left\{-1;-3;9;-13\right\}\)
Đúng 1
Bình luận (0)
Tính giá trị của (5 x 2 + 1)(2x – 8) biết 1 2 x + 15 = 17
A. 0
B. 10
C. 47
D. -3
Các cặp phương trình sau đây có tương đương không? Vì sao?a)
x
2
−
6
x
+
9
0
và
x
2
+
1
2
x
−
6
0
b)
x
2...
Đọc tiếp
Các cặp phương trình sau đây có tương đương không? Vì sao?
a) x 2 − 6 x + 9 = 0 và x 2 + 1 2 x − 6 = 0
b) x 2 + 1 2 x − 1 = 0 và 2 x 4 + 1 = 0
(X2+12X+36)(5-3X)≤0
\(\Leftrightarrow\left(x+6\right)^2\left(5-3x\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-6\\x\ge\dfrac{5}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Thực hiện phép chia:
1. (-3x3 + 5x2 - 9x + 15) : ( 3x + 5)
2. ( 5x4 + 9x3 - 2x2 - 4x - 8) : ( x-1)
3. ( 5x3 + 14x2 + 12x + 8 ) : (x + 2)
4. ( x4 - 2x3 + 2x -1 ) : ( x2 - 1)
5. ( 5x2 - 3x3 + 15 - 9x ) : ( 5 - 3x)
6. ( -x2 + 6x3 - 26x + 21) : ( 3 -2x )
1: Sửa đề: 3x-5
\(=\dfrac{-x^2\left(3x-5\right)-3\left(3x-5\right)}{3x-5}=-x^2-3\)
2: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
=5x^2+14x^2+12x+8
3: \(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}=5x^2+4x+4\)
4: \(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}=x^2+1-2x\)
5: \(=\dfrac{x^2\left(5-3x\right)+3\left(5-3x\right)}{5-3x}=x^2+3\)
Đúng 3
Bình luận (0)
1) (x2-4x+16) (x+4)-x(x+1) (x+2)+3x2=0
2) (8x+2) (1-3x)+(6x-1) (4x-10)=-50
3) (x2+2x+4) (2-x)+x(x-3) (x+4)-x2+24=0
4) (\(\dfrac{x}{2}\)x2+3) (5-6x)+(12x-2) (\(\dfrac{x}{4}\)x4+3)=0
1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
Đúng 1
Bình luận (0)
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)
Đúng 1
Bình luận (0)
3)(x2+2x+4)(2-x)+x(x-3)(x+4)-x2+24=0
\(\Rightarrow\)8-x3+x(x2+4x-3x-12)-x2+24=0
\(\Rightarrow\)8-x3+x3+4x2-3x2-12x-x2+21=0
\(\Rightarrow\)-12x+29=0
\(\Rightarrow\)-12x=-29
\(\Rightarrow\)x=\(\dfrac{-29}{-12}=\dfrac{29}{12}\)
Đúng 1
Bình luận (0)
1/ Thực hiện phép nhân :
a) x2 ( 5x3 - x - \(\dfrac{1}{2}\))
b) ( 3xy - x2 + y ) \(\dfrac{2}{3}\)x2y
c) x2 ( 4x3 - 5xy + 2x ) ( -\(\dfrac{1}{2}\) xy )
2/ Tìm x, biết
a) 3x( 12x - 4 ) - 9x (4x - 3 ) = 30
b ) x( 5 - 2x ) + 2x ( x - 1 )= 15
2.
a. 3x(12x - 4) - 9x(4x - 3) = 30
<=> 36x2 - 12x - 36x2 + 27x = 30
<=> 36x2 - 36x2 - 12x + 27x = 30
<=> 15x = 30
<=> x = 2
b. x(5 - 2x) + 2x(x - 1) = 15
<=> 5x - 2x2 + 2x2 - 2x = 15
<=> -2x2 + 2x2 + 5x - 2x = 15
<=> 3x = 15
<=> x = 5
Đúng 1
Bình luận (0)
a) x2 ( 5x3 - x - 2323x2y= 6969x3y2- 2323x4y+ 2323x2y2
c) x2 ( 4x3 - 5xy + 2x ) ( -
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau:
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2);
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2).
ai làm đúng thì kết bạn với mình nha!
a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
Đúng 0
Bình luận (0)
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
= 0 - 0
= 0
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2)
= (x-xx+1) : (2x-2) : (x-xx+1) : (2x-2)
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
= -2x-1-xx2+1. (14 - 4x)
= -x2-1-xx2+14-4x
= -6x-xx2+13
Đúng 0
Bình luận (0)
a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
Đúng 0
Bình luận (0)
Giải các phương trình sau:a, (9x2 - 4)(x + 1) (3x +2)(x2 - 1)b, (x - 1)2 - 1 + x2 (1 - x)(x + 3)c, (x2 - 1)(x + 2)(x - 3) (x - 1)(x2 - 4)(x + 5)d, x4 + x3 + x + 1 0e, x3 - 7x + 6 0f, x4 - 4x3 + 12x - 9 0g, x5- 5x3 + 4x 0h, x4 - 4x3 + 3x2 + 4x - 4 0
Đọc tiếp
Giải các phương trình sau:
a, (9x2 - 4)(x + 1) = (3x +2)(x2 - 1)
b, (x - 1)2 - 1 + x2 = (1 - x)(x + 3)
c, (x2 - 1)(x + 2)(x - 3) = (x - 1)(x2 - 4)(x + 5)
d, x4 + x3 + x + 1 = 0
e, x3 - 7x + 6 = 0
f, x4 - 4x3 + 12x - 9 = 0
g, x5- 5x3 + 4x = 0
h, x4 - 4x3 + 3x2 + 4x - 4 = 0
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
Đúng 0
Bình luận (0)
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
Đúng 0
Bình luận (0)
Giải phương trình bằng phương pháp đưa về dạng ước số:
a) x2-x=y2-1
b) x2+12x=y2
c) x2+xy-2y-x-5=0
Lời giải:
a.
$x^2-x=y^2-1$
$\Leftrightarrow x^2-x+1=y^2$
$\Leftrightarrow 4x^2-4x+4=4y^2$
$\Leftrightarrow (2x-1)^2+3=(2y)^2$
$\Leftrightarrow 3=(2y)^2-(2x-1)^2=(2y-2x+1)(2y+2x-1)$
Đến đây xét các TH:
TH1: $2y-2x+1=1; 2y+2x-1=3$
TH2: $2y-2x+1=-1; 2y+2x-1=-3$
TH3: $2y-2x+1=3; 2y+2x-1=1$
TH4: $2y-2x+1=-3; 2y+2x-1=-1$
b.
$x^2+12x=y^2$
$\Leftrightarrow (x+6)^2=y^2+36$
$\Leftrightarrow 36=(x+6)^2-y^2=(x+6-y)(x+6+y)$
Đến đây xét trường hợp tương tự phần a.
c.
$x^2+xy-2y-x-5=0$
$\Leftrightarrow x^2+xy=x+2y+5$
$\Leftrightarrow 4x^2+4xy=4x+8y+20$
$\Leftrightarrow (2x+y)^2=4x+8y+20+y^2$
$\Leftrightarrow (2x+y)^2-2(2x+y)+1=y^2+6y+21$
$\Leftrightarrow (2x+y-1)^2=(y+3)^2+12$
$\Leftrightarrow (2x+y-1)^2-(y+3)^2=12$
$\Leftrightarrow (2x+y-1-y-3)(2x+y-1+y+3)=12$
$\Leftrightarrow (2x-4)(2x+2y+2)=12$
$\Leftrightarrow (x-2)(x+y+1)=3$
Đến đây đơn giản rồi.
Đúng 2
Bình luận (0)
a) \(x^2-x=y^2-1\)
\(\Rightarrow x^2-x+1=y^2\)
\(\Rightarrow4x^2-4x+4=4y^2\)
\(\Rightarrow4x^2-4x+1+3=\left(2y\right)^2\)
\(\Rightarrow\left(2x+1\right)^2-\left(2y\right)^2=-3\)
\(\Rightarrow\left(2x-2y+1\right)\left(2x+2y+1\right)=-3\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}\left(2x-2y+1\right)\left(2x+2y+1\right)\in Z\\\left(2x-2y+1\right)\left(2x+2y+1\right)\inƯ\left(7\right)\end{matrix}\right.\)
Ta có bảng:
| x-y | -1 | 0 | -2 | 1 |
| x+y | 1 | -2 | 0 | -1 |
| x | 0 | -1 | -1 | 0 |
| y | 1 | -1 | -1 | -1 |
Vậy \(\left(x,y\right)\in\left\{\left(0;1\right);\left(-1;-1\right);\left(-1;-1\right);\left(0;-1\right)\right\}\)
Đúng 0
Bình luận (0)