Giải phương trình lượng giác sau
\(2cos^3x+2sin^3x+2sin^2xcosx+2cos^2xsinx-\sqrt{2}=0\)
Giải phương trình :
2sin^2xcosx + sin3x =4cos^3x
(sin2x)^3-(cos2x)^3+2cos^2x=1
Em ms hok cái này nên ko chắc lắm ạ :))
a/ \(\Leftrightarrow2\sin^2x.\cos x+3\sin x-4\sin^3x-4\cos^3x=0\)
Xét \(\sin^3x=0\) ko phải là nghiệm của PT
Xét \(\sin^3x\ne0\)
\(\Leftrightarrow2.\cot x+\frac{3}{\sin^2x}-4-4.\cot^3x=0\)
\(\Leftrightarrow4\cot^3x-3\cot^2x-2\cot x+1=0\)
Sau đó chị giải nghiệm là xong, thú thật e kém về phần gpt b3 trở lên nên sợ sai lắm :))
câu b khá là dài vì phải phân tích cos^3 2x nên ngày mai e giải nốt ạ :))
Giải phương trình sau:
a) 3sin^3x + 2sin^2x.cosx = sinx.cos^2x
b) 6sinx + 2cos^3x = 5sin2x.cosx
a/
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(3tan^3x+2tan^2x=tanx\)
\(\Leftrightarrow tanx\left(3tan^2x+2tanx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=0\\3tan^2x+2tanx-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=0\\tanx=-1\\tanx=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=-\frac{\pi}{4}+k\pi\\x=arctan\left(\frac{1}{3}\right)+k\pi\end{matrix}\right.\)
b/ \(\Leftrightarrow3sinx+cos^3x=5sinx.cos^2x\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(3tanx.\frac{1}{cos^2x}+1=5tanx\)
\(\Leftrightarrow3tanx\left(1+tan^2x\right)-5tanx+1=0\)
\(\Leftrightarrow3tan^3x-2tanx+1=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(3tan^2x-3tanx+1\right)=0\)
\(\Leftrightarrow tanx=-1\Rightarrow x=-\frac{\pi}{4}+k\pi\)
giải phương trình:
1) \(2\sqrt{2}cos^3x\left(x-\frac{\pi}{4}\right)-3cosx-sinx=0\)
2) \(tanx.sin^2x-2sin^2x=3\left(cos2x+sinxcosx\right)\)
3) \(2sin^3x=cosx\)
4) \(6sinx-2cos^3x=\frac{5sin4xcosx}{2cos2x}\)
giải phương trình lượng giác
\(2cos^2x-1=sin3x\)
\(2sin^4x-5sin^3x-sin^2x+3sinx+1=0\)
\(sin^6x+cos^6x=2cos^2\left(\frac{\pi}{4}-x\right)\)
a/
\(\Leftrightarrow cos2x=sin3x\)
\(\Leftrightarrow cos2x=cos\left(\frac{\pi}{2}-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-3x+k2\pi\\2x=3x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{10}+\frac{k2\pi}{5}\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx+1\right)\left(sin^2x-2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\frac{1}{2}\\sinx=1-\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow x=...\)
c/
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=1+cos\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow1-3sin^2x.cos^2x=1+sin2x\)
\(\Leftrightarrow-\frac{3}{4}sin^22x=sin2x\)
\(\Leftrightarrow3sin^22x+4sin2x=0\)
\(\Leftrightarrow sin2x\left(3sin2x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sin2x=-\frac{4}{3}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=\frac{k\pi}{2}\)
Giải phương trình lượng giác:
1. 2Sin^3x - sin^2xcosx - 2SinxCos^2x=Cos^3x
2. 4Sin^3x + 3Cos^3x=3Sinx(1+(Sin2x)/2)
giai pt
a) \(2sin^3x=cosx\)
b) \(sin^3x+cos^3x=sinx-cosx\)
c) \(4cos^3x+2sin^3x-3sinx=0\)
d) \(2cos^3x+2sinx-3sinx.sin2x=0\)
a/ Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow2tan^3x=\frac{1}{cos^2x}\)
\(\Leftrightarrow2tan^3x=1+tan^2x\)
\(\Leftrightarrow2tan^3x-tan^2x-1=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(2tan^2x+tanx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\2tan^2x+tanx+1=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=\frac{\pi}{4}+k\pi\)
b/
\(\Leftrightarrow sin^3x-sinx+cos^3x+cosx=0\)
\(\Leftrightarrow-sinx\left(1-sin^2x\right)+cos^3x+cosx=0\)
\(\Leftrightarrow-sinx.cos^2x+cos^3x+cosx=0\)
\(\Leftrightarrow cosx\left(cos^2x-sinx.cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\\cos^2x-sinx.cosx+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\frac{1}{2}+\frac{1}{2}cos2x-\frac{1}{2}sin2x+1=0\)
\(\Leftrightarrow cos2x-sin2x=-3\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=\frac{3}{\sqrt{2}}>1\left(vn\right)\)
c/
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(4+2tan^3x-3tanx.\frac{1}{cos^2x}=0\)
\(\Leftrightarrow2tan^3x-3tanx\left(1+tan^2x\right)+4=0\)
\(\Leftrightarrow-tan^3x-3tanx+4=0\)
\(\Leftrightarrow\left(1-tanx\right)\left(tan^2x+tanx+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tan^2x+tanx+4=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=\frac{\pi}{4}+k\pi\)
d/
\(\Leftrightarrow2cos^3x+2sinx-6sin^2x.cosx=0\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(2+2tanx.\frac{1}{cos^2x}-6tan^2x=0\)
\(\Leftrightarrow1+tanx\left(1+tan^2x\right)-3tan^2x=0\)
\(\Leftrightarrow tan^3x-3tan^2x+tanx+1=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(tan^2x-2tanx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tan^2x-2tanx-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=1-\sqrt{2}\\tanx=1+\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{3\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\end{matrix}\right.\)
Giải phương trình: 2sin2x + 2cos4x = 2cos2x + sinx.cosx
ta có : \(2sin^2x+2cos^4x=2cos^2x+sinx.cosx\)
\(\Leftrightarrow2sin^2x+2cos^2x\left(cos^2x-1\right)-sinx.cosx=0\)
\(\Leftrightarrow2sin^2x-2cos^2x.sin^2x-sinx.cosx=0\)
\(\Leftrightarrow2sin^2x\left(1-cos^2x\right)-sinx.cosx=0\)
\(\Leftrightarrow2sin^4x-sinx.cosx=sinx\left(2sin^3x-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\2sin^3x-cosx=0\end{matrix}\right.\)
tới đây bn giải như phương trình dạng bình thường nha :)
Giải pt:
a, \(sin2x+2cos^2x=2\)
b, \(2sin^2x+sinx.cosx-cos^2x=0\)
a: =>sin2x+2*(1-cos2x)/2=2
=>sin2x-cos2x=1
=>căn 2*sin(2x-pi/4)=1
=>2x-pi/4=pi/4+k2pi hoặc 2x-pi/4=3/4pi+k2pi
=>x=pi/4+kpi hoặc x=pi/2+kpi
b: =>2*(1+cos2x)/2+1/2*sin2x-1/2(1-cos2x)=0
=>1+cos2x+1/2*sin2x-1/2+1/2cos2x=0
=>1/2*sin2x+3/2*cos2x=-1/2
=>sin(2x+a)=-cos(a)=cos(pi-a)
=>sin(2x+a)=sin(-pi/2+a)
=>2x+a=-pi/2+a+k2pi hoặc 2x+a=3/2pi-a+k2pi
=>x=-pi/4+kpi hoặc x=3/4pi-a+kpi
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 2 sin 2 x - 2 cos 2 x = 2 bằng:
A. 0
B. π 4
C. - 3 π 4
D. - π 4
Chọn D.
Phương pháp: Giải phương trình và tìm nghiệm âm lớn nhất, nghiệm dương nhỏ nhất.
Cách giải: Ta có:
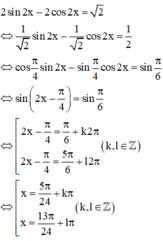
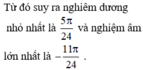
Vậy tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
2
sin
2
x
-
2
cos
2
x
=
2
![]()
Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình bằng 2sin 2x-2cos 2x = 2
A. 0
B. π 4
C. - 3 π 4
D. - π 4