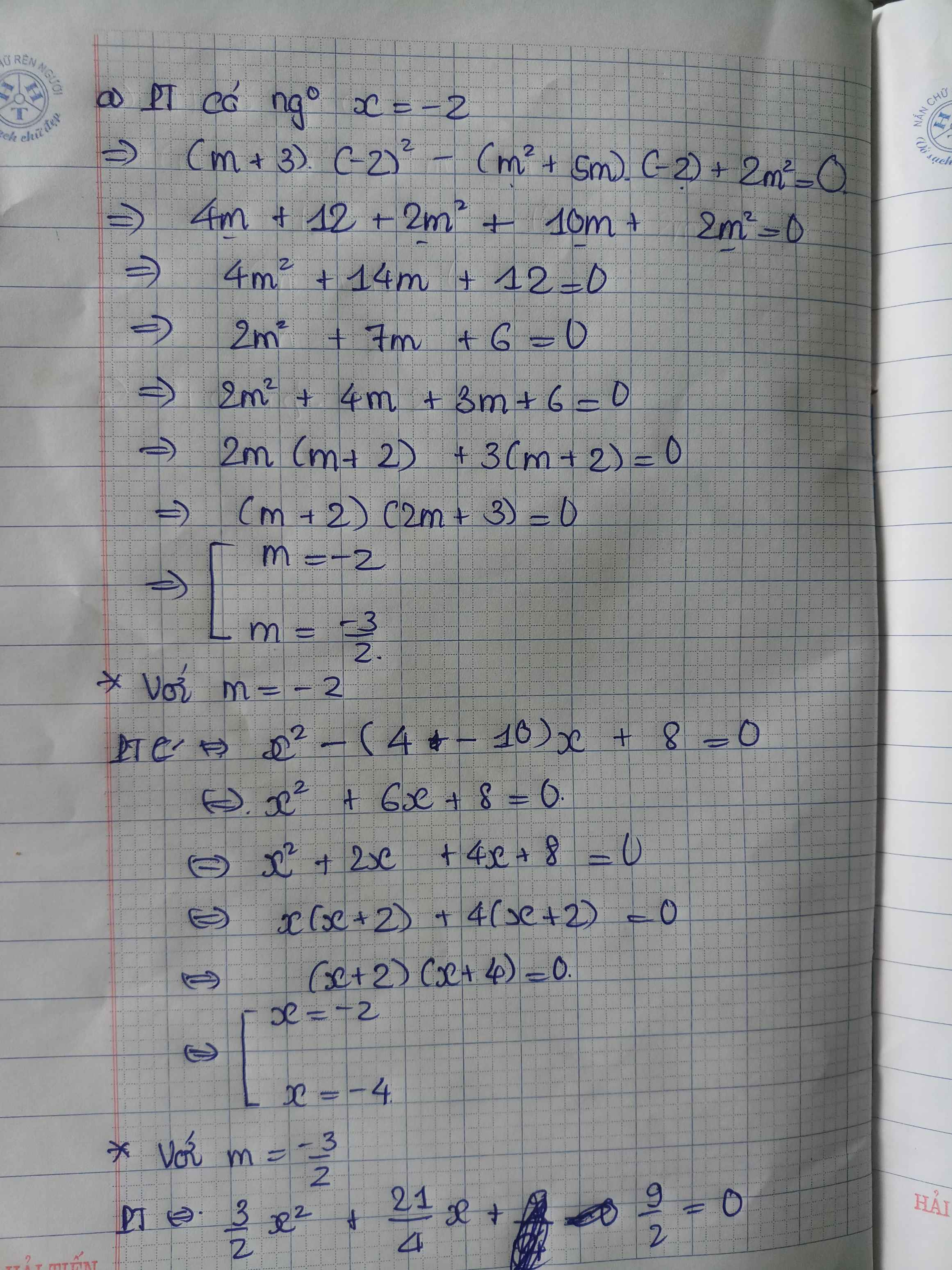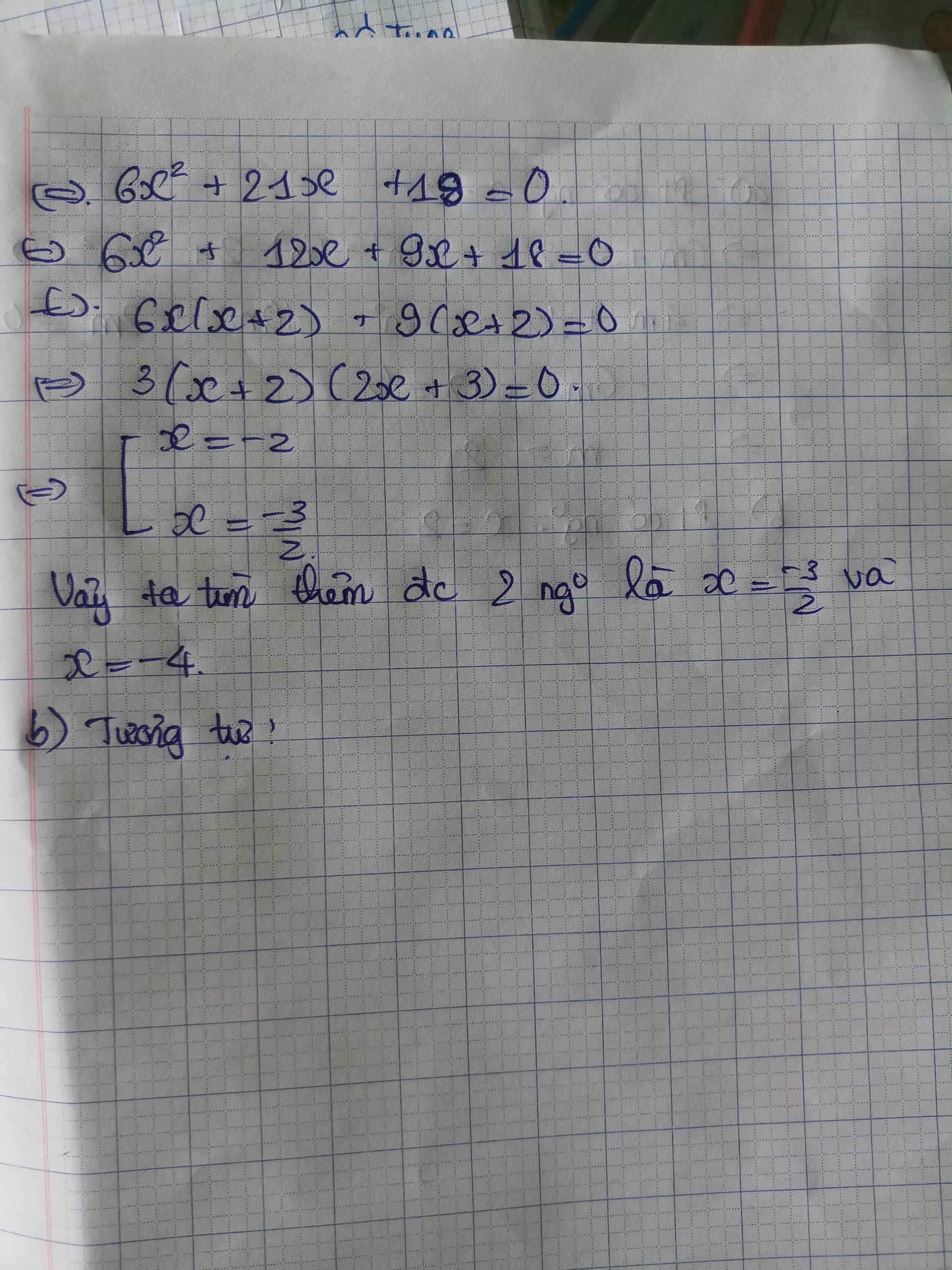Xét pt (1): \(6x-5m=3+3mx\Leftrightarrow\left(3m-6\right)x=-5m-3\)

Để pt có nghiệm \(\Rightarrow m\ne2\) khi đó \(x=\dfrac{-5m-3}{3m-6}\)

Xét pt (2): \(\left(x+1\right)\left(x-1\right)-\left(x+2\right)^2=3\)

\(\Leftrightarrow x^2-1-x^2-4x-4=3\Rightarrow4x=-8\Rightarrow x=-2\)

Để nghiệm của (1) gấp 2 lần nghiệm của (2)

\(\Rightarrow\dfrac{-5m-3}{3m-6}=-2.2=-4\)

\(\Leftrightarrow-5m-3=-12m+24\Rightarrow m=\dfrac{27}{7}\)

(2) (x+1)(x-1) - (x+2)² = 3

<=> x² - 1 - x² - 4x - 4 - 3 = 0

<=> -4x - 8 = 0

<=> -4(x - 2) = 0

<=> x - 2 = 0

<=> x = 2

Ta có x₁ = 2 . x₂

=> x₁ = 2.2 = 4

(1) 6x - 5m = 3 + 3mx

<=> 24 - 5m = 3 + 12m

<=> 24 - 3 = 12m + 5m

<=> 21 = 17m

<=> m = \(\dfrac{17}{21}\)

\(Pt\left(1\right)\): \(3mx-1=5m-x\) \(\Leftrightarrow\) \(3mx+x=5m+1\) \(\Leftrightarrow\) \(\left(3m+1\right)x=5m+1\) \(\Leftrightarrow\) \(x=\frac{5m+1}{3m+1}\)
\(Pt\left(2\right)\) : \(m-x=3mx+1\) \(\Leftrightarrow m-1=3mx+x\) \(\Leftrightarrow\) \(\left(3m+1\right)x=m-1\)\(\Leftrightarrow\) \(x=\frac{m-1}{3m+1}\)
Để \(pt\left(1\right)\) và \(pt\left(2\right)\) có cùng nghiệm thì \(\frac{5m+1}{3m-1}=\frac{m-1}{3m+1}\)\(\Leftrightarrow\)\(5m+1=m-1\)\(\Leftrightarrow\)\(4m=-2\Leftrightarrow m=-\frac{1}{2}\)

a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)

\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)

=>4m=-13

hay m=-13/4

c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)

\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)

=>-8m>=-4

hay m<=1/2

a: Δ=(-2m)^2-4*3*1=4m^2-12

Để phương trình có nghiệm kép thì 4m^2-12=0

=>m^2=3

=>\(m=\pm\sqrt{3}\)

b: 

TH1: m=0

=>-6x-3=0

=>x=-1/2(nhận)

TH2: m<>0

Δ=(-6)^2-4*4m*(-m-3)

=36-16m(-m-3)

=36+16m^2+48m

=16m^2+48m+36

Để phương trình có nghiệm kép thì 16m^2+48m+36=0

=>m=-3/2

c: TH1: m=-2

=>-2(-2-1)x+4=0

=>6x+4=0

=>x=-2/3(nhận)

TH2: m<>-2

Δ=(2m-2)^2-4(m+2)*4

=4m^2-16m+4-16m-32

=4m^2-32m-28

Để pt có nghiệm kép thì 4m^2-32m-28=0

=>\(m=\dfrac{16\pm6\sqrt{11}}{5}\)

d: TH1: m=6

=>18x-2=0

=>x=1/9(nhận)

TH2: m<>6

Δ=(3m)^2-4*(-2)(m-6)

=9m^2+8m-48

Để pt có nghiệm kép thì 9m^2+8m-48=0

=>\(m=\dfrac{-4\pm8\sqrt{7}}{9}\)

\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)

a. \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1=3x_2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x_2=2\left(m+1\right)\\x_1=3x_2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{2}\\x_1=\dfrac{3\left(m+1\right)}{2}\end{matrix}\right.\)

Lại có \(x_1x_2=2m+10\Rightarrow\left(\dfrac{m+1}{2}\right)\left(\dfrac{3\left(m+1\right)}{2}\right)=2m+10\)

\(\Leftrightarrow3m^2+6m+3=8m+40\)

\(\Leftrightarrow3m^2-2m-37=0\Rightarrow m=\dfrac{1\pm4\sqrt{7}}{3}\)

b.

\(P=-\left(x_1+x_2\right)^2-8x_1x_2\)

\(=-4\left(m+1\right)^2-8\left(2m+10\right)\)

\(=-4m^2-24m-84=-4\left(m+3\right)^2-48\le-48\)

\(P_{max}=-48\) khi \(m=-3\)

a) Ta có: \(\Delta=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(2m+10\right)\)

\(=\left(2m+2\right)^2-4\left(2m+10\right)\)

\(=4m^2+8m+4-8m-40\)

\(=4m^2-36\)

Để phương trình có nghiệm thì \(4m^2-36\ge0\)

\(\Leftrightarrow4m^2\ge36\)

\(\Leftrightarrow m^2\ge9\)

\(\Leftrightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)

Khi \(m\ge3\) hoặc \(m\le-3\) thì Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1\cdot x_2=2m+10\\x_1+x_2=2\left(m+1\right)=2m+2\end{matrix}\right.\)

mà \(x_1-3x_2=0\) nên ta lập được hệ phương trình:

\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_2=2m+2\\x_1=3x_2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=3\cdot x_2\\x_2=\dfrac{m+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{3m+3}{2}\\x_2=\dfrac{m+1}{2}\end{matrix}\right.\)

Thay \(x_1=\dfrac{3m+3}{2};x_2=\dfrac{m+1}{2}\) vào \(x_1\cdot x_2=2m+10\), ta được:

\(\dfrac{3m+3}{2}\cdot\dfrac{m+1}{2}=2m+10\)

\(\Leftrightarrow\dfrac{3\left(m+1\right)^2}{4}=2m+10\)

\(\Leftrightarrow3\left(m^2+2m+1\right)=8m+40\)

\(\Leftrightarrow3m^2+6m+3-8m-40=0\)

\(\Leftrightarrow3m^2-2m-37=0\)

\(\Delta=\left(-2\right)^2-4\cdot3\cdot\left(-37\right)=4+444=448>0\)

Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}m_1=\dfrac{2+8\sqrt{7}}{6}=\dfrac{4\sqrt{7}+1}{3}\left(nhận\right)\\m_2=\dfrac{2-8\sqrt{7}}{6}=\dfrac{1-4\sqrt{7}}{3}\left(nhận\right)\end{matrix}\right.\)

b) Thay x=2 vào pt, ta được:

\(4\left(m^2-1\right)-4m+m^2+m+4=0\)

\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)

\(\Leftrightarrow5m^2-3m=0\)

\(\Leftrightarrow m\left(5m-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)

Áp dụng hệ thức Vi-et, ta được:

\(x_1+x_2=\dfrac{2m}{m^2-1}\)

\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)

kh biết