Cho tam giác ABC vuông tại A đường cao AH đường tròn (A;AH) kẻ các tiếp tuyến BD, CE với đường tròn (A). Chứng minh BD.CE ≤ BC^2/ AH
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH vẽ đường tròn tâm B bán kính ba, lấy điểm D thuộc đường tròn nằm trong tam giác ABC, tia CD cắt đường cao AH tại F và cắt đường tròn (B) tại E, qua điểm D vẽ đường thằng song song với AE cắt ah tại N và AC. Chứng minh:
1. Góc ABD = 2 lần góc MDC
2. CD.CD = CA^2
2: Xét ΔCAD và ΔCEA có
góc C chung
góc CAD=góc CEA
=>ΔCAD đồng dạng với ΔCEA
=>CA/CE=CD/CA
=>CA^2=CE*CD
Bài 1:Cho tam giác cân ABC,AB=AC=6cm,đường cao AH=5cm.Gọi O là đường tròn tam giác ABC
a)Vì sao điểm O nằm trên AH
b)Tính độ dài đường kính AD của đường tròn tâm O
Bài 2:Cho tam giác ABC vuông tại A,đường cao AH,biết AH=12cm,HB=18cm.Tính bán kính đường tròn tam giác ABC
cho tam giác ABC vuông tại A đường cao AH . Biết AH=12cm ,HB=8cm .Tính bán kính đường tròn ngoại tiếp tam giác ABC
Vì ΔABC vuông tại A nên ΔABC nội tiếp đường tròn đường kính BC
hay R=BC/2
\(AH^2=HB\cdot HC\)
=>HC=144:8=18(cm)
=>BC=26(cm)
=>R=13(cm)
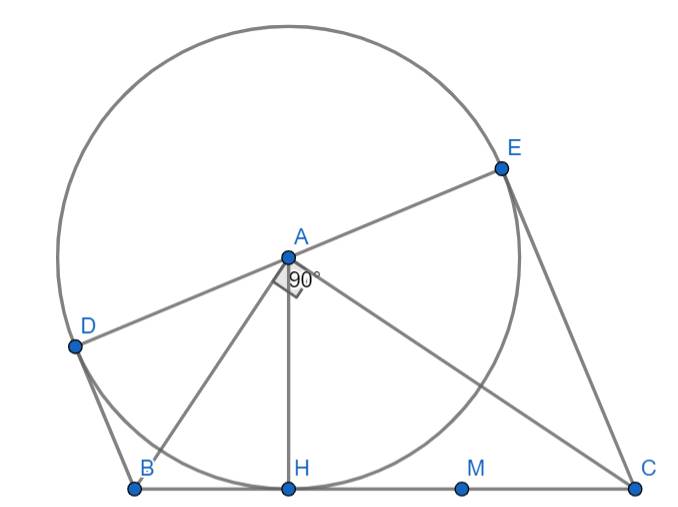
Cho tam giác ABC vuông tại A, vẽ đường cao AH của tam giác ABC.Vẽ đường tròn tâm (A) bán kính AH , vẽ E đối xứng H qua A. Vễ tiếp tuyến với đường tròn tại E cắt CA tại D. Chứng minh: BD tiếp xúc với đường tròn tâm A bán kính AH.
.png)
Xét tam giác vuông AHC và tam giác vuông AED có:
AE = AH
\(\widehat{HAC}=\widehat{EAD}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AHC=\Delta AED\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow AC=AD\)
Xét tam giác BDC có BA là đường cao đồng thời trung tuyến nên nó là tam giác cân. Vậy thì BA cũng là tia phân giác góc B.
Gọi H' là chân đường vuông góc hạ từ A xuống BD.
Ta thấy ngay \(\Delta H'BA=\Delta HBA\) (Cạnh huyền góc nhọn)
Vậy thì AH' = AH
Suy ra BD là tiếp tuyến của đường tròn tâm A, bán kính AH.
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm A bán kính AH và kẻ thêm đường kính HD của đường tròn đó. Từ D kẻ tiếp tuyến với đường tròn, cắt AC kéo dài tại E.
a.Chứng minh rằng tam giác BEC là tam giác cân tại B.
b.Chứng minh rằng BE là tiếp tuyến của đường tròn tâm A bán kính AH.
Cho tam giác ABC vuông tại A, đường cao AH, biết HB=2cm, HC=18cm. TÍnh độ dài AB;AH và diện tích đường tròn ngoại tiếp tam giác ABC
AH=căn 2*18=6cm
AB=căn 6^2+2^2=2*căn 10(cm)
bài 1: tam giác ABC vuông tại A đường cao AB/AC =3/4; BC= 10. tính AH, BH
bài 2: cho tam giác ABC vuông tại A đường cao AH=33,6 biết AB/AC =27/4 tính các cạnh của tam giác ABC
bài 3: cho tam giác ABC vuông tại A đường cao AH tính đường cao AH,AB,AC nếu biết BH=36; CH=64
1
\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{.4}AC\)
Theo pytago xét tam giác ABC vuông tại A có:
\(\sqrt{AB^2+AC^2}=BC^2\\ \Rightarrow\sqrt{\left(\dfrac{3}{4}AC\right)^2+AC^2}=10\\ \Rightarrow AC=8\\ \Rightarrow AB=\dfrac{3.8}{4}=6\)
Theo hệ thức lượng xét tam giác ABC vuông tại A, đường cao AH có:
\(AB^2=BH.BC\\ \Leftrightarrow BH=\dfrac{AH^2}{BC}=\dfrac{6^2}{10}=3,6\)
2
\(\dfrac{AB}{AC}=\dfrac{27}{4}\Rightarrow AB=\dfrac{27}{4}AC\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{27}{4}AC\right)^2+AC^2}=\dfrac{\sqrt{745}AC}{4}\) ( Theo pytago trong tam giác ABC vuông tại A)
Theo hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH có:
\(AH.BC=AB.AC\\ \Leftrightarrow33,6.\dfrac{\sqrt{745}}{4}AC=\dfrac{27}{4}AC.AC\\ \Rightarrow AC=\dfrac{56\sqrt{745}}{45}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{27}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{42\sqrt{745}}{5}\\BC=\dfrac{\sqrt{745}}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{2086}{9}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}AC\approx33,97\\AB\approx229,28\\BC\approx231,78\end{matrix}\right.\)
3
`BC=HB+HC=36+64=100`
Theo hệ thức lượng có (trong tam giác ABC vuông tại A đường cao AH):
\(AH^2=HB.HC\\ \Rightarrow AH=\sqrt{36.64}=48\)
\(AB=\sqrt{HB.BC}=\sqrt{36.100}=60\\ AC=\sqrt{HC.BC}=\sqrt{64.100}=80\)
Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm A, bán kính AH cắt đường tròn đường kính BC tại hai điểm M và N. MN cắt AH tại I. Chứng minh rằng I là trung điểm của AH
Cho tam giác ABC vuông tại A, đường cao AH. Dựng đường tròn tâm O đường kính AB. Cho biết số đo góc ABC = 60 độ và AB = a . Tính theo a diện tích phần tam giác. ABC nằm ngoài đường tròn (O)