Tìm m để phương trình: \(1+sin^2x=\left(m+1\right)\left(1+cos^{2020}x\right)\) có nghiệm

Những câu hỏi liên quan
1. Giải các phương trình sau:
a) \(\cos\left(x+15^0\right)=\dfrac{2}{5}\)
b) \(\cot\left(2x-10^0\right)=4\)
c) \(\cos\left(x+12^0\right)+\sin\left(78^0-x\right)=1\)
2. Định m để các phương trình sau có nghiệm:
\(\sin\left(3x-27^0\right)=2m^2+m\)
c.
\(\Leftrightarrow cos\left(x+12^0\right)+cos\left(90^0-78^0+x\right)=1\)
\(\Leftrightarrow2cos\left(x+12^0\right)=1\)
\(\Leftrightarrow cos\left(x+12^0\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+12^0=60^0+k360^0\\x+12^0=-60^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=48^0+k360^0\\x=-72^0+k360^0\end{matrix}\right.\)
2.
Do \(-1\le sin\left(3x-27^0\right)\le1\) nên pt có nghiệm khi:
\(\left\{{}\begin{matrix}2m^2+m\ge-1\\2m^2+m\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m+1\ge0\left(luôn-đúng\right)\\2m^2+m-1\le0\end{matrix}\right.\)
\(\Rightarrow-1\le m\le\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
a.
\(\Rightarrow\left[{}\begin{matrix}x+15^0=arccos\left(\dfrac{2}{5}\right)+k360^0\\x+15^0=-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-15^0+arccos\left(\dfrac{2}{5}\right)+k360^0\\x=-15^0-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
b.
\(2x-10^0=arccot\left(4\right)+k180^0\)
\(\Rightarrow x=5^0+\dfrac{1}{2}arccot\left(4\right)+k90^0\)
Đúng 1
Bình luận (0)
2.
Phương trình \(sin\left(3x-27^o\right)=2m^2+m\) có nghiệm khi:
\(2m^2+m\in\left[-1;1\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m\le1\\2m^2+m\ge-1\end{matrix}\right.\)
\(\Leftrightarrow\left(m+1\right)\left(2m-1\right)\le0\)
\(\Leftrightarrow-1\le m\le\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
cho hàm số \(f\left(x\right)=\dfrac{9^x}{9^x+3}\). Tìm m để phương trình \(f\left(3m+\dfrac{1}{4}\sin x\right)+f\left(\cos^2x\right)=1\) có đúng 8 nghiệm phân biệt thuộc [0;3pi]
\(f\left(1-x\right)+f\left(x\right)=\dfrac{9^{1-x}}{9^{1-x}+3}+\dfrac{9^x}{9^x+3}=\dfrac{9}{9+3.9^x}+\dfrac{9^x}{9^x+3}=\dfrac{3}{9^x+3}+\dfrac{9^x}{9^x+3}=1\)
\(\Rightarrow f\left(x\right)=1-f\left(1-x\right)\)
\(\Rightarrow f\left(cos^2x\right)=1-f\left(sin^2x\right)\)
Do đó:
\(f\left(3m+\dfrac{1}{4}sinx\right)+f\left(cos^2x\right)=1\)
\(\Leftrightarrow f\left(3m+\dfrac{1}{4}sinx\right)=f\left(sin^2x\right)\) (1)
Hàm \(f\left(x\right)=\dfrac{9^x}{9^x+3}\) có \(f'\left(x\right)=\dfrac{3.9^x.ln9}{\left(9^x+3\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow\left(1\right)\Leftrightarrow3m+\dfrac{1}{4}sinx=sin^2x\)
Đến đây chắc dễ rồi, biện luận để pt \(sin^2x-\dfrac{1}{4}sinx=3m\) có 8 nghiệm trên khoảng đã cho
Đúng 2
Bình luận (0)
tìm m để phương trình \(m\cos x+\left(m-1\right)\sin x=3-2m\) có nghiệm
uốn giải bài này nhanh bạn cần biết đến công thức
PT:a.sinx +b.cosx =c có nghiệm khi:a2+b2≥c2a2+b2≥c2
ADCT:(m−1)2+m2≥3−2m(m−1)2+m2≥3−2m
⇔m2≥1⇔m2≥1
[m≥1m≤−1
Đúng 0
Bình luận (0)
1. Tìm m để PT có nghiệm:
a) \(\sqrt{3}\cos^2x+\dfrac{1}{2}\sin2x=m\)
b) \(3\sin^2x-2\sin x\cos x+m=0\)
c) \(\sin^2x+2\left(m-1\right)\sin x\cos x-\left(m+1\right)\cos^2x=m\)
b.
\(\Leftrightarrow\dfrac{3}{2}\left(1-cos2x\right)-sin2x+m=0\)
\(\Leftrightarrow sin2x+\dfrac{3}{2}cos2x-\dfrac{3}{2}=m\)
\(\Leftrightarrow\dfrac{\sqrt{13}}{2}\left(\dfrac{2}{\sqrt{13}}sin2x+\dfrac{3}{\sqrt{13}}cos2x\right)-\dfrac{3}{2}=m\)
Đặt \(\dfrac{2}{\sqrt{13}}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\dfrac{\sqrt{13}}{2}sin\left(2x+a\right)-\dfrac{3}{2}=m\)
Phương trình có nghiệm khi và chỉ khi:
\(\dfrac{-\sqrt{13}-3}{2}\le m\le\dfrac{\sqrt{13}-3}{2}\)
Đúng 2
Bình luận (0)
Lý thuyết đồ thị:
Phương trình \(f\left(x\right)=m\) có nghiệm khi và chỉ khi \(f\left(x\right)_{min}\le m\le f\left(x\right)_{max}\)
Hoặc sử dụng điều kiện có nghiệm của pt lương giác bậc nhất (tùy bạn)
a.
\(\dfrac{\sqrt{3}}{2}\left(1-cos2x\right)+\dfrac{1}{2}sin2x=m\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x+\dfrac{\sqrt{3}}{2}=m\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)+\dfrac{\sqrt{3}}{2}=m\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi:
\(-1+\dfrac{\sqrt{3}}{2}\le m\le1+\dfrac{\sqrt{3}}{2}\)
Đúng 3
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos2x+\left(m-1\right)sin2x-\left(m+1\right)\left(\dfrac{1}{2}+\dfrac{1}{2}cos2x\right)=m\)
\(\Leftrightarrow\left(2m-2\right)sin2x-\left(m+2\right)cos2x=3m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt có nghiệm khi:
\(\left(2m-2\right)^2+\left(m+2\right)^2\ge9m^2\)
\(\Leftrightarrow m^2+m-2\le0\)
\(\Leftrightarrow-2\le m\le\)
Đúng 2
Bình luận (0)
1. Tìm m để PT có nghiệm:
a) \(\sqrt{3}\cos^2x+\dfrac{1}{2}\sin2x=m\)
b) \(3\sin^2x-2\sin x\cos x+m=0\)
c) \(^{ }\sin^2x+2\left(m-1\right)\sin x\cos x-\left(m+1\right)\cos^2x=m\)
a) \(\sqrt{3}\left(\dfrac{1+cos2x}{2}\right)+\dfrac{1}{2}sin2x=m\) ↔ \(\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x=m-\dfrac{\sqrt{3}}{2}\)
→\(\sqrt{3}cos2x+sin2x=2m-\sqrt{3}\) ↔ \(2cos\left(\dfrac{\pi}{6}-2x\right)=2m-\sqrt{3}\)
→\(cos\left(\dfrac{\pi}{6}-2x\right)=m-\dfrac{\sqrt{3}}{2}\)
Pt có nghiệm khi và chỉ khi \(-1\le m-\dfrac{\sqrt{3}}{2}\le1\)
b) \(\left(3+m\right)sin^2x-2sinx.cosx+mcos^2x=0\)
cosx=0→ sinx=0=> vô lý
→ sinx#0 chia cả 2 vế của pt cho cos2x ta đc:
\(\left(3+m\right)tan^2x-2tanx+m=0\)
pt có nghiệm ⇔ △' ≥0
Tự giải phần sau
c) \(\left(1-m\right)sin^2x+2\left(m-1\right)sinx.cosx-\left(2m+1\right)cos^2x=0\)
⇔cosx=0→sinx=0→ vô lý
⇒ cosx#0 chia cả 2 vế pt cho cos2x
\(\left(1-m\right)tan^2x+2\left(m-1\right)tanx-\left(2m+1\right)=0\)
pt có nghiệm khi và chỉ khi △' ≥ 0
Tự giải
Đúng 1
Bình luận (0)
c. Tìm m để phương trình
\(msin^2x-\left(m-1\right)sin2x+\left(2m+1\right)cos^2x=0\) vô nghiệm.
C) Pt \(\Rightarrow m\cdot\dfrac{1-cos2x}{2}-\left(m-1\right)sin2x+\left(2m+1\right)\cdot\dfrac{1+cos2x}{2}=0\)
\(\Rightarrow\left(m+1\right)cos2x-\left(2m-2\right)sin2x=-1-3m\)
Pt có nghiệm: \(\Leftrightarrow\) \(\left(m+1\right)^2+\left[-\left(2m-2\right)\right]^2\ge\left(1+3m\right)^2\)
\(\Rightarrow\dfrac{-3-\sqrt{13}}{2}\le m\le\dfrac{-3+\sqrt{13}}{2}\)
Pt vô nghiệm: \(\Rightarrow\left\{{}\begin{matrix}m>\dfrac{-3+\sqrt{13}}{2}\\m< \dfrac{-3-\sqrt{13}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình sau:
a, \(\sin\left(2x\right)+\sin\left(x\right)-\dfrac{1}{2\sin\left(x\right)}-\dfrac{1}{\sin\left(2x\right)}=2\cot\left(2x\right)\)
b, \(\left(\sin\left(2x\right)+cos\left(2x\right)\right)cos\left(x\right)+2cos\left(2x\right)-sin\left(x\right)=0\)
c, \(\sin\left(2x\right)-\cos\left(2x\right)+3\sin\left(x\right)-\cos\left(x\right)-1=0\)
b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x = 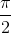 + kπ ⇔ x =
+ kπ ⇔ x = 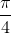 + k
+ k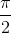 (k ∈
(k ∈ 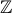 )
)
Đúng 0
Bình luận (0)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)
Đúng 0
Bình luận (0)
cho phương trình \(2cos2x+sin^2xcosx+sinxcos^2x=m\left(sinx+cosx\right)\)tìm m để phương trình có ít nhất 1 nghiệm thuộc đoạn\(\left[0;\dfrac{\Pi}{2}\right]\)
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)
Đúng 0
Bình luận (0)
Tìm nghiệm dương nhỏ nhất của phương trình
\(\cos\pi\left(x^2+2x-\dfrac{1}{2}\right)=\sin\left(\pi x^2\right)\)
\(\Leftrightarrow cos\left(\pi x^2+2\pi x-\dfrac{\pi}{2}\right)=sin\left(\pi x^2\right)\)
\(\Leftrightarrow sin\left(\pi x^2+2\pi x\right)=sin\left(\pi x^2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\pi x^2+2\pi x=\pi x^2+k2\pi\\\pi x^2+2\pi x=\pi-\pi x^2+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\left(1\right)\\2x^2+2x-2k-1=0\left(2\right)\end{matrix}\right.\)
(1) có nghiệm dương nhỏ nhất \(x=1\)
Xét (2), để (2) có nghiệm \(\Rightarrow\Delta'=1+2\left(2k+1\right)\ge0\) \(\Rightarrow k\ge0\)
Khi đó (2) có 2 nghiệm: \(\left[{}\begin{matrix}x=\dfrac{-1-\sqrt{4k+3}}{2}< 0\\x=\dfrac{-1+\sqrt{4k+3}}{2}\ge\dfrac{\sqrt{3}-1}{2}\end{matrix}\right.\)
\(\Rightarrow\) Nghiệm dương nhỏ nhất của pt đã cho là \(x=\dfrac{\sqrt{3}-1}{2}\)
Đúng 0
Bình luận (0)
1) Giải phương trình: \(\left(2021x-2020\right)^3=8\left(x-1\right)^3+\left(2019x-2018\right)^3\)
2) Cho phương trình ẩn x: \(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\) , với m là tham số. Tìm tất cả các giá trị của tham số m để phương trình có nghiệm không âm.
1) Phương trình ban đầu tương đương :
\(\left(2021x-2020\right)^3=\left(2x-2\right)^3+\left(2019x-2018\right)^3\)
Đặt \(a=2x-2,b=2019x-2018\)
\(\Rightarrow a+b=2021x-2020\)
Khi đó phương trình có dạng :
\(\left(a+b\right)^3=a^3+b^3\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow3\cdot\left(2x-2\right)\cdot\left(2019x-2018\right)\cdot\left(2021x-2002\right)=0\)
\(\Leftrightarrow\)Hoặc \(2x-2=0\)
Hoặc \(2019x-2018=0\)
Hoặc \(2021x-2020=0\)
\(\Rightarrow x\in\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\) (thỏa mãn)
Vậy : phương trình đã cho có tập nghiệm \(S=\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\)
\(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\)
\(\Leftrightarrow2x^2-3x+x^2-xm=3x^2+x-m\)
\(\Leftrightarrow-3x-xm=x-m\)
\(\Leftrightarrow4x+xm=m\Leftrightarrow x\left(4+m\right)=m\)
\(\Leftrightarrow x=\frac{m}{m+4}\)
Phương trình có nghiệm không âm \(\Leftrightarrow x\ge0\)
\(\Rightarrow\frac{m}{m+4}\ge0\)
Mà \(m+4>m\)nên \(\orbr{\begin{cases}m\ge0\\m+4\le0\end{cases}}\Leftrightarrow\orbr{\begin{cases}m\ge0\\m\le-4\end{cases}}\)























