Y=x3+2x2+5x+1
Những câu hỏi liên quan
Câu 1 : Thu Gọn Đa Thức P = x4 + x3 - x2 - x4 + 3x2 - 5x -1 ( khoanh tròn )
A. P = x4 + 2x2 - 5x -1 B. P = x3 - 2x2 -5x -1
C. P = x3 + 2x2 - 5x - 1 D. P = x3 + 2x2 + 5x - 1
giúp mik với
\(P=x^4+x^3-x^2-x^4+3x^2-5x-1.\)
\(\Leftrightarrow P=\left(x^4-x^4\right)+x^3+\left(3x^2-x^2\right)-5x-1\)
\(\Leftrightarrow P=x^3+2x^2-5x-1\)
Vậy chọn D
Hỏi hàm số y -1/3.x3 + 2x2 + 5x – 44 đồng biến trên khoảng nào? A. (-∞; -1). B. (-∞; 5) C. (5; +∞) D. (-1; 5).
Đọc tiếp
Hỏi hàm số y = -1/3.x3 + 2x2 + 5x – 44 đồng biến trên khoảng nào?
A. (-∞; -1).
B. (-∞; 5)
C. (5; +∞)
D. (-1; 5).
Đáp án D.
y’ = -x2 + 4x + 5
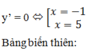
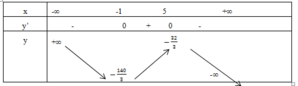
Vậy hàm số đồng biến trên khoảng (-1; 5)
Đúng 0
Bình luận (0)
Kết quả của phép tính ( x2 – 5x)(x + 3 ) là :
A. x3 – 2x2 – 15x
B. x3 + 2x2 + 15x
C. x3 + 2x2 – 15x
D. x3 – 2x2 + 15x
Đồ thị hàm số
y
x
3
+
2
x
2
+
5
x
+
1
và đường thẳng
y
3
x
+
1
cắt nhau tại điểm duy nhất
x
0
;
y
0
khi đó A.
y...
Đọc tiếp
Đồ thị hàm số y = x 3 + 2 x 2 + 5 x + 1 và đường thẳng y = 3 x + 1 cắt nhau tại điểm duy nhất x 0 ; y 0 khi đó
A. y 0 = − 2
B. y 0 = 1
C. y 0 = 0
D. y 0 = 3
Đáp án D
Hàm số đồng biến trên ℝ ⇔ hàm số có tập xác định D = ℝ và y ' ≥ 0 , ∀ x ∈ ℝ .
Đúng 0
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử
a) x3-2x2-5x+6
b) x4+5x2+6
c) x3+4x2+5x+2
d) x4+324
17 tháng 9 2023 lúc 14:07
Lời giải:
a. $=(x-y)(x+y)=[(-1)-(-3)][(-1)+(-3)]=2(-4)=-8$
b. $=3x^4-2xy^3+x^3y^2+3x^2y+12xy+15y-12xy-12$
$=3x^4-2xy^3+x^3y^2+3x^2y+15y-12$
=3-2.1(-2)^3+1^3.(-2)^2+3.1^2(-2)+15(-2)-12$
$=-25$
c.
$=2x^4+3x^3y-4x^3y-12xy+12xy=2x^4-x^3y$
$=x^3(2x-y)=(-1)^3[2(-1)-2]=-1.(-4)=4$
d.
$=2x^2y+4x^2-5xy^2-10x+3xy^2-3x^2y$
$=(2x^2y-3x^2y)+4x^2+(-5xy^2+3xy^2)-10x$
$=-x^2y+4x^2-2xy^2-10x$
$=-3^2.(-2)+4.3^2-2.3(-2)^2-10.3=0$
Đúng 1
Bình luận (0)
Bài 1: Thực hiện phép tính:
a) (2x4-x3 5x-6x2-1):(1-2x)
b)(x3-3x2 3x-2):(x2-x 1)
c) (2x3 5x2-2x 3):(2x2-x 1)
d)\(\dfrac{5x y^2}{x^2y}\) \(\dfrac{5y-x^2}{xy^2}\)
e)\(\dfrac{27-x^3}{5x 5}\):\(\dfrac{2x-6}{3x 3}\)
f)\(\dfrac{x 2}{4x 24}\).\(\dfrac...
Xem chi tiết
27 tháng 4 2023 lúc 23:26
Tính.
a, (x3-2x2-10x-7):(x2-7-3x)
b, (x3+4x2+8x+5):(x+1)
c, (x3-x2-13x-14):(x2-3x-7)
d, (x3+5x2+5x):(x+5)
a: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)
b:\(=\dfrac{x^3+x^2+3x^2+3x+5x+5}{x+1}=x^2+3x+5\)
c:\(=\dfrac{x^3-3x^2-7x+2x^2-6x-14}{x^2-3x-7}=x+2\)
d: \(=\dfrac{x^2\left(x+5\right)+5x+25-25}{x+5}=x^2+5-\dfrac{25}{x+5}\)
Đúng 1
Bình luận (0)
Thực hiện phép tính:
a)(x4-3x-1):(x2-x-1)
b)(x3-x2+5x-4):(-x+2x2+1)
c)(2x2+2x-5x3+2x4-1):(-x+x2+1)
\(a,=\left[x^2\left(x^2-x-1\right)+x^3+x^2-3x-1\right]:\left(x^2-x-1\right)\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2x^2-2x-1\right]\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)\\ =\left[\left(x^2+x+2\right)\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)=x^2+x+2R1\)
Đúng 2
Bình luận (0)
Thực hiện phép chia:a) (
x
3
-
2
x
2
- 15x + 36) : (x + 4);b) (
2
x
4
+
2
x
3
+
3
x
2
- 5x - 20) : (
x
2
+ x + 4);c) (2
x
3...
Đọc tiếp
Thực hiện phép chia:
a) ( x 3 - 2 x 2 - 15x + 36) : (x + 4);
b) ( 2 x 4 + 2 x 3 + 3 x 2 - 5x - 20) : ( x 2 + x + 4);
c) (2 x 3 + 11 x 2 + 18x-3) : (2x + 3);
d) (2x3 + 9x2 +5x + 41) : (2x2 - x + 9).
a) Đa thức thương x 2 – 6x + 9.
b) Đa thức thương 2 x 2 – 5.
c) Đa thức thương x 2 + 4x + 3 và đa thức dư -12.
d) Đa thức x + 5 và đa thức dư x – 4.
Đúng 0
Bình luận (0)