cho biet: 10a2-3b2+ab=0; b>a>0
chứng minh: \(\frac{2a-b}{3a-b}+\frac{5b-a}{3a+b}=9:5\)
Những câu hỏi liên quan
Cho a,b là các số thực dương thỏa mãn a2 -2ab -3b2 ≥ 0. Tìm giá trị nhỏ nhất P =\(\dfrac{4a^2+b^2}{ab}\)
Lời giải:
$a^2-2ab-3b^2\geq 0$
$\Leftrightarrow (a^2+ab)-(3ab+3b^2)\geq 0$
$\Leftrightarrow a(a+b)-3b(a+b)\geq 0$
$\Leftrightarrow (a+b)(a-3b)\geq 0$
$\Leftrightarrow a-3b\geq 0$ (do $a+b>0$ với mọi $a,b>0$)
$\Leftrightarrow a\geq 3b$
Xét hiệu:
$P-\frac{37}{3}=\frac{4a^2+b^2}{ab}-\frac{37}{3}$
$=\frac{12a^2+3b^2-37ab}{3ab}=\frac{(a-3b)(12a-b)}{3ab}\geq 0$ do $a\geq 3b>0$
$\Rightarrow P\geq \frac{37}{3}$
Vậy $P_{\min}=\frac{37}{3}$
Đúng 1
Bình luận (0)
Cho y
x
cos
2
x
trên
-
π
2
;
π
2
và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) 0. Biết
a
∈
-...
Đọc tiếp
Cho y = x cos 2 x trên - π 2 ; π 2 và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) = 0. Biết a ∈ - π 2 ; π 2 thỏa mãn tan a = 3. Tính F(a) – 10a2 + 3a
A. 1 2 ln 10
B. - 1 4 ln 10
C. - 1 2 ln 10
D. ln 10
Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
=> 
Đúng 0
Bình luận (0)
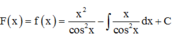
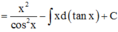
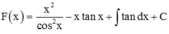
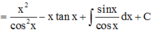
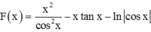
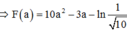
Cho biểu thức:
P=\(\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\)
a) rút gọn P
b) có giá trị nào của a,b để P=0
c) tính giá trị của P biết a,b thỏa mãn điều kiện: 3a2+3b2= 10ab và a>b>0
\(P=\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\) (\(a\ne b;a\ne0;a\ne-b;b\ne0\))
\(=\dfrac{a^2}{b\left(a+b\right)}+\dfrac{b^2}{a\left(b-a\right)}-\dfrac{a^2+b^2}{ab}\)
\(=\dfrac{a^3\left(a-b\right)-b^3\left(a+b\right)-\left(a^2+b^2\right)\left(a+b\right)\left(a-b\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^2+b^2\right)\left(a^2-b^2\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^4-b^4\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-a^3b-b^3a}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-ab\left(a^2+b^2\right)}{ab\left(a+b\right)\left(a-b\right)}=-\dfrac{a^2+b^2}{a^2-b^2}\).
b) -Ta có: \(P=0\)
\(\Leftrightarrow-\dfrac{a^2+b^2}{a^2-b^2}=0\)
\(\Leftrightarrow a^2+b^2=0\)
-Vì \(a^2\ge0;b^2\ge0\)
\(\Rightarrow a=0;b=0\) (không thỏa mãn điều kiện).
-Vậy không có giá trị nào của a,b để \(P=0\).
c)
Đúng 1
Bình luận (0)
Chứng minh rằng nếu a,b,c > 0 thoả mãn a+b+c = 3 thì ab+a 3b2+10b+3 + bc+b 3c2+10c+3 + ca+c 3a2+10a+3 ≥
3 8
Cho 3 a 2 + 3 b 2 = 10 a b và b > a > 0. Tính giá trị của biểu thức P = a - b a + b
27 tháng 6 2021 lúc 15:58
các bạn giúp mình bài này với
cho các số thực dương a,b,c thỏa mãn điều kiện ab+bc+ca=1.CMR:10a2+10b2+c2 >hoặc= 4
thanks trước
Áp dụng AM-GM có:
\(2a^2+2b^2\ge4ab\)
\(8b^2+\dfrac{1}{2}c^2\ge4bc\)
\(8a^2+\dfrac{1}{2}c^2\ge4ac\)
Cộng vế với vế \(\Rightarrow VT\ge4\left(ab+bc+ac\right)=4\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}ab+bc+ac=1\\a=b=\dfrac{c}{4}\end{matrix}\right.\)\(\Rightarrow a=b=\dfrac{1}{3};c=\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
Cho 4a2-15ab+3b2=0,b≠4a, b≠-4a. Tính giá trị của biểu thức:T=\(\dfrac{5a-b}{4a-b}\)+\(\dfrac{3b-2a}{4a+b}\)
cho a và b lần lượt thỏa mãn các hệ thức sau
a3-3a2+5a-2020=0 và b3-3b2=5b=2014
tính a+b
Thu gọn các phân thức sau: a)
b
2
+
2
b
+
1
3
b
3
+
3
b
2
với
b
≠
−
1
và
b
≠
0
;...
Đọc tiếp
Thu gọn các phân thức sau:
a) b 2 + 2 b + 1 3 b 3 + 3 b 2 với b ≠ − 1 và b ≠ 0 ;
b) 9 u 2 v 2 + 3 u 2 12 uv 5 + 4 uv 3 với u ≠ 0 và v ≠ 0
a) Rút gọn được b + 1 3 b 2 ; b) Rút gọn được 3 u 4 v 3 .
Đúng 0
Bình luận (0)
cho a,b,c thoả a3 + b3 + c3 = 3abc và a,b,c khác 0. Chứng minh rằng biểu thức Q = a2+ 3b2 + 5c2 / (a + b + c)2 có giá trị không đổi
