Các câu hỏi tương tự
Bài 1: Cho xyz=2 và x+y+z=0. Tính giá trị của biểu thức: N=(x+y)(y+z)(x+z)
Bài 2: Tính giá trị biểu thức: 3a-2b / a-3b với a/b= 10/3
Bài 5: Tính giá trị của biểu thức: a-8 / b-5 - 4a-b / 3a+3 với a-b=3
a) Tìm giá trị nhỏ nhất của biểu thức \(x^2-8x+5\)
b) Cho \(a^3+b^3+c^3=3abc\) và \(a+b+c\) ≠ 0
Tính giá trị của biểu thức N =\(\dfrac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\)
Cho a,b > 0 và a+b=a^2+b^2=a^3+b^3
tính giá trị của biểu thức : P = a^2011+b^2015
Cho a>0, b>0, ab= 3, a2 + b2 =10. Tính giá trị của biểu thức:
B= 16/( a2 - b2 )
tính giá trị của biểu thức a) cho a+b=5 ab=6 tính a^3+b^3
b)cho a+b=1 tính giá trị của 2.(a^3+b^3)-3.(a^2+b^2)
Cho a3+b3+c3 =3abc và a+b+c khác 0.Tính giá trị biểu thức N=\(\frac{a^2+b^2+c^2}{\left(a+b+a\right)^2}\)
Cho a+b=1.Tính giá trị của biểu thức sau M= a3+b3+3ab(a2+b2)+6a2b2(a+b)
Giúp mk vs nha!!Thanks mn nhìuu:))))
Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.
a) Tính giá trị của biểu thức A khi x = 2/3.
b) Chứng minh B = x−1/x .
c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.
Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.
a) Tính giá trị của biểu thức A khi x = 2/3.
b) Chứng minh B = x−1/x .
c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.
a. Cho a+b=3. Tìm giá trị nhỏ nhất của a^2 + b^2.
b. Cho 1/x^2 + x^2=14 (x<>0). Tính giá trị của biểu thức 1/x^3 + x^3
Cho a,b>0 và a+b=a2+b+2=a3+b3
Tính giá trị của biểu thức P=a2011+b2018




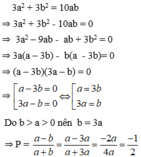



![❄Đờ[̲̅i̲̅]❤Là❤Bể❤K[̲̅h̲̅...](https://hoc24.vn/images/avt/avt2782456_256by256.jpg)




