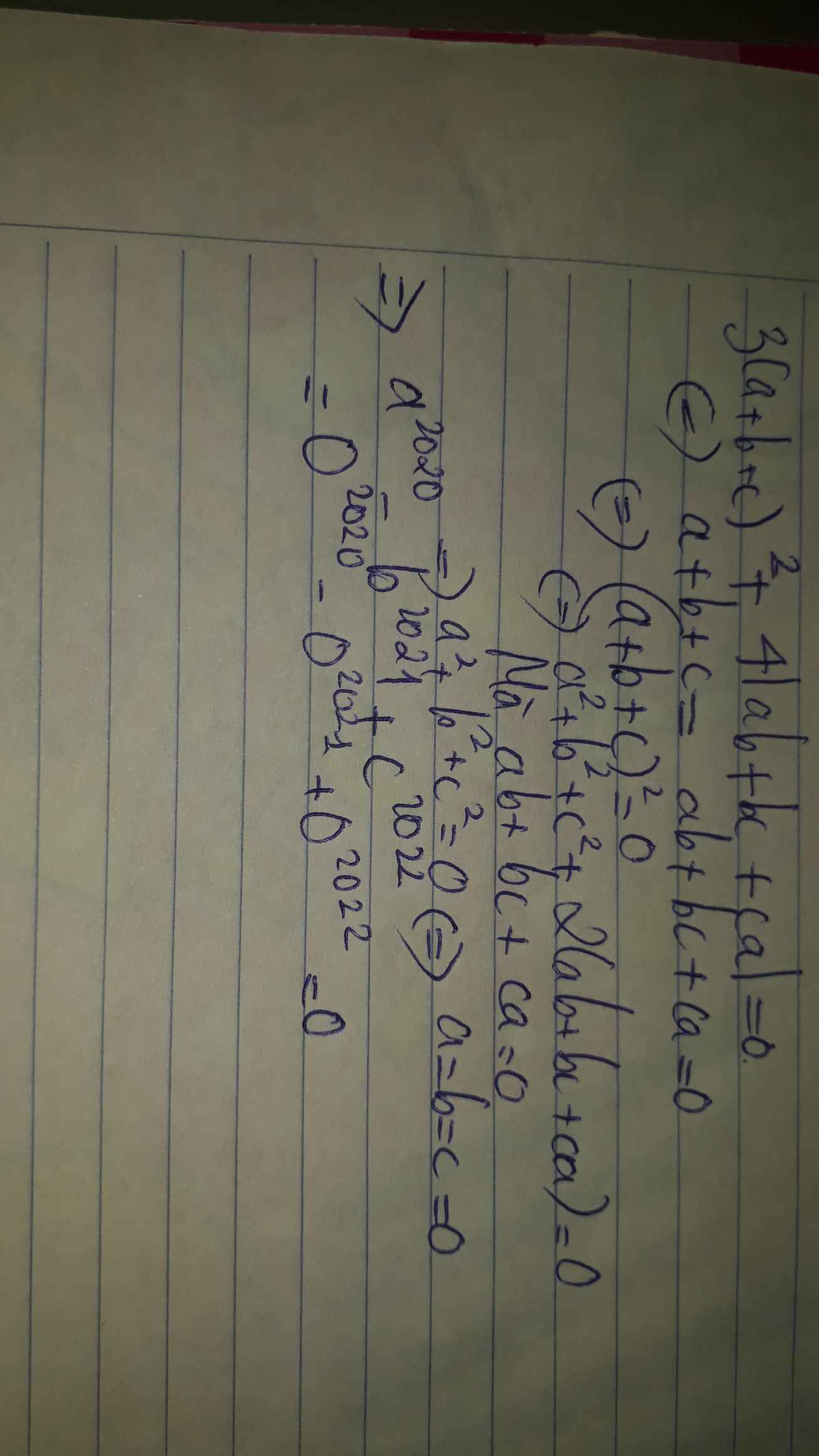\(=\left(2022-2020\right)+\left(2018-2016\right)+...+\left(6-4\right)+2=2+2+...+2=506.2=1012\)

a, S=1+(-2)+3+(-4)+...+199+(-200)

    S=[1+(-2)]+[3+(-4)]+...+[199+(-200)]

    S=-1+(-1)+...+(-1)     (có 100 số -1)

    S=-1.100

    S=-100  

b,M=(-2)+4+(-6)+8+...+(-2018)+2020+(-2022)

   M=(-2+4)+(-6+8)+...+(-2018+2020)+(-2022)

   M=2+2+...+2+(-2022)   (có 505 số 2)

   M=2.505-2022

   M=1010-2022

   M=-1012

a) S = 1+(-2)+3+(-4)+....+199+(-200)

    S = 1 - 2 +3 -4 +.....+199-200

A = 1 + 3 +.....+ 199

SSH của A là : ( 199 - 1) : 2 +1= 100 (số)

Tổng của A là : ( 199 + 1) .100 : 2 = 10000

B = 2 + 4 +....+200

SSH của B là: ( 200 - 2) : 2+1 = 100 (số)

Tổng của B là: (200 + 2) .100 : 2 = 10100

 Vậy A - B = 10000 - 10100 = -100

b) M = (-2) + 4 +(-6) + 8+...+ (-2018) + 2020+ (-2022)

    M = -2 + 4 -6 + 8 + ....-2018 + 2020 -2022

 A = 2 + 6 + ....+2018 + 2022

SSH của A là : ( 2022 - 2 ) : 4+1 =506(số)

Tổng của A là: ( 2022+2) .505 : 2 = 512072

B = 4 + 8 +...+2020

SSH của B là : (2020 -4) : 4 +1 = 505(số)

Tổng của B là : ( 2020 +4) . 505 : 2 = 511060

 Vậy A - B = 512072 - 511060 = 1012

\(\left(x-6\right)^{2020}+2\left(y-3\right)^{2020}=0\)

Ta có : \(\left(x-6\right)^{2020}\ge0\forall x\)

            \(2\left(y+3\right)^{2020}\ge0\forall y\)

        =>\(\left(x-6\right)^{2020}+2\left(y+3\right)^{2020}\ge0\forall x,y\)

Dấu "=" xảy ra <=>\(\left\{{}\begin{matrix}x-6=0\\y+3=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=6\\y=-3\end{matrix}\right.\)

\(a^{2019}+b^{2019}=a^{2020}+b^{2020}\\ \Leftrightarrow a^{2020}-a^{2019}=b^{2019}-b^{2020}=0\\ \Leftrightarrow a^{2019}\left(a-1\right)=b^{2019}\left(1-b\right)\\ \Leftrightarrow\dfrac{a^{2019}}{b^{2019}}=\dfrac{1-b}{a-1}\left(1\right)\\ a^{2020}+b^{2020}=a^{2021}+b^{2021}\\ \Leftrightarrow a^{2021}-a^{2020}=b^{2020}-b^{2021}\\ \Leftrightarrow a^{2020}\left(a-1\right)=b^{2020}\left(1-b\right)\\ \Leftrightarrow\dfrac{a^{2020}}{b^{2020}}=\dfrac{1-b}{a-1}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\dfrac{a^{2019}}{b^{2019}}=\dfrac{a^{2020}}{b^{2020}}\Leftrightarrow\dfrac{a}{b}=1\Leftrightarrow a=b\\ \Leftrightarrow2a^{2019}=2a^{2020}\\ \Leftrightarrow a=1=b\\ \Leftrightarrow P=2022-\left(1+1-1\right)^{2022}=2021\)

Ta có: \(3\left(a+b+c\right)^2\ge0\forall a,b,c\)

\(4\left|ab+bc+ca\right|\ge0\forall a,b,c\)

Do đó: \(3\left(a+b+c\right)^2+4\left|ab+bc+ca\right|\ge0\forall a,b,c\)

Dấu '=' xảy ra khi a=b=c=0

Ta có: \(a^{2020}-b^{2021}+c^{2022}\)

\(=0^{2020}-0^{2021}+0^{2022}\)

=0

Cứu với ;-;

=1+(2-3-4+5)+(6-7-8+9)+.....+(2018-2019-2020+2021)+2022

=1+0+0+.....+0+2022

=2023

số năm nay luôn

Ta có: 1+2-3-4+5+6-7-8+.....-2019-2020+2021+2022

=1+(2-3-4+5)+(6-7-8+9)+.....+(2018-2019-2020+2021)+2022

=1+0+0+.....+0+2022

=2023