Tam giác ABC vuông tại A, đường cao AH. Biết AH=6cm, CH=8cm. Tính AC, BC, AB và góc CAH

Những câu hỏi liên quan
a) Cho ∆ABC vuông tại A có đường cao AH. Biết AH = 6cm , HC = 8cm. Tính AC, BC, AB và số đo góc CAH ( làm tròn đến độ )
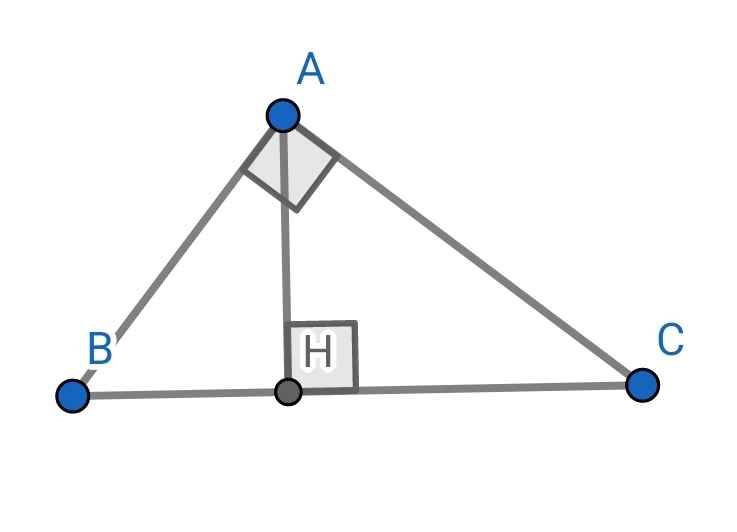 ∆ABC vuông tại A có AH là đường cao
∆ABC vuông tại A có AH là đường cao
⇒ AH² = HB.HC
⇒ HB = AH² : HC
= 6² : 8
= 4,5 (cm)
⇒ BC = HB + HC
= 4,5 + 8
= 12,5 (cm)
∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
= 6² + 4,5²
= 56,25
⇒ AB = 7,5 (cm)
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
⇒ AC² = BC² - AB²
= 12,5² - 7,5²
= 100
⇒ AC = 10 (cm)
sinCAH = HC/AC
= 8/10
= 0,8
⇒ CAH ≈ 53⁰
Đúng 1
Bình luận (0)
HB=6^2/8=4,5cm
AB=căn 4,5*12,5=7,5cm
AC=cân 8*12,5=10cm
góc CAH=góc B
sin B=AC/BC=10/12,5=4/5
=>góc CAH=53 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH; biết AB = 6cm, AC = 8cm a) Tính BC, AH b) Từ H kẻ HM và HN lần lượt vuông góc với AB và AC. Tính MN
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
b: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
=>MN=AH
mà AH=4,8cm
nên MN=4,8cm
Đúng 1
Bình luận (0)
a) Để tính BC, ta sử dụng định lý Pythagoras trong tam giác vuông ABC:
BC^2 = AB^2 + AC^2
BC^2 = 6^2 + 8^2
BC^2 = 36 + 64
BC^2 = 100
BC = √100
BC = 10 cm
Để tính AH, ta sử dụng công thức diện tích của tam giác:
S = 1/2 * AB * AH
S = 1/2 * 6 * AH
S = 3AH
Vì tam giác ABC là tam giác vuông, nên diện tích tam giác ABC cũng có thể tính bằng cách sử dụng công thức diện tích tam giác vuông:
S = 1/2 * AB * AC
S = 1/2 * 6 * 8
S = 24
Vậy, ta có phương trình:
3AH = 24
AH = 8 cm
b) Để tính MN, ta sử dụng tỷ lệ giữa các đoạn thẳng trong tam giác đồng dạng. Ta có:
MN/BC = HM/AB = HN/AC
Vì HM và HN là đường cao của tam giác ABC, nên ta có:
HM = AH = 8 cm
HN = AH = 8 cm
Vậy, ta có:
MN/10 = 8/6
MN = (8/6) * 10
MN = 80/6
MN ≈ 13.33 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng AB=6cm và AC=8cm. Tính độ dài AH, BH, CH, và BC.
Diện tích tam giác ABC là:
6.8:2=24 (cm2)
Áp dụng định lí Py-ta-go cho tam giác ABC, ta có:
AB2+AC2=BC2
=>62+82=BC2=>36+64=BC2=>BC=10 (cm)
Đường cao AH dài là:
24.2:10=4,8 (cm)
Áp dụng định lí Py-ta-go cho tam giác ABH, ta có:
AH2+BH2=AB2
=>4,82+BH2=36
=>23,04+BH2=36
=>BH2=12,96=>BH=3,6 (cm)
Độ dài CH là:
10-3,6=6,4 (cm)
Đáp số: AH: 4,8 cm; BH: 3,6 cm; CH: 6,4 cm; BC: 10 cm
\(\text{Áp dụng định lý Pytago ta có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=6^2+8^2\)
\(\Rightarrow BC^2=100\)
\(\Rightarrow BC=10\left(\text{Vì BC}>0\right)\)
\(S_{\Delta ABC}\text{ là}:\)
\(\frac{6.8}{2}=24\)
\(\text{Vì AH là đường cao hạ từ đỉnh A và BC là đáy tương ứng với đường cao AH nên}\)
\(S_{\Delta ABC}=\frac{BC.AH}{2}=\frac{10.AH}{2}=24\)
\(\Rightarrow AH=24:5=4,8\)
\(\text{Áp dụng định lý Pytago ta có:}\)
\(AB^2=AH^2+BH^2\)
\(\Rightarrow6^2=4,8^2+BH^2\)
\(BH^2=12.96\)
\(BH=3,6\)
\(\text{CH thì tính tương tự như BH nha}\)
cho tam giác abc vuông tại a , đường cao ah ab=6cm ac=8cm. a) tính bc,ah,bh,ch b) kẻ ie và if lần lượt vuông góc với ab và ac .cm hb .hc=ea.eb+fa.fc
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
b) Kẻ HE,HF vuông góc với AB,AC chớ,chứ ko có điểm I
Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow EF=AH\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow EA.EB=EH^2\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow FA.FC=HF^2\Rightarrow EA.EB+FA.FC=EH^2+FH^2=EF^2=AH^2\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\Rightarrow HB.HC=EA.EB+FA.FC\)
Đúng 3
Bình luận (0)
Tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, AC = 8cm. Tính BC, AH, BH, Tính góc C làm tròn đến độ
Vì ▲ABC vuông tại A nên: BC2 = AB2 + AC2(Định lý Pytago)
⇔ BC = \(\sqrt{^{ }AB^2+AC^2}\)
= \(\sqrt{6^2+8^2}\)
= \(\sqrt{36+64}\)
= \(\sqrt{100}\) = 10(cm)
+) 2SABC = AB . AC = BC . AH ⇔ AH = \(\dfrac{AB.AC}{BC}\)
= \(\dfrac{6.8}{10}\)
= 4,8(cm)
➤ BC = 10 cm và AH = 4,8 cm
Đúng 0
Bình luận (0)
Câu hỏi không thể chấp nhận được. Cậu tự giải tiếp đi.
Đúng 0
Bình luận (0)
ai biết giải giúp minh với:Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minha,tứ giác HECD nội tiếpb,Tia DA là tia phân giác góc EDK Cây 2:cho tam giác ABC vuông tai A,biết ab6cm,ac8cmA.tính bcB,kẻ đường cao AH,tính Ah Câu 3:Cho tam giác abc vuông tại A,BIẾT AC4cm,Bc5cm.A,Tính cạnh ABB,kẻ đường cao AH,TÍNH AHCâu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB12CM,AC5CM.tính BH,CHCâu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC18cm,B...
Đọc tiếp
ai biết giải giúp minh với:
Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minh
a,tứ giác HECD nội tiếp
b,Tia DA là tia phân giác góc EDK
Cây 2:cho tam giác ABC vuông tai A,biết ab=6cm,ac=8cm
A.tính bc
B,kẻ đường cao AH,tính Ah
Câu 3:Cho tam giác abc vuông tại A,BIẾT AC=4cm,Bc=5cm.
A,Tính cạnh AB
B,kẻ đường cao AH,TÍNH AH
Câu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB=12CM,AC=5CM.tính BH,CH
Câu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC=18cm,BH=6cm.Tính độ dài các cạnh AB,AC
Cau 6:Cho tam giác ABC,vuông tại A,biết AB=4cm,đường cao AH=2CM,tính các góc và các cạnh còn lại cua tam giac.?
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
Đúng 1
Bình luận (0)
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm. AC=8cm a) Tính BC,AH, góc B,góc C b) Vẽ AM là đường trung tuyến của tam giác ABC (M thuộc BC) . Chứng minh góc BAH= góc MAC c) Vẻ HE vuông góc AB (E thuộc AB), HF vuông góc AC (F thuộc AC) . Chứng minh EF vuông góc AM tại K và tính độ dài AK
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB=BC/2
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\left(1\right)\)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAB}+\widehat{ABH}=90^0\)(ΔABH vuông tại H)
Do đó: \(\widehat{ACB}=\widehat{HAB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAC}=\widehat{HAB}\)
c: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AFE}=\widehat{ABC}\)
\(\widehat{AFE}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>FE vuông góc AM tại K
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(HA^2=AE\cdot AB\)
=>\(AE\cdot6=4,8^2\)
=>\(AE=3,84\left(cm\right)\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
=>\(AF=\dfrac{4.8^2}{8}=2,88\left(cm\right)\)
Xét ΔAEF vuông tại A có AK là đường cao
nên \(\dfrac{1}{AK^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
=>\(\dfrac{1}{AK^2}=\dfrac{1}{2,88^2}+\dfrac{1}{3.84^2}\)
=>AK=2,304(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm, AC=8cm, BC=10cm. Tính AH
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
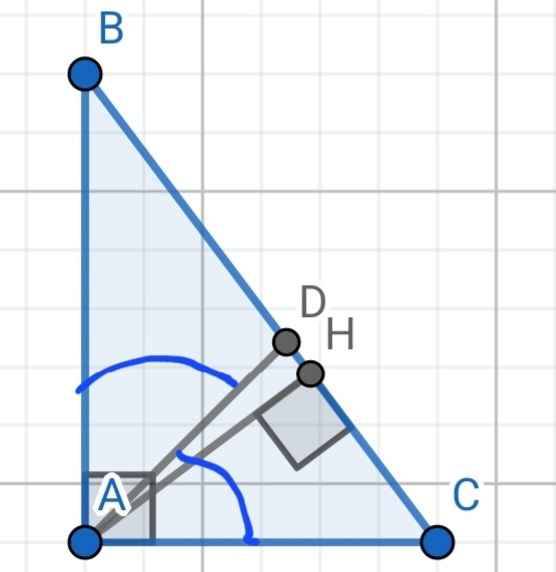
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
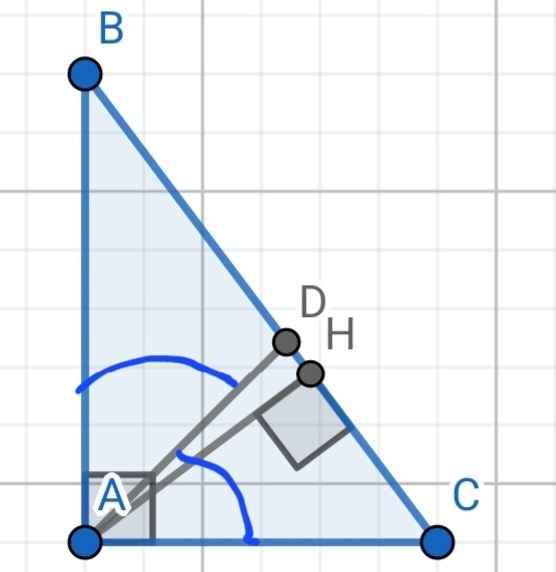
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
Đúng 1
Bình luận (0)
a: DB/DC=AB/AC=4/3
b: Sửa đề: AH/CA=AB/BC
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>AH*BC=AB*AC
=>AH/AC=AB/CB
Đúng 0
Bình luận (0)

























