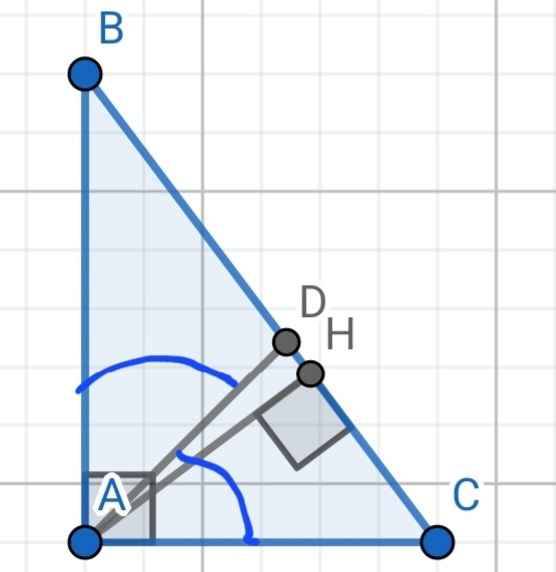
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA

a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
Cho tam giác ABC vuông tại A ( AC > AB ), đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Qua D kẻ đường thẳng vuông góc với BC, cắt cạnh AC tại E.
a) Chứng minh tam giác ABC đồng dạng với tam giác HAC
b) Chứng minh EC . AC = DC. BC
c) Chứng minh tam giác BEC = tam giác ADC và tam giác ABE vuông cân
Cho tam giác ABC vuông tại A , biết AB=12cm , AC= 16cm kẻ AH vuông góc với BC ( H thuộc BC)
a. chứng minh tam giác ABC đồng dạng với tam giác HBA
b.tính BC, AH , HB
c. Kẻ đường phân giác BD , tính AD/CD
Cho Tam giác ABC vuông tại A có AB=9cm, AC=12cm , đường cao AH a) chứng minh: tam giác abh ~ tam giác cba b) tính BC;AH c) Tia phân giác góc B cắt AC tại D.Chứng minh: AD.AC=AH.DC
Cho tam giác ABC nhọn (AB<AC). Gọi AH là đường cao. Kẻ HM⊥AB tại M, HN⊥AC tại N.
a) Chứng minh ΔAHM đồng dạng ΔABH.
b) AH=8cm, B=6cm. Tính AM.
c) Trên tia đối tia NM lấy điểm E sao cho góc AEN= góc ACE. Chứng minh ΔAHE cân
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH (H ∈ BC).
a) Chứng minh : AABC dồng dạng với AHBA.
b) Lấy điểm M thuộc AH. Kẻ đường thẳng đi qua B và vuông góc với CM tại K. Chứng minh : CM.CK = CH.CB.
c) Tia BK cắt HA tại D. Chứng minh: BKH = BCD.
giúp mình câu c với ạ!