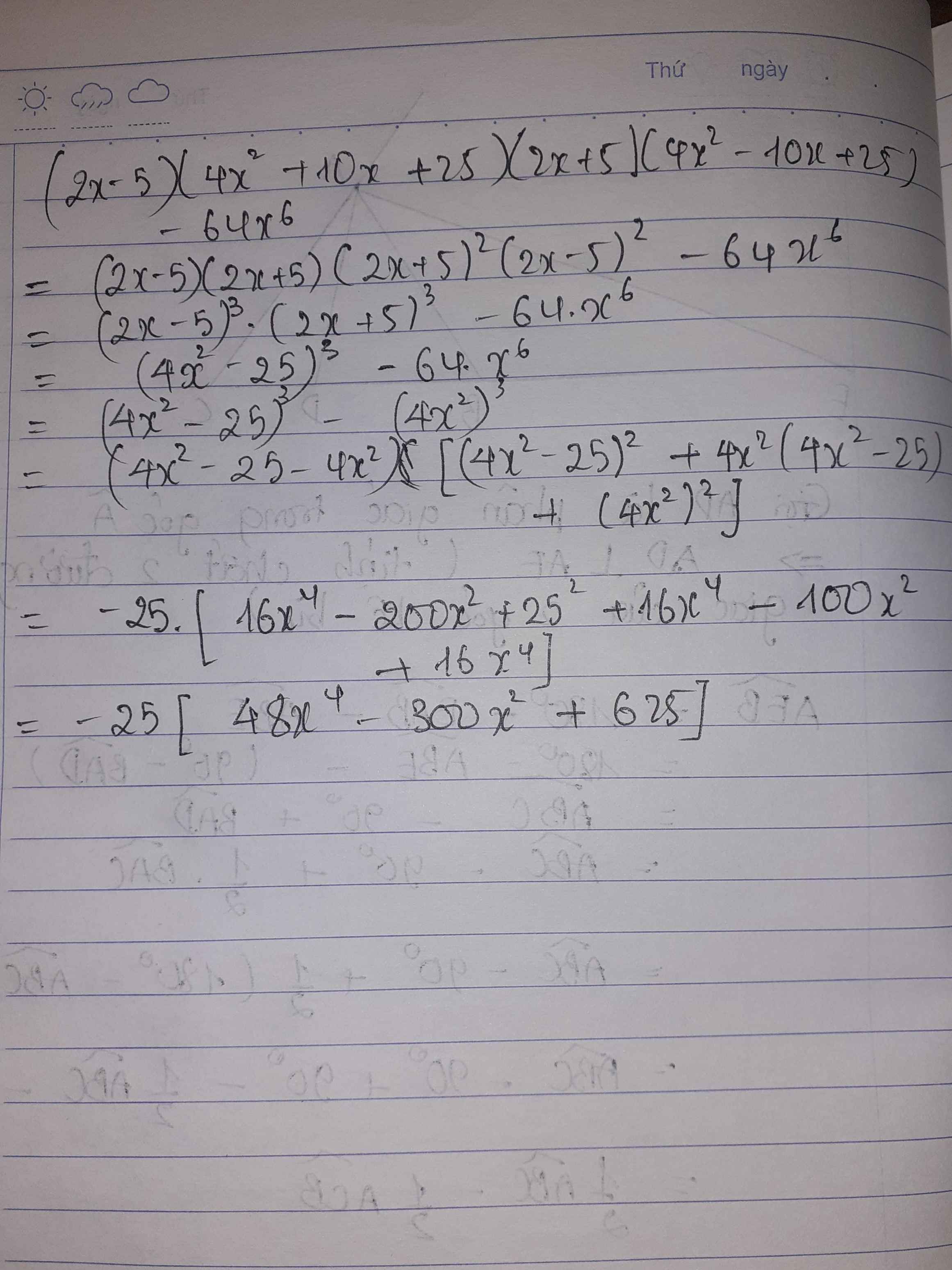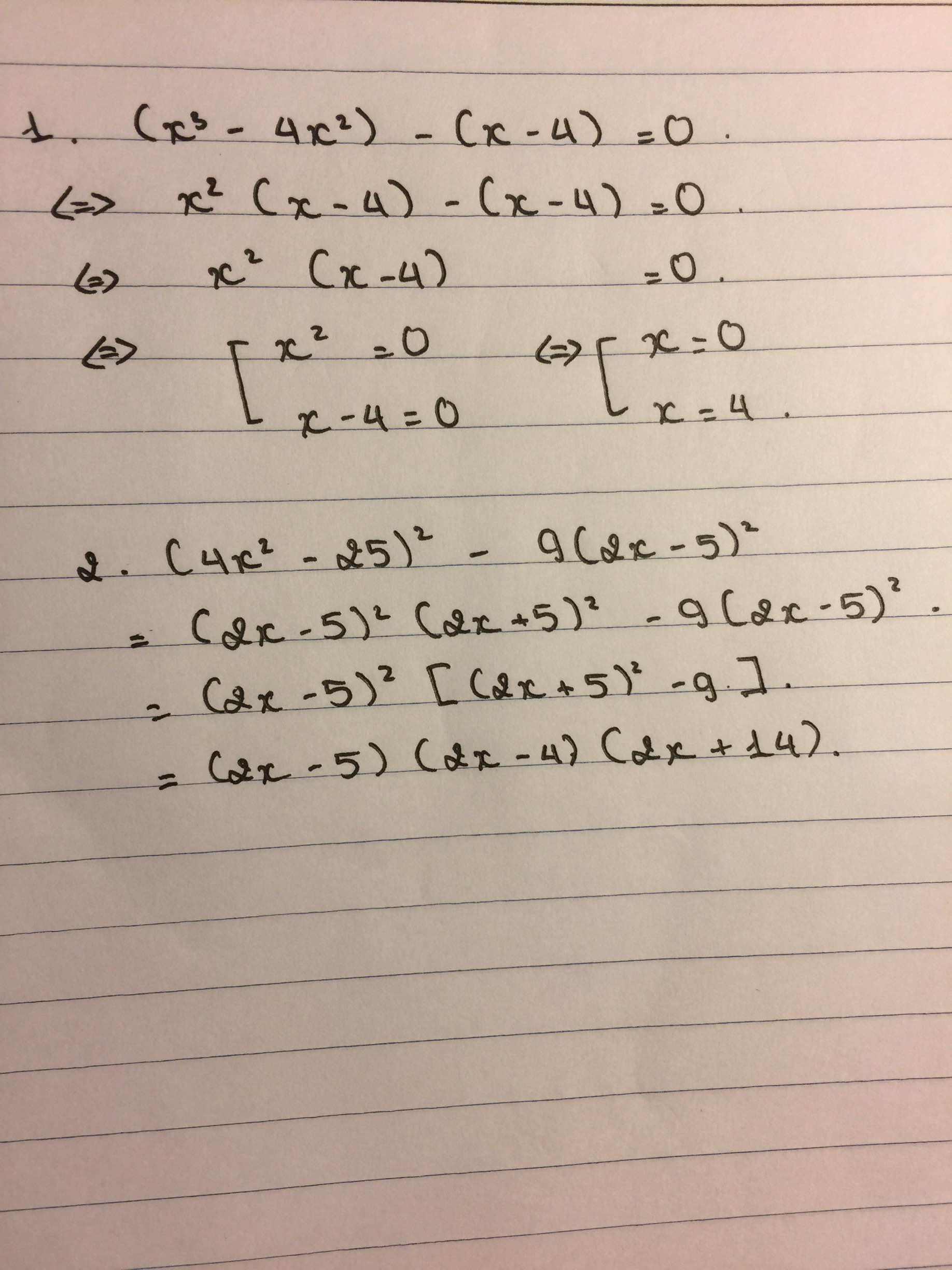g) \(4x^2-25-\left(2x-5\right)\left(2x+7\right)=0\)

  \(\Rightarrow\left(2x-5\right)\left(2x+5\right)-\left(2x-5\right)\left(2x+7\right)=0\)

  \(\Rightarrow\left(2x-5\right)\left(2x+5-2x-7\right)=0\)

  \(\Rightarrow-2\left(2x-5\right)=0\Rightarrow x=\dfrac{5}{2}\)

i) \(x^3+27+\left(x+3\right)\left(x-9\right)=0\)

  \(\Rightarrow\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)=0\)

  \(\Rightarrow\left(x+3\right)\left(x^2-3x+9+x-9\right)=0\)

  \(\Rightarrow\left(x+3\right)\left(x^2-2x\right)=0\Rightarrow x\left(x+3\right)\left(x-2\right)=0\)

  \(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=2\end{matrix}\right.\)

Ta có: \(\left(2x-5\right)\left(4x^2+10x+25\right)\left(2x+5\right)\left(4x^2-10x+25\right)-64x^6\)

\(=\left(8x^3-125\right)\left(8x^3+125\right)-64x^6\)

\(=64x^6-15625-64x^6\)

=-15625

\(\left(5-2x\right)\left(2x+7\right)=4x^2-25\)

\(\Leftrightarrow-\left(2x-5\right)\left(2x+7\right)=\left(2x-5\right)\left(2x+5\right)\)

\(\Leftrightarrow-2x-7=2x+5\)

\(\Leftrightarrow-4x=12\Leftrightarrow x=-3\)

\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)

\(\Leftrightarrow\left[2\left(2x+7\right)\right]^2-\left[3\left(x+3\right)\right]^2=0\)

\(\Leftrightarrow\left[2\left(2x+7\right)-3\left(x+3\right)\right].\left[2\left(2x+7\right)+3\left(x+3\right)\right]=0\)

\(\Leftrightarrow\left(4x+14-3x-9\right)\left(4x+14+3x+9\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(7x+23\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\7x+23=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\frac{23}{7}\end{matrix}\right.\)

b/\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)

\(\Leftrightarrow4\left(4x^2+28x+49\right)-9\left(x^2+6x+9\right)=0\)

\(\Leftrightarrow16x^2+112x+196-9x^2-36x-81=0\)

\(\Leftrightarrow7x^2+76x+115=0\)

\(\Leftrightarrow x=\frac{-38\pm3\sqrt{71}}{7}\)

Vậy ..

Lời giải:
a) $|4x^2-25|=0$

$\Leftrightarrow 4x^2-25=0$

$\Leftrightarrow (2x-5)(2x+5)=0$

$\Rightarrow x=\pm \frac{5}{2}$

b) 

$|x-2|=3$

\(\Rightarrow \left[\begin{matrix} x-2=-3\\ x-2=3\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-1\\ x=5\end{matrix}\right.\)

c) 

\(|x-3|=2x-1\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ \left[\begin{matrix} x-3=2x-1\\ x-3=1-2x\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\end{matrix}\right.\Rightarrow x=\frac{4}{3}\)

d) 

$|x-5|=|3x-2|$

\(\Rightarrow \left[\begin{matrix} x-5=3x-2\\ x-5=2-3x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)

1: Ta có: \(\left(x^3-4x^2\right)-\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\\x=-1\end{matrix}\right.\)

1, \(\left(x-1\right)\left(x+2\right)-\left(x-1\right)^2=0\)

\(\Leftrightarrow\left(x-1\right)\left[x+2-\left(x-1\right)\right]=0\)

\(\Leftrightarrow3\left(x-1\right)=0\Leftrightarrow x=1\)

2, \(\left(x-2\right)^2-3\left(x-2\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left[x-2-3\left(x+1\right)\right]=0\)

\(\Leftrightarrow\left(x-2\right)\left(-2x-5\right)=0\Leftrightarrow x=-\dfrac{5}{2};x=2\)

3, \(\left(5-2x\right)\left(2x+7\right)=4x^2-25=\left(2x-5\right)\left(2x+5\right)\)

\(\Leftrightarrow\left(5-2x\right)\left(2x+7\right)+\left(5-2x\right)\left(2x+5\right)=0\)

\(\Leftrightarrow\left(5-2x\right)\left(2x+7+2x+5\right)=0\Leftrightarrow\left(4x+12\right)\left(5-2x\right)=0\Leftrightarrow x=-3;x=\dfrac{5}{2}\)

1) Ta có: \(\left(x-1\right)\left(x+2\right)-\left(x-1\right)^2=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+2-x+1\right)=0\)

\(\Leftrightarrow x-1=0\)

hay x=1

2) Ta có: \(\left(x-2\right)^2-3\left(x-2\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-2-3x-3\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(-2x-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-5}{2}\end{matrix}\right.\)

a) \(\left|4x^2-25\right|=0\)

\(\Leftrightarrow4x^2-25=0\)

\(\Leftrightarrow\left(2x+5\right)\left(2x-5\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}2x-5=0\\2x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{5}{2}\end{cases}}}\)

c: Ta có: \(\left(x+3\right)^3-x\left(3x+1\right)^2+\left(2x+1\right)\left(4x^2-2x+1\right)=28\)

\(\Leftrightarrow x^3+9x^2+27x+27-9x^3-6x^2-x+8x^3+1=28\)

\(\Leftrightarrow3x^2+26x=0\)

\(\Leftrightarrow x\left(3x+26\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{26}{3}\end{matrix}\right.\)

\(a,\Leftrightarrow x^2+8x+16-x^3-12x^2=16\\ \Leftrightarrow x^3+11x^2-8x=0\\ \Leftrightarrow x\left(x^2+11x-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+11x-8=0\left(1\right)\end{matrix}\right.\\ \Delta\left(1\right)=121+32=153\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-11-3\sqrt{17}}{2}\\x=\dfrac{-11+3\sqrt{17}}{2}\end{matrix}\right.\\ S=\left\{0;\dfrac{-11-3\sqrt{17}}{2};\dfrac{-11+3\sqrt{17}}{2}\right\}\)

\(c,\Leftrightarrow x^3+9x^2+27x+27-9x^3-6x^2-x+8x^3+1=28\\ \Leftrightarrow3x^2+26x=0\\ \Leftrightarrow x\left(3x+26\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{26}{3}\end{matrix}\right.\\ d,\Leftrightarrow x^3-6x^2+12x-8-x^3-125-6x^2=11\\ \Leftrightarrow-12x^2+12x-144=0\\ \Leftrightarrow x^2-x+12=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=3\end{matrix}\right.\)

\(4x^2-3\left(2x-5\right)-25=0\Leftrightarrow4x^2-6x-10=0\)

\(\Leftrightarrow2\left(2x^2-3x-5\right)=0\Leftrightarrow2\left(x+1\right)\left(2x-5\right)=0\Leftrightarrow x=-1;x=\dfrac{5}{2}\)

4x²-3(2x-5)-25=0

⇒(2x)²-5²-3(2x-5)=0

⇒(2x-5)(2x+5)-3(2x-5)=0

⇒(2x-5)(2x+2)=0

⇒hoặc 2x-5=0⇒x=2,5

hoặc 2x+2=0⇒x=-1

vậy x={2,5;-1}