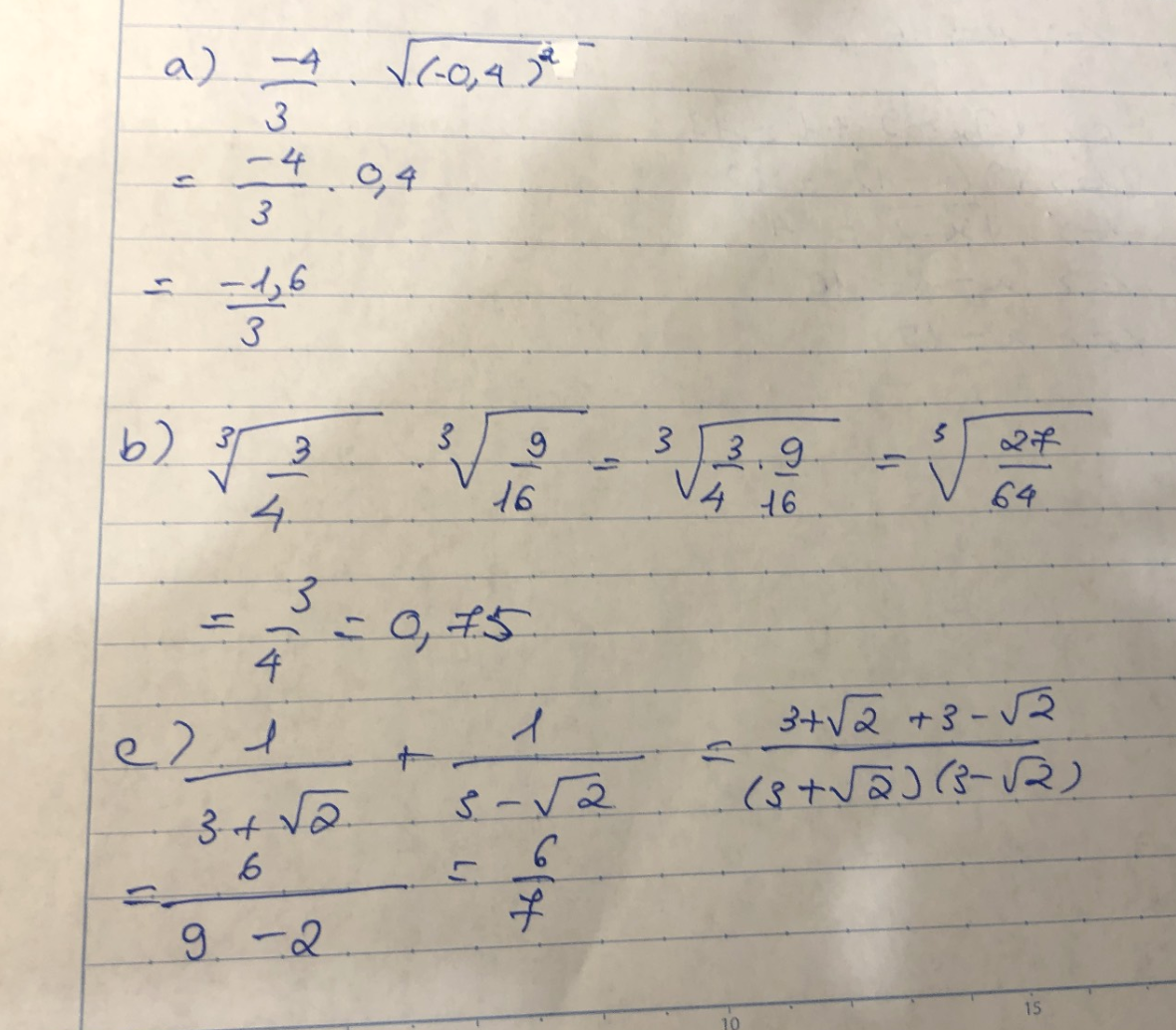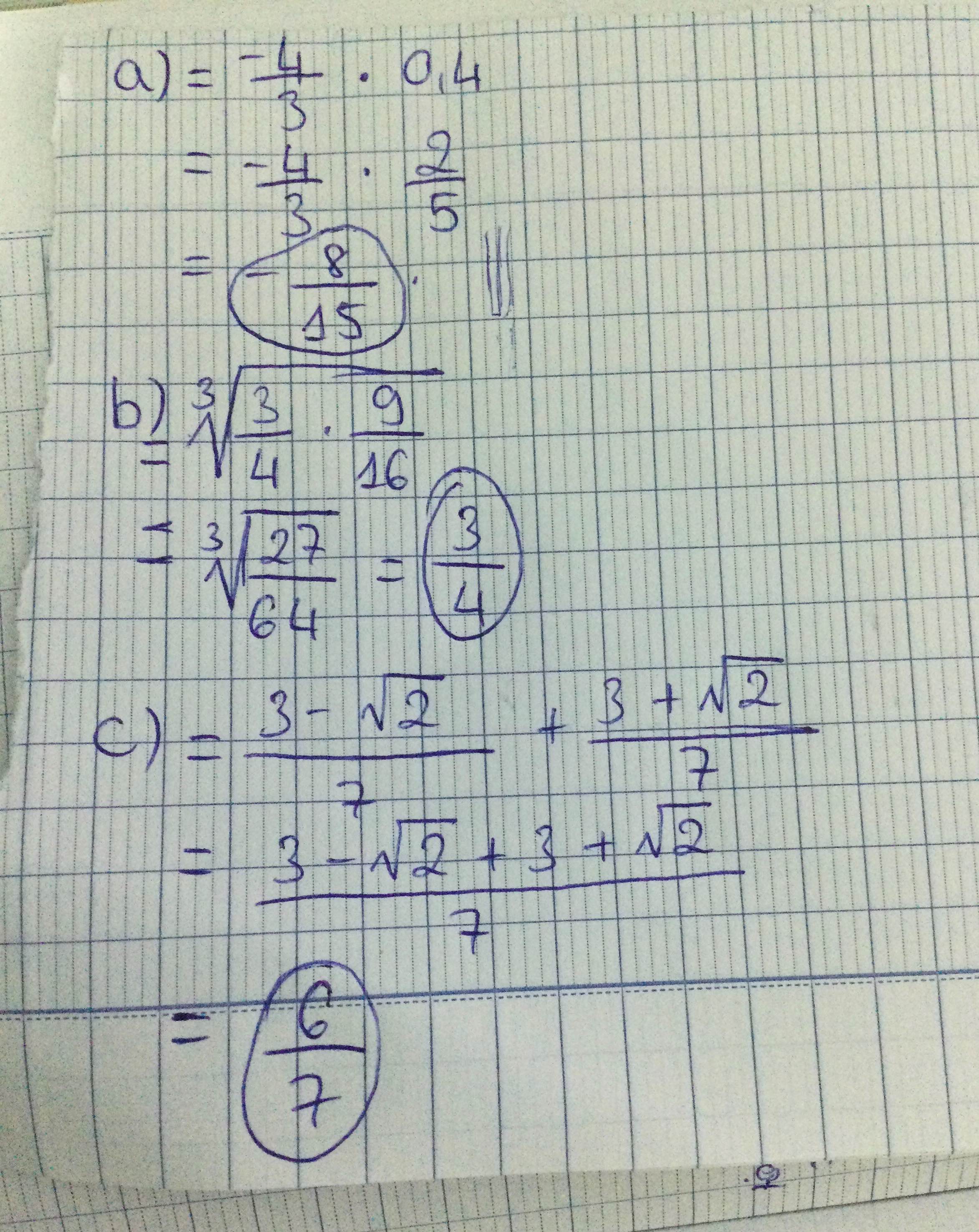\(a) \sqrt{4x^2− 9} = 2\sqrt{x + 3}\)

\(ĐK:x\ge\dfrac{3}{2}\)

\(pt\Leftrightarrow4x^2-9=4\left(x+3\right)\)

\(\Leftrightarrow4x^2-9=4x+12\)

\(\Leftrightarrow4x^2-4x-21=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{22}}{2}\left(l\right)\\x=\dfrac{1+\sqrt{22}}{2}\left(tm\right)\end{matrix}\right.\)

\(b)\sqrt{4x-20}+3.\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)

\(ĐK:x\ge5\)

\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)

\(\Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\)

\(\Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)

\(c)\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27.\sqrt{\dfrac{x-1}{81}}=4\)

ĐK:x>=1

\(pt\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\)

\(\Leftrightarrow4\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=1\)

\(\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)

\(d)5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)

\(ĐK:x\ge3\)

\(pt\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)

\(\Leftrightarrow-\dfrac{5}{3}\sqrt{x-3}-\sqrt{x^2-9}=0\Leftrightarrow\dfrac{5}{3}\sqrt{x-3}+\sqrt{x^2-9}=0\)

\(\Leftrightarrow(\dfrac{5}{3}+\sqrt{x+3})\sqrt{x-3}=0\)

\(\Leftrightarrow\sqrt{x-3}=0\)    (vì \(\dfrac{5}{3}+\sqrt{x+3}>0\))

\(\Leftrightarrow x-3=0\Leftrightarrow x=3\left(nhận\right)\)

 b) \(\sqrt{12-3\sqrt{7}}-\sqrt{12+3\sqrt{7}}\)

\(=\dfrac{\sqrt{2}\cdot\sqrt{12-3\sqrt{7}}-\sqrt{2}\cdot\sqrt{12+3\sqrt{7}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{24-6\sqrt{7}}-\sqrt{24+6\sqrt{7}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{\left(\sqrt{21}\right)^2-2\cdot\sqrt{21}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{21}\right)^2+2\cdot\sqrt{21}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{21}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{21}+\sqrt{3}\right)^2}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{21}-\sqrt{3}-\sqrt{21}-\sqrt{3}}{\sqrt{2}}\)

\(=\dfrac{-2\sqrt{3}}{\sqrt{2}}\)

\(=-\sqrt{6}\)  

c) \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}\)

\(=\sqrt[3]{\dfrac{3\cdot9}{4\cdot16}}\)

\(=\sqrt[3]{\left(\dfrac{3}{4}\right)^3}\)

\(=\dfrac{3}{4}\)

d) \(\dfrac{\sqrt[3]{54}}{\sqrt[3]{-2}}\)

\(=\sqrt[3]{\dfrac{54}{-2}}\)

\(=\sqrt[3]{-27}\)

\(=\sqrt[3]{\left(-3\right)^3}\)

\(=-3\) 

a: Sửa đề: \(\dfrac{1}{\sqrt{3}}+\dfrac{1}{3\sqrt{2}}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)

\(=\dfrac{1}{\sqrt{3}}+\dfrac{1}{\sqrt{3}\cdot\sqrt{6}}+\dfrac{\sqrt{3}-\sqrt{2}}{12}\)

\(=\dfrac{\sqrt{6}+1}{3\sqrt{2}}+\dfrac{\sqrt{3}-\sqrt{2}}{12}\)

\(=\dfrac{2\sqrt{2}\left(\sqrt{6}+1\right)+\sqrt{3}-\sqrt{2}}{12}\)

\(=\dfrac{4\sqrt{3}+2\sqrt{2}+\sqrt{3}-\sqrt{2}}{12}\)

\(=\dfrac{5\sqrt{3}+\sqrt{2}}{12}\)

e: \(\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}\)

\(=\sqrt[3]{2\sqrt{2}+3\sqrt{2}+6+1}-\sqrt[3]{2\sqrt{2}-3\sqrt{2}+6-1}\)

\(=\sqrt[3]{\left(\sqrt{2}+1\right)^3}-\sqrt[3]{\left(\sqrt{2}-1\right)^3}\)

\(=\sqrt{2}+1-\left(\sqrt{2}-1\right)\)

\(=\sqrt{2}+1-\sqrt{2}+1=2\)

a: Ta có: \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{x-4}\)

\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6+12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x+\sqrt{x}+22}{x-4}\)

d: Ta có: \(D=\dfrac{1}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}+\dfrac{2\sqrt{x}-12}{x-9}\)

\(=\dfrac{\sqrt{x}-3+x+3\sqrt{x}+2\sqrt{x}-12}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x+6\sqrt{x}-15}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

A=\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}A=\dfrac{\sqrt{x}+2.\left(\sqrt{x}+2\right)-3.\left(\sqrt{x}-2\right)+12}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}A=\dfrac{\sqrt{x}+2\sqrt{x}+4-3\sqrt{x}+6+12}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}A=\dfrac{22}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}\)

a) Ta có: \(\dfrac{-4}{3}\cdot\sqrt{\left(-0.4\right)^2}\)

\(=-\dfrac{4}{3}\cdot0.4\)

\(=\dfrac{-1.6}{3}=-\dfrac{8}{15}\)

b) Ta có: \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}\)

\(=\sqrt[3]{\dfrac{27}{64}}=\dfrac{3}{4}\)

c) Ta có: \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\)

\(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{7}\)

\(=\dfrac{6}{7}\)

a: \(\dfrac{-4}{3}\cdot\sqrt{\left(-0.4\right)^2}=\dfrac{-4}{3}\cdot\dfrac{2}{5}=\dfrac{-8}{15}\)

b: \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}=\dfrac{3}{4}\)

a: =(2căn 3-8căn 3)(căn 3-1)

=-6căn 3*(căn 3-1)

=-18+6căn 3

b: \(=\dfrac{6-2\sqrt{5}}{\sqrt{5}-3}-\sqrt{5}+2\)

=-2-căn 5+2=-căn 5

c: \(=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)

=\(3\sqrt{2a}-3a\cdot\sqrt{2a}\)

4 , Ta có :

\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x-9}{x-9}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-9}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{x-9}-\dfrac{3\left(x-3\right)}{x-9}\)

\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x+9}{x-9}\)

\(=\dfrac{3\sqrt{x}+9}{x-9}\)

\(=\dfrac{3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{3}{\sqrt{x}-3}\)

2 , Ta có :

\(\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)

\(=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x\sqrt{x}-x-\sqrt{x}+1}{x-1}\)

\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)

1: \(=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)-\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{15\sqrt{x}-11-3x-9\sqrt{x}+2\sqrt{x}+6-2x+2\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{-5\sqrt{x}+2}{\sqrt{x}+3}\)

3: \(=\dfrac{x-1-4\sqrt{x}+4+1}{x-1}\cdot\dfrac{x-1}{x-2\sqrt{x}}\)

\(=\dfrac{x-4\sqrt{x}+4}{x-2\sqrt{x}}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)

Đặt \(\sqrt[3]{2}=x\Rightarrow2=x^3\Rightarrow x^3+1=3;x^3-1=1\)

\(\sqrt[3]{\sqrt[3]{2}-1}=\sqrt[3]{x-1}=\sqrt[3]{\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x^2+x+1}}=\sqrt[3]{\dfrac{x^3-1}{x^2+x+1}}\)

\(=\sqrt[3]{\dfrac{1}{x^2+x+1}}=\sqrt[3]{\dfrac{1}{x^2+x+\dfrac{1}{3}\left(x^3+1\right)}}\)

\(=\sqrt[3]{\dfrac{3}{x^3+3x^2+3x+1}}=\sqrt[3]{\dfrac{27}{9\left(x+1\right)^3}}=\dfrac{1}{\sqrt[3]{9}}.\dfrac{3}{x+1}\)

\(=\dfrac{1}{\sqrt[3]{9}}\left(\dfrac{x^3+1}{x+1}\right)=\dfrac{1}{\sqrt[3]{9}}\left(1-x+x^2\right)=\dfrac{1}{\sqrt[3]{9}}\left(1-\sqrt[3]{2}+\sqrt[3]{4}\right)\)

\(=\sqrt[3]{\dfrac{1}{9}}-\sqrt[3]{\dfrac{2}{9}}+\sqrt[3]{\dfrac{4}{9}}\) (đpcm)