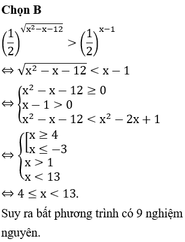\(=x-2x^2+2x^2-x+4\)

\(=4\)

\(x\left(1-2x\right)+\left(2x^2-x+4\right)\)

\(=x-2x^2+2x^2-x+4\)

\(=4\)>0

⇒ đa thức trên vô nghiệm

`x(1-2x)+(2x^2-x+4)=0`

`x-2x^2+2x^2-x+4=0`

`(x-x)+(2x^2-2x^2)+4=0`

`0x+4=0`

`=>` PTVN.

\(G\left(x\right)=x\left(1-2x\right)+\left(2x^2-x+4\right)\)

\(G\left(x\right)=x-2x^2+2x^2-x+4\)

\(G\left(x\right)=4\left(\ne0\right)\)

                           Vậy phương trình vô nghiệm

Bài 1:
1. 

$6x^3-2x^2=0$

$2x^2(3x-1)=0$

$\Rightarrow 2x^2=0$ hoặc $3x-1=0$

$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức

2.

$|3x+7|\geq 0$

$|2x^2-2|\geq 0$

Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$

$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý) 

Vậy đa thức vô nghiệm.

Bài 2:

1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$

Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$

Do đó đa thức vô nghiệm

2.

$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$

$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$

Vậy đa thức khác 0 với mọi $x$

Do đó đa thức không có nghiệm.

Bài 3:

$f(0)=a.0^3+b.0^2+c.0+d=d=5$

$f(1)=a+b+c+d=4$

$a+b+c=4-d=-1(*)$
$f(2)=8a+4b+2c+d=31$

$8a+4b+2c=31-d=26$

$4a+2b+c=13(**)$
$f(3)=27a+9b+3c+d=88$
$27a+9b+3c=88-d=83(***)$

Từ $(*); (**); (***)$ suy ra $a=\frac{1}{3}; b=13; c=\frac{-43}{3}$

Vậy.......

a) cho A(x) = 0

\(=>2x^2-4x=0\)

\(x\left(2-4x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)

b)\(B\left(y\right)=4y-8\)

cho B(y) = 0

\(4y-8=0\Rightarrow4y=8\Rightarrow y=2\)

c)\(C\left(t\right)=3t^2-6\)

cho C(t) = 0

\(=>3t^2-6=0=>3t^2=6=>t^2=2\left[{}\begin{matrix}t=\sqrt{2}\\t=-\sqrt{2}\end{matrix}\right.\)

d)\(M\left(x\right)=2x^2+1\)

cho M(x) = 0

\(2x^2+1=0\Rightarrow2x^2=-1\Rightarrow x^2=-\dfrac{1}{2}\left(vl\right)\)

vậy M(x) vô nghiệm

e) cho N(x) = 0

\(2x^2-8=0\)

\(2\left(x^2-4\right)=0\)

\(2\left(x^2+2x-2x-4\right)=0\)

\(2\left(x-2\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

`e, N(x) = 2x^2 - 8 = 2( x^2 - 4 ) = 2( x-2 )( x + 2 )`

Xét `N(x)=0`

`=> 2(x-2)(x+2)=0`

`=>(x-2)(x+2)=0`

`=>x-2=0` hoặc `x+2=0`

`=>x=2` hoặc `x=-2`

Vậy `x in { +-2 }` là nghiệm của `N(x)` 

Bài 1 : 

Để phương trình có 2 nghiệm x₁ , x₂ 

\(\Rightarrow\Delta'=\left(-1\right)^2-\left(2m-1\right)\ge0\)

\(\Rightarrow m\le1\)

\(\Rightarrow\) Khi đó phương trình có 2 nghiệm x₁ , x₂ thỏa mãn 

\(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=2m-1\end{cases}}\)

Mà \(3x_1+2x_2=1\Rightarrow x_1+2\left(x_1+x_2\right)=1\Rightarrow x_1+2.2=1\Rightarrow x_1=-3\)

Vì \(x_1=-3\) là 1 nghiệm của phương trình

\(\Rightarrow\left(-3\right)^2-2\left(-3\right)+2m-1=0\Rightarrow m=-7\)

Bài 2 : 

\(ĐKXĐ:x\ne\pm4\)

Ta có : 

\(\frac{2x-1}{x+4}-\frac{3x-1}{4-x}=5+\frac{96}{x^2-16}\)

\(\Rightarrow\frac{2x-1}{x+4}+\frac{3x-1}{x-4}=5+\frac{96}{\left(x-4\right)\left(x+4\right)}\)

\(\Rightarrow\frac{2x-1}{x+4}\left(x+4\right)\left(x-4\right)+\frac{96}{\left(x-4\right)\left(x+4\right)}\left(x+4\right)\left(x-4\right)\)

\(\Rightarrow\left(2x-1\right)\left(x-4\right)+\left(3x-1\right)\left(x+4\right)=5\left(x+4\right)\left(x-4\right)+96\)

\(\Rightarrow5x^2+2x=5x^2+16\)

\(\Rightarrow2x=16\)

\(\Rightarrow x=8\)

a: \(A=-5x^3+9x^3-2x^2-2x^2+x-x+1\)

\(=4x^3-4x^2+1\)

\(B=-4x^3+2x^3-2x^2+2x^2+6x-9x-2\)

\(=-2x^3-3x-2\)

\(C=x^3-6x^2+2x-4\)

b: \(A\left(x\right)+B\left(x\right)-C\left(x\right)\)

\(=4x^3-4x^2+1-2x^3-3x-2+x^3-6x^2+2x-4\)

\(=3x^3-10x^2-x-4\)

a) Ta có: \(x^2\left(x+1\right)+x+1=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow x+1=0\)

hay x=-1

b) Ta có: \(x^2-x=-2x^2+2x\)

\(\Leftrightarrow3x^2-3x=0\)

\(\Leftrightarrow3x\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

c) Ta có: \(2x^2\left(x-1\right)+x^2=x\)

\(\Leftrightarrow2x^2\left(x-1\right)+x^2-x=0\)

\(\Leftrightarrow2x^2\left(x-1\right)+x\left(x-1\right)=0\)

\(\Leftrightarrow x\left(x-1\right)\cdot\left(2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{-1}{2}\end{matrix}\right.\)

d) Ta có: \(\left(x-2\right)\left(x^2+4\right)=x^2-2x\)

\(\Leftrightarrow\left(x-2\right)\left(x^2+4\right)-x\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-x+4\right)=0\)

\(\Leftrightarrow x-2=0\)

hay x=2