ĐKXĐ: \(x\ne2;x\ne\dfrac{3}{2}\)

ĐKXĐ: \(x\ge0\)

ĐKXĐcủa√x+3=x≥0

Để \(\sqrt{x}-1\) được xác định cần:

\(\sqrt{x}\ge0\)

<=> \(x\ge0\)

Vậy ĐKXĐ của \(\sqrt{x}-1\) là \(x\ge0\)

Căn thức có nghiệm khi giá trị trong căn lớn hơn hoặc bằng 0 còn phép cộng đúng với mọi x nên x \(\ne1\) là sai nhé

\(a,P=\dfrac{81-9}{9-3}=\dfrac{72}{6}=12\\ b,Q=\dfrac{3\sqrt{a}+9+2\sqrt{a}-6+a-5\sqrt{a}-3}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}\\ Q=\dfrac{a}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}\\ c,A=PQ=\dfrac{a\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}{\left(\sqrt{a}-3\right)^2\left(\sqrt{a}+3\right)}=\dfrac{a}{\sqrt{a}-3}\\ A=\dfrac{a-9+9}{\sqrt{a}-3}=\sqrt{a}+3+\dfrac{9}{\sqrt{a}-3}\\ A=\sqrt{a}-3+\dfrac{9}{\sqrt{a}-3}+6\ge2\cdot3+6=12\\ A_{min}=12\Leftrightarrow\left(\sqrt{a}-3\right)^2=9\Leftrightarrow\left[{}\begin{matrix}\sqrt{a}-3=3\\\sqrt{a}-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=36\left(tm\right)\\a=0\left(tm\right)\end{matrix}\right.\)

\(a,ĐK:x\le2\\ PT\Leftrightarrow x^2-x-8=4-2x\Leftrightarrow x^2+x-12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\Leftrightarrow x=-4\\ b,ĐK:5x^2+10x+1\ge0\\ PT\Leftrightarrow5x^2+10x+1=\left(7-x^2-2x\right)^2\\ \Leftrightarrow5x^2+10x+1=x^4+4x^2+49-14x^2+4x^3-28x\\ \Leftrightarrow x^4+4x^3-15x^2-38x+48=0\\ \Leftrightarrow x^4-x^3+5x^3-5x^2-10x^2+10x-48x+48=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+5x^2-10x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+3x^2+2x^2+6x-16x-48\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)\left(x^2+2x-16\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\\x^2+2x-16=0\left(1\right)\end{matrix}\right.\)

\(\Delta\left(1\right)=4+64=68\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-2\sqrt{17}}{2}=-1-\sqrt{17}\\x=\dfrac{-2+2\sqrt{17}}{2}=-1+\sqrt{17}\end{matrix}\right.\)

Vậy pt có nghiệm ...

ĐKXĐ : \(2x-x^2-3\ne0\Rightarrow-x^2+2x-3\ne0\)

\(\Rightarrow-\left(x^2-2x+3\right)\ne0\Rightarrow x^2-2.x+1+2\ne0\)

\(\Rightarrow\left(x-1\right)^2+2\ne0\)

VÌ \(\left(x-1\right)^2\ge0\) dấu = khi x=1 

                \(2>0\)

\(\Rightarrow\left(x-1\right)^2+2>0\)

\(\Rightarrow\left(x-1\right)^2+2\ne0\) luôn đúng 

\(\Rightarrow2x-x^2-3\ne0\) luôn đúng 

\(\Rightarrow\text{Đ}K\text{X}\text{Đ}:x\in R\)

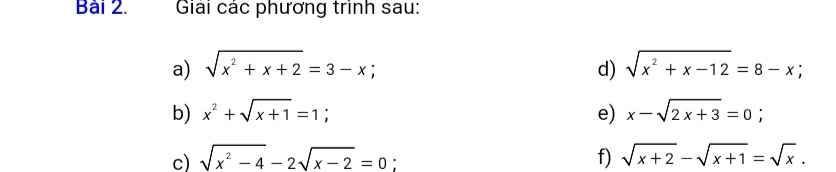
a. ĐKXĐ: $x\in\mathbb{R}$

PT \(\Rightarrow \left\{\begin{matrix} 2-x\geq 0\\ x^2+x+2=(3-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ x^2+x+2=x^2-6x+9\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 7x=7\end{matrix}\right.\Leftrightarrow x=1\)

b. ĐKXĐ: $x\geq -1$

PT $\Leftrightarrow (x^2-1)+\sqrt{x+1}=0$

$\Leftrightarrow (x-1)(x+1)+\sqrt{x+1}=0$

$\Leftrightarrow \sqrt{x+1}[(x-1)\sqrt{x+1}+1]=0$

$\Leftrightarrow \sqrt{x+1}=0$ hoặc $(x-1)\sqrt{x+1}+1=0$

Nếu $\sqrt{x+1}=0$

$\Leftrightarrow x=-1$ (tm)

Nếu $(x-1)\sqrt{x+1}+1=0$

$\Leftrightarrow (x-1)\sqrt{x+1}=-1$

$\Rightarrow (x-1)^2(x+1)=1$

$\Leftrightarrow x^3-x^2-x=0$

$\Leftrightarrow x(x^2-x-1)=0$

$\Leftrightarrow x=0$ hoặc $x^2-x-1=0$

$\Leftrightarrow x=0$ hoặc $x=\frac{1\pm \sqrt{5}}{2}$

Kết hợp đkxđ suy ra $x=0; -1; \frac{1\pm \sqrt{5}}{2}$

c. ĐKXĐ: $x\geq 2$

PT $\Leftrightarrow \sqrt{(x-2)(x+2)}-2\sqrt{x-2}=0$

$\Leftrightarrow \sqrt{x-2}(\sqrt{x+2}-2)=0$

$\Leftrightarrow \sqrt{x-2}=0$ hoặc $\sqrt{x+2}-2=0$

$\Leftrightarrow x=2$  (thỏa mãn)

d. ĐKXĐ: $x\geq 3$ hoặc $x\leq -4$

PT \(\Rightarrow \left\{\begin{matrix} 8-x\geq 0\\ x^2+x-12=(8-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ x^2+x-12=x^2-16x+64\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ 17x=76\end{matrix}\right.\Leftrightarrow x=\frac{76}{17}\) (tm)

e. ĐKXĐ: $x\geq \frac{-3}{2}$
PT $\Leftrightarrow x=\sqrt{2x+3}$

\(\Rightarrow \left\{\begin{matrix} x\geq 0\\ x^2=2x+3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ (x-3)(x+1)=0\end{matrix}\right.\Leftrightarrow x=3\) (tm)

f. ĐKXĐ: $x\geq 0$

PT $\Leftrightarrow \sqrt{x+2}=\sqrt{x}+\sqrt{x+1}$

$\Leftrightarrow x+2=2x+1+2\sqrt{x(x+1)}$ (bp hai vế)

$\Leftrightarrow 1-x=2\sqrt{x(x+1)}$

\(\Rightarrow \left\{\begin{matrix} 1-x\geq 0\\ (1-x)^2=4x(x+1)\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 1\\ 3x^2+6x-1=0\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\leq 1\\ x=\frac{-3\pm 2\sqrt{3}}{3}\end{matrix}\right.\)

Kết hợp cả đkxđ suy ra  $x=\frac{-3+2\sqrt{3}}{3}$

vì x > 2 mà lại nhỏ hơn hoặc =4 nên x có 2 nghiệm là 3; 4 thỏa mãn

cũng như bn có số quả táo nhiều hơn 2 mà ít hơn 5 thì bn có 3 hoặc 4 quả

3-2x <= 15-5x

5x-2x <= 15-3

x<= 4

3-2x <7

x>2

kết hợp nghiệm ta có;

2<x<=4

vậy x = 3; 4 thỏa mãn 

tại sao lại thảo mãn vs 3 nữa vậy bạn? :)) hỏi ngu