cho tam giác ABC vuông tại A trên cạnh BC lấy điểm E sao cho BE=BA.từ Eker dường thẳng vuông góc với BC,dường thẳng này cắt AC tại D
a,CMR:tam giác ABD=tam giác EBD
b,đường thẳng DE cắt đường thẳng AB tại I.CMR tam giác BCI cân
c,gọi M là trung điểm của CI.CMR:B,D,M thẳng hàng
d,gọi K là giao điểm của AE và BD.CMR:AK+BD >AB+AD

Những câu hỏi liên quan
Tam giác ABC vuông tại A biết góc ABC= 60 độ và AB= 6 cm. Trên cạnh BC lấy điểm E sao cho BA=BE. Đường thẳng vuông góc với BC tại E cắt AC tại D
a) CM: tam giác ABD= tam giác EBD
b) CM: tam giác ABE đều, tính BC
c) Vẽ AH vuông góc với BC (H thuộc BC). Tia phân giác của góc BAH cắt BC tại G
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
b: Xét ΔBAE có BA=BE và góc B=60 độ
nên ΔBAE đều
=>BE=AB=6cm
=>BC=12cm
Đúng 0
Bình luận (0)
CHo tam giác ABC có AB=9cm, AC= 12 cm và BC = 15 cm. Vẽ tia phân giác của góc B cắt cạnh AC tại D. Trên cạnh BC lấy điểm E sao cho BE=BA. Đường thẳng DE cắt đường thẳng AB tại F. a, Chứng minh tam giác ABC vuông. b, Chứng minh DE vuông góc với BC rồi so sánh AD và DC. c, Gọi M, N lần lượt là trung điểm của AE và CF. CHứng minh ba điểm M,D,N thẳng hàng
mn giúp mik vs mik cần gấp.
Cho tam giác ABC vuông tại A, phân giác của góc ABC cắt cạnh AC tại D. Trên cạnh BC lấy E sao cho BE=BA. Đường thẳng DE cắt đường thẳng AB tại F. Chứng minh
a. Tam giác ABD=EBD
b. DE vuông góc BC.
c. AF=EC
GIÚP MK NHA
Xét \(\Delta ABD\) và \(\Delta EBD\)
ta có DA = DE ( gt )
BA = BE ( gt )
BD là cạnh chung
=> \(\Delta ABD=\Delta EBD\left(c.c.c\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, có AB36cm, BC39cma/ Tính độ dài cạnh AC và so sánh các góc tam giác ABCb/ Trên tia đối tia AC lấy điểm D sao cho A là trung điểm của đoạn thẳng ACC/M: t/giác ABC t/giác ABDc/ Trên tia AC lấy điểm E sao cho C là trung điểm của đoạn AE. Gọi F là trung điểm đoạn AB. Đường EF cắt cạnh BC tại G. Tính độ dài đoạn thẳng BGd/ Từ C vẽ đường thẳng vuông góc voiwscanhj BD tại M, đường thẳng này cắt cạnh AB tại H, Qua C vẽ đường thẳng vuông góc với cạnh BC, đường thẳng này cắt...
Đọc tiếp
cho tam giác ABC vuông tại A, có AB=36cm, BC=39cm
a/ Tính độ dài cạnh AC và so sánh các góc tam giác ABC
b/ Trên tia đối tia AC lấy điểm D sao cho A là trung điểm của đoạn thẳng AC
C/M: t/giác ABC = t/giác ABD
c/ Trên tia AC lấy điểm E sao cho C là trung điểm của đoạn AE. Gọi F là trung điểm đoạn AB. Đường EF cắt cạnh BC tại G. Tính độ dài đoạn thẳng BG
d/ Từ C vẽ đường thẳng vuông góc voiwscanhj BD tại M, đường thẳng này cắt cạnh AB tại H, Qua C vẽ đường thẳng vuông góc với cạnh BC, đường thẳng này cắt cạnh BA tại K.
C/M: t/giác CHK cân
Cho ABC vuông tại A có AB AC, Trên cạnh BC lấy điểm D sao cho BA BD. Từ D kẻ DE BC (E AC), Đường thẳng DE cắt đường thẳng AB tại M. Chứng minh rằng a) Tam giác ABE Tam giác DBE b) BE Vuông Góc AD c) Tam giác MBC cân
Đọc tiếp
Cho ABC vuông tại A có AB < AC, Trên cạnh BC lấy điểm D sao cho BA = BD. Từ D kẻ DE BC (E AC), Đường thẳng DE cắt đường thẳng AB tại M. Chứng minh rằng
a) Tam giác ABE = Tam giác DBE
b) BE Vuông Góc AD
c) Tam giác MBC cân
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D co
BE chung
BA=BD
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc B chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
Đúng 1
Bình luận (1)
`a,`
Xét `2 \Delta` vuông `ABE` và `DBE`:
`\text {BE chung}`
`\text {BA = BD (2 cạnh tương ứng)}`
`=> \Delta ABE = \Delta DBE (ch-cgv)`
`b,`
Gọi I là giao điểm của AD và BE
Vì `\Delta ABE = \Delta DBE (a)`
`->` $\widehat {ABE} = \widehat {DBE} (\text {2 góc tương ứng})$
Xét `\Delta ABI` và `\Delta DBI`:
`\text {BA = BD (gt)}`
$\widehat {ABI} = \widehat {DBI}$
`\text {BI chung}`
`=> \Delta ABI = \Delta DBI (c-g-c)`
`->` $\widehat {BIA} = \widehat {BID} (\text {2 cạnh tương ứng})$
Mà `2` góc này ở vị trí kề bù
`->` $\widehat {BIA} + \widehat {BID} = 180^0$
`->` $\widehat {BIA} = \widehat {BID} =$\(\dfrac{180}{2}=90^0\)
`-> \text {BI} \bot \text {AD}`
Mà `\text {I} \in \text {BE}`
`-> \text {BE} \bot \text{AD}`
`c,`
Vì `\Delta ABE = \Delta DBE (a)`
`-> \text {AE = DE (2 cạnh tương ứng)}`
Xét `\Delta AEM` và `\Delta DEC`:
`\text {AE = DE}`
$\widehat {AEM} = \widehat {DEC} (\text {2 góc đối đỉnh})$
$\widehat {MAE} = \widehat {CDE} (=90^0)$
`=> \Delta AEM = \Delta DEC (cgv-gn)`
`-> \text {AM = DC (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{BM = AM + AB}\\\text{BC = BD + DC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{BA = BD}\\\text{AM = DC}\end{matrix}\right.\)
`-> \text {BM = BC}`
Xét `\Delta MBC`:
`\text {BM = BC}`
`-> \Delta MBC` cân tại B.
Đúng 0
Bình luận (0)
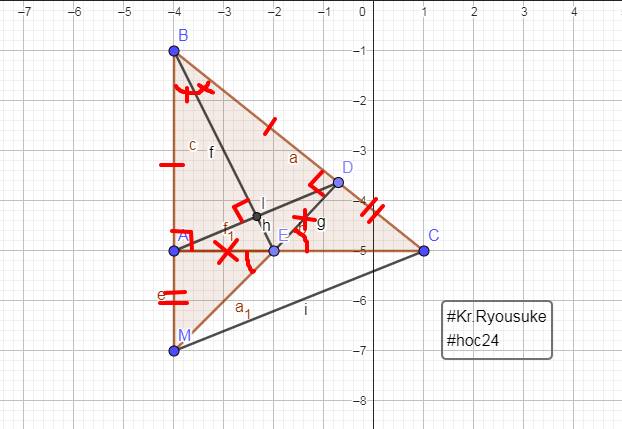
Cho tam giác abc vuông tạ a( ab<ac) kẻ bd là tia phân giác của góc abc (d thuộc ac), trên cạnh BC lấy điểm E sao cho AB=AE
a) Chứng minh tam giác ABD=tam giác EBD
b) So sánh AD và DC
c) Đường thẳng ED cắt đường thẳng AB tại F, gọi S là trung điểm của FC. Chứng minh ba điểm B, D, S thẳng hàng
a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
Đúng 0
Bình luận (0)
Sửa đề: AB = BE (không phải AB = AE)
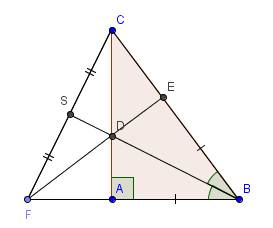
Gởi hình vẽ trước, đi công việc, tí sửa sau
Đúng 1
Bình luận (0)
Xét ∆ABD và ∆EBD có:
∠ABD = ∠EBD (do BD là phân giác của ∠B)
BD chung
AB = BE (gt)
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ ∠CED = 90⁰
⇒ ∆CED vuông tại E
⇒ CD là cạnh huyền nên là cạnh lớn nhất
⇒ CD > DE (1)
Do ∆ABD = ∆EBD (cmt)
⇒ AD = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ CD > AD
c) Xét hai tam giác vuông:
∆ABC và ∆EBF có:
AB = BE (gt)
∠B chung
⇒ ∆ABC = ∆EBF (cạnh góc vuông - góc nhọn kề)
⇒ BC = BF (hai cạnh tương ứng)
⇒ ∆BCF cân tại B
Lại có BD là phân giác của ∠B
⇒ BD cũng là đường trung tuyến của ∆BCF
Mà S là trung điểm FC
⇒ B, D, S thẳng hàng
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A và có AB < AC. Tia phân giác của góc ABC cắt AC tại E. Từ A kẻ đường thẳng vuông góc với BE tại H , đường thẳng này cắt BC tại D
a)Chứng minh BA = BD
b)Chứng minh BD vuông góc với BC
c) Trên tia đối tia AB lấy điểm F sao cho AF = DC. Chứng minh ba điểm F , E , D
Cho Tam giác ABC vuông tại A . Vẽ tia phân giác góc B cắt AC tại D ( D thuộc AC) . Kẻ ĐỂ vuông góc với BC tại E
a) Chứng minh: tam giác ABD = tam giác EBD
b) Chứng minh BD là đường trung trực của đoạn thẳng AE.
c) Đường thẳng AB cắt đường thẳng DE tại F . Chứng minh AE // CF
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD la trung trực của AE
c: Xét ΔBEF vuông tại E và ΔBAC vuông tại A co
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
Xét ΔFCB có BA/BF=BE/BC
nên AE//CF
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho CE BD. Đường thẳng vuông góc với BC kẻ từ D cắt AB tại M. Đường vuông góc với BE tại E cắt AC tại N.a. CMR: tam giác MBD tam giác NCE.b. Cạnh BC cắt MN tại I. CMR: MI IN.c. Chứng minh đường thẳng vuông góc với MN tại I luôn đi qua 1 điểm cố định khi D thay đổi trên đoạn BC.Mk giải được câu a, b rùi. Các bn giúp mk câu c vs!!!
Đọc tiếp
Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho CE = BD. Đường thẳng vuông góc với BC kẻ từ D cắt AB tại M. Đường vuông góc với BE tại E cắt AC tại N.
a. CMR: tam giác MBD = tam giác NCE.
b. Cạnh BC cắt MN tại I. CMR: MI = IN.
c. Chứng minh đường thẳng vuông góc với MN tại I luôn đi qua 1 điểm cố định khi D thay đổi trên đoạn BC.
Mk giải được câu a, b rùi. Các bn giúp mk câu c vs!!!
-Câu 1,2 của bài này na ná với nhau á, bạn tham khảo:
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-can-tai-a-tren-canh-bc-lay-d-d-khong-trung-b-va-bdbc2-tren-tia-doi-cua-tia-cb-lay-e-sao-cho-bdce-cac-duong-vuong-goc-voi-bc-ke-tu-d-va-e-cat-duong-thang-ab-va-ac-lan-luot-tai.4784314158042
Đúng 1
Bình luận (0)
c. -Kẻ tia phân giác của \(\widehat{BAC}\) cắt đường vuông góc với MN (tại I) tại F.
-Xét △ABF và △ACF:
\(AB=AC\) (△ABC cân tại A).
\(\widehat{BAF}=\widehat{CAF}\) (AF là tia phân giác của \(\widehat{BAC}\))
AF là cạnh chung.
\(\Rightarrow\)△ABF=△ACF (c-g-c).
\(\Rightarrow BF=CF\) (2 cạnh tương ứng).
\(\widehat{ABF}=\widehat{ACF}\) (2 góc tương ứng).
-Xét △MIF và △NIF:
\(MI=IN\left(cmt\right)\)
\(\widehat{MIF}=\widehat{NIF}=90^0\)
IF là cạnh chung.
\(\Rightarrow\)△MIF=△NIF (c-g-c).
\(\Rightarrow MF=NF\) (2 cạnh tương ứng).
-Xét △BMF và △CNF:
\(BM=NC\)(△MBD=△NCE)
\(MF=NF\left(cmt\right)\)
\(BF=CF\left(cmt\right)\)
\(\Rightarrow\)△BMF=△CNF (c-c-c).
\(\Rightarrow\widehat{MBF}=\widehat{NCF}\) (2 cạnh tương ứng).
Mà \(\widehat{MBF}=\widehat{MCF}\)(cmt)
\(\Rightarrow\widehat{NCF}=\widehat{MCF}\)
Mà \(\widehat{NCF}+\widehat{MCF}=180^0\) (kề bù)
\(\Rightarrow\widehat{NCF}=\widehat{MCF}=\dfrac{180^0}{2}=90^0\)
\(\Rightarrow\)AB⊥BF tại B.
\(\Rightarrow\) F là giao của đường vuông góc với AB tại B và tia phân giác của góc \(\widehat{BAC}\).
\(\Rightarrow\)F cố định.
-Vậy đường thẳng vuông góc với MN luôn đi qua điểm cố định khi D thay đổi trên đoạn BC.
Đúng 1
Bình luận (0)

























