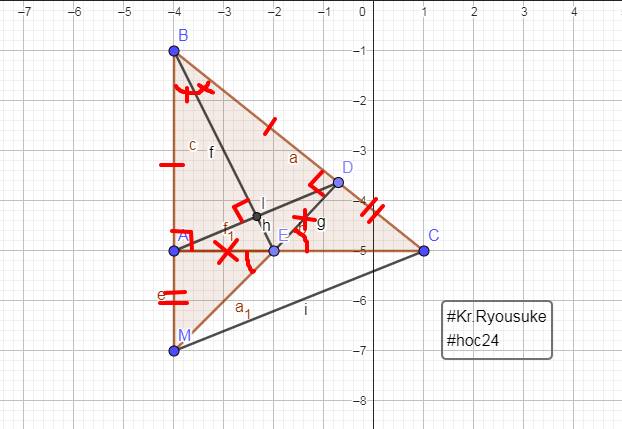
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D co
BE chung
BA=BD
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc B chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
`a,`
Xét `2 \Delta` vuông `ABE` và `DBE`:
`\text {BE chung}`
`\text {BA = BD (2 cạnh tương ứng)}`
`=> \Delta ABE = \Delta DBE (ch-cgv)`
`b,`
Gọi I là giao điểm của AD và BE
Vì `\Delta ABE = \Delta DBE (a)`
`->` $\widehat {ABE} = \widehat {DBE} (\text {2 góc tương ứng})$
Xét `\Delta ABI` và `\Delta DBI`:
`\text {BA = BD (gt)}`
$\widehat {ABI} = \widehat {DBI}$
`\text {BI chung}`
`=> \Delta ABI = \Delta DBI (c-g-c)`
`->` $\widehat {BIA} = \widehat {BID} (\text {2 cạnh tương ứng})$
Mà `2` góc này ở vị trí kề bù
`->` $\widehat {BIA} + \widehat {BID} = 180^0$
`->` $\widehat {BIA} = \widehat {BID} =$\(\dfrac{180}{2}=90^0\)
`-> \text {BI} \bot \text {AD}`
Mà `\text {I} \in \text {BE}`
`-> \text {BE} \bot \text{AD}`
`c,`
Vì `\Delta ABE = \Delta DBE (a)`
`-> \text {AE = DE (2 cạnh tương ứng)}`
Xét `\Delta AEM` và `\Delta DEC`:
`\text {AE = DE}`
$\widehat {AEM} = \widehat {DEC} (\text {2 góc đối đỉnh})$
$\widehat {MAE} = \widehat {CDE} (=90^0)$
`=> \Delta AEM = \Delta DEC (cgv-gn)`
`-> \text {AM = DC (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{BM = AM + AB}\\\text{BC = BD + DC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{BA = BD}\\\text{AM = DC}\end{matrix}\right.\)
`-> \text {BM = BC}`
Xét `\Delta MBC`:
`\text {BM = BC}`
`-> \Delta MBC` cân tại B.