Giúp e câu 9 10 đi ạ scan vẽ hình thì vẽ luôn ạ

Những câu hỏi liên quan
Giúp e câu 11 vẽ hình luôn ạ
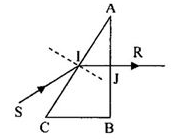
Theo đinh luật khúc xạ ánh sáng (tại điểm \(I\)) :
\(sini_1=nsinr_1\)
\(\Rightarrow sin45^o=\sqrt{2}\cdot sinr_1\Rightarrow sinr_1=\dfrac{1}{2}\Rightarrow r_1=30^o\)
Tam giác ABC đều\(\Rightarrow\)Góc chiết quang \(\widehat{A}=60^o=r_1+r_2\)
\(\Rightarrow r_2=30^o\)
Xét tại điểm J, theo định luật khúc xạ ánh sáng:
\(sini_2=nsinr_2=\sqrt{2}\cdot sin30^o=\dfrac{\sqrt{2}}{2}\Rightarrow i_2=45^o\)
Góc lệch tia ló ra khỏi lăng kính so với tia tới:
\(D=i_1+i_2-A=45^o+45^o-60^o=30^o\)
Chọn A
Đúng 1
Bình luận (0)
Giúp e vẽ hình và giải chi tiết câu 9 đi ạ
Góc giới hạn phản xạ toàn phần:
\(sini_{gh}=\dfrac{n_2}{n_1}\)
\(\Rightarrow sini_{gh}=\dfrac{\dfrac{4}{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}}{9}\)
\(\Rightarrow i_{gh}=50,2^o\)
Chọn A
Đúng 2
Bình luận (0)
dạ giúp e câu 2 phần c (c/m DK // BC) e cho kẹo ạ :3
e vẽ hình luôn ròi nha
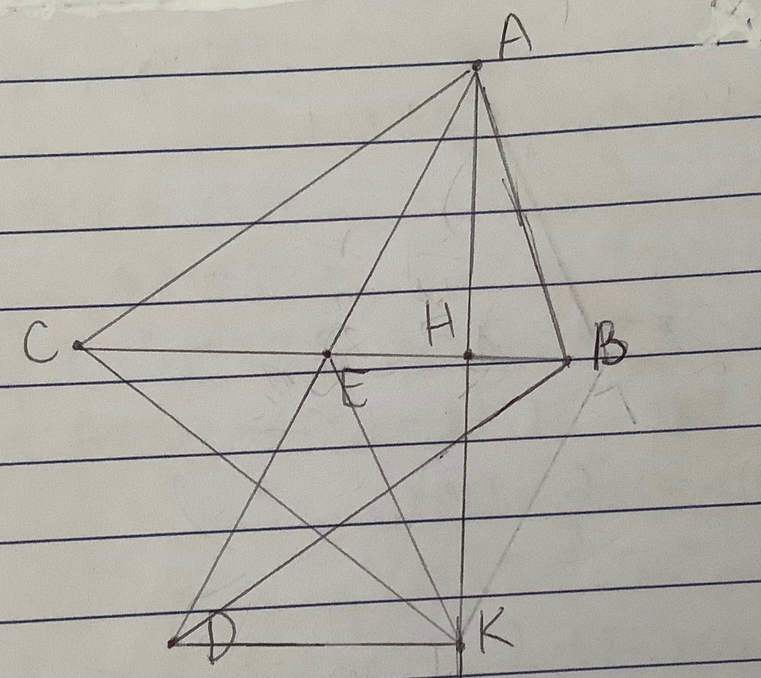


Ta có:\(AH=HK\left(gt\right);AE=ED\left(gt\right)\Rightarrow\)EH là đường trung bình trong tam giác AKD⇒EH//DK⇒BC//DK
Đúng 1
Bình luận (5)
Nối BK và CP
Xét ΔBEK và ΔCED có:
\(BE=CE\left(gt\right)\)
\(\widehat{BEK}=\widehat{CED}\left(=\widehat{BEA}\right)\)
\(EK=ED\left(=AE\right)\)
⇒ΔBEK = ΔCED (c.g.c)
⇒KE=DE (2 cạnh tương ứng)
⇒ΔDEK cân tại E⇒\(\widehat{EKD}=\widehat{EDK}\)
ΔBEK = ΔCED (cmt)⇒\(\widehat{BEK}=\widehat{CED}\)
Ta có: \(\widehat{BEK}+\widehat{KED}+\widehat{CED}=180^o\Rightarrow2\widehat{BEK}=180^o-\widehat{KED}\)(1)
Xét ΔKED có:\(\widehat{KED}+\widehat{EKD}+\widehat{EDK}=180^o\Rightarrow2\widehat{EKD}=180^o-\widehat{KED}\)(2)
Từ (1) và (2)⇒\(2\widehat{BEK}=2\widehat{EKD}\Rightarrow\widehat{BEK}=\widehat{EKD}\)
Mà 2 góc này là 2 góc so le trong ⇒BE//KD⇒BC//KD
Đúng 0
Bình luận (0)
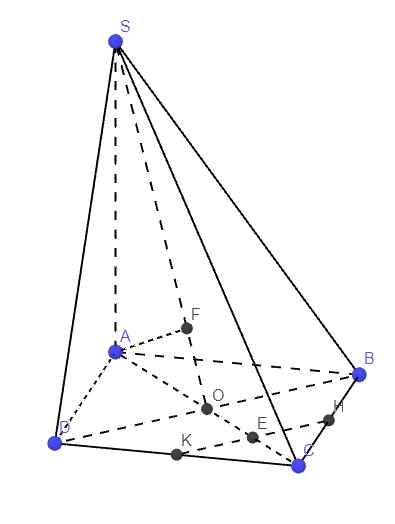
Giúp e vẽ hình và làm câu 34 đi ạ 

Gọi E là giao điểm HK và AC
\(\Rightarrow E\) là trung điểm OC \(\Rightarrow OE=\dfrac{1}{2}OC=\dfrac{1}{2}OA\)
\(\Rightarrow d\left(E;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
HK là đường trung bình tam giác BCD \(\Rightarrow HK||BD\)
\(\Rightarrow d\left(HK;SD\right)=d\left(HK;\left(SBD\right)\right)=d\left(E;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
Từ A kẻ \(AF\perp SO\Rightarrow AF\perp\left(SBD\right)\Rightarrow AF=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng:
\(AF=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2a}{3}\)
\(\Rightarrow d\left(HK;SD\right)=\dfrac{1}{2}AF=\dfrac{a}{3}\)
Đúng 0
Bình luận (0)
Bài 6: Cho hình vẽ: Biết . HEF = 120 Ta có, (vẽ hình giúp e ạ và vẽ hình câu c đi ạ)c) Vẽ Hm và En lần lượt là tia phân giác của GHE và HEF. Chứng minh Nm // En
Xem chi tiết
Giúp e câu 12 vẽ hình giải chi tiết đi ạ
Câu 12.
Ta có: \(\dfrac{sini}{sinr}=n\Rightarrow\dfrac{sin60^o}{sinr}=1,5\)
\(\Rightarrow sinr=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow r\approx35,3^o\)
Chọn C
Đúng 2
Bình luận (0)
Giúp e bài 4 vs ạ(có vẽ hình),e cần cách lm dễ hiểu chi tiết,bài này e cần lắm luôn đó ạ nên giúp e lm đúng vs(nếu mn có thời gian thì giúp e luôn bài 2 vs,e ko đc chắc chắn bài này e lm có đúng ko)e cảm ơn nhìu lắm ạ!!!
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Đúng 1
Bình luận (0)
Giúp e giải và vẽ hình câu 17 chi tiết đi ạ
Câu 17.
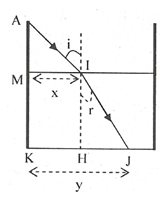
Xét tam giác IHJ vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
Chiết xuất: \(\dfrac{sini}{sinr}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{3}{4}\cdot\dfrac{60^2+HJ^2}{HJ^2}=\dfrac{16}{9}\Rightarrow HJ=51,25cm\)
Độ dài bóng của thành bể tạo ở đáy:
\(HJ+x=85,9cm\)
Chọn A
Đúng 2
Bình luận (0)
Giúp e vẽ hình và giải chi tiết câu 14 đi ạ
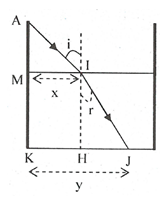
Xét \(\Delta HIJ\) vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
\(\Rightarrow\dfrac{sini}{sinr}=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{60^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow HJ=51,25cm\)
Độ dài vệt sáng:
\(y=x+HJ=85,9cm\)
Chọn B
Đúng 2
Bình luận (0)