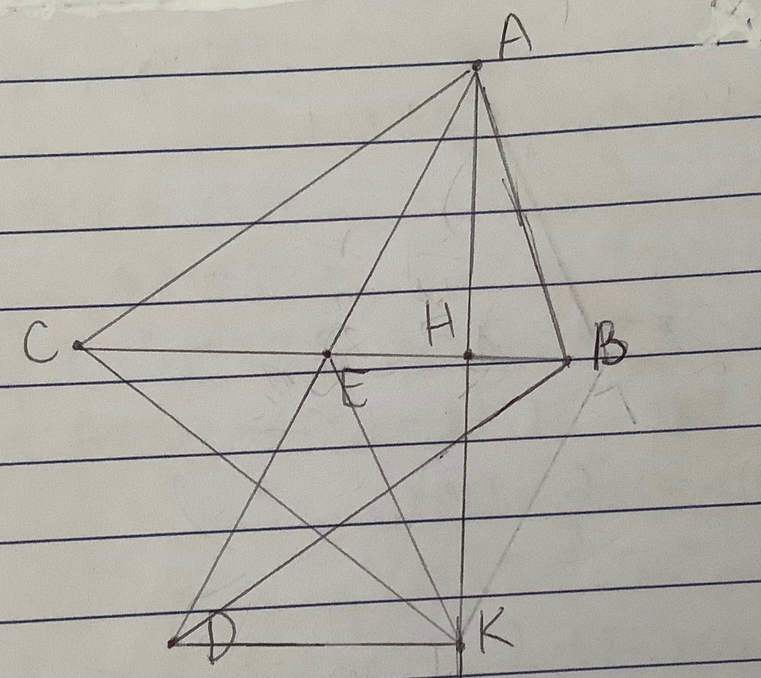
Ta có:\(AH=HK\left(gt\right);AE=ED\left(gt\right)\Rightarrow\)EH là đường trung bình trong tam giác AKD⇒EH//DK⇒BC//DK
Nối BK và CP
Xét ΔBEK và ΔCED có:
\(BE=CE\left(gt\right)\)
\(\widehat{BEK}=\widehat{CED}\left(=\widehat{BEA}\right)\)
\(EK=ED\left(=AE\right)\)
⇒ΔBEK = ΔCED (c.g.c)
⇒KE=DE (2 cạnh tương ứng)
⇒ΔDEK cân tại E⇒\(\widehat{EKD}=\widehat{EDK}\)
ΔBEK = ΔCED (cmt)⇒\(\widehat{BEK}=\widehat{CED}\)
Ta có: \(\widehat{BEK}+\widehat{KED}+\widehat{CED}=180^o\Rightarrow2\widehat{BEK}=180^o-\widehat{KED}\)(1)
Xét ΔKED có:\(\widehat{KED}+\widehat{EKD}+\widehat{EDK}=180^o\Rightarrow2\widehat{EKD}=180^o-\widehat{KED}\)(2)
Từ (1) và (2)⇒\(2\widehat{BEK}=2\widehat{EKD}\Rightarrow\widehat{BEK}=\widehat{EKD}\)
Mà 2 góc này là 2 góc so le trong ⇒BE//KD⇒BC//KD