Luyện tập về ba trường hợp bằng nhau của tam giác

1. Hai tam giác bằng nhau

- Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Ví dụ: Nếu \(\Delta ABC=\Delta DEF\) thì \(\left\{{}\begin{matrix}AB=DE;AC=DF;BC=EF\\\widehat{A}=\widehat{D};\widehat{B}=\widehat{E};\widehat{C}=\widehat{F}\end{matrix}\right.\)

- Kí hiệu: Người ta quy ước khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo đúng thứ tự.

Ví dụ: \(\Delta ABC=\Delta A'B'C'\) thì \(\widehat{A}=\widehat{A'};\widehat{B}=\widehat{B'};\widehat{C}=\widehat{C'}\)

2. Trường hợp bằng nhau thứ nhất của tam giác (cạnh - cạnh - cạnh) (c.c.c)

- Tính chất: Nếu ba cạnh của một tam giác này lần lượt bằng ba cạnh của một tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ: Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có:

          \(AB=A'B'\)

          \(BC=B'C'\)

          \(AC=A'C'\)

 thì \(\Delta ABC=\Delta A'B'C'\) (c.c.c)

3. Trường hợp bằng nhau thứ hai của tam giác (cạnh - góc - cạnh) (c.g.c)

- Tính chất: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ: Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có:

         \(AB=A'B'\)

         \(\widehat{B}=\widehat{B'}\)

         \(BC=B'C'\)

       thì \(\Delta ABC=\Delta A'B'C'\) (c.g.c)

- Hệ quả: Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Hệ quả này chính là được suy ra từ trường hợp cạnh - góc - cạnh nêu trên.

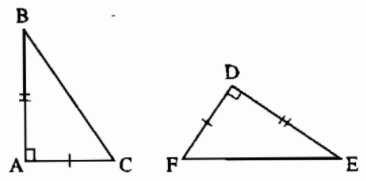
Ví dụ: Nếu \(\Delta ABC\) và \(\Delta DEF\) có:

          \(\widehat{A}=\widehat{D}=90^0\)

          \(AB=DE\)

          \(AC=DF\)

      thì \(\Delta ABC=\Delta DEF\) 

4. Trường hợp bằng nhau thứ ba của tam giác (góc - cạnh - góc) (g.c.g)

- Tính chất: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

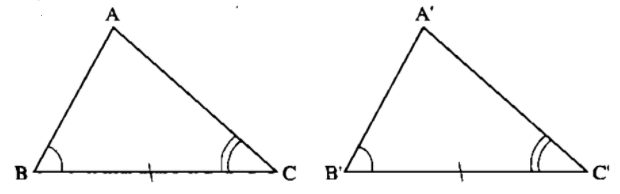
Ví dụ: Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có:

         \(BC=B'C'\)

         \(\widehat{B}=\widehat{B'}\)

         \(\widehat{C}=\widehat{C'}\)

   thì \(\Delta ABC=\Delta A'B'C'\) (g.c.g)

- Hệ quả:

+ Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

+ Hệ quả 2: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.