Bài 6: Tam giác cân

1. Tam giác cân

Định nghĩa:

Tam giác cân là tam giác có hai cạnh bằng nhau.

Trong hình vẽ dưới đây: 

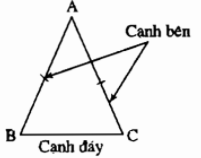
Tam giác \(ABC\) có \(AB=AC\), ta nói tam giác \(ABC\) là một tam giác cân.

Trong đó, \(AB\), \(AC\) là các cạnh bên, \(BC\) là cạnh đáy; \(\widehat{B}\),\(\widehat{C}\) là các góc ở đáy, \(\widehat{A}\) là góc ở đỉnh.

Ta còn nói: Tam giác \(ABC\) cân tại \(A\).

Ví dụ: Tam giác \(DEF\) có \(DE=DF=5\). Ta nói tam giác \(DEF\)cân tại \(D\)

Trong đó: \(DE,DF\) là các cạnh bên, \(EF\) là cạnh đáy

                \(\widehat{D}\) là góc ở đỉnh , \(\widehat{E},\widehat{F}\) là các góc ơ đáy.

Xét ví dụ sau (hình vẽ): Kể tên các tam giác cân trong hình vẽ sau:

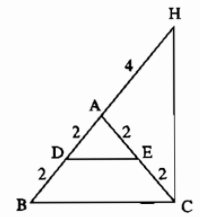
+) \(\Delta ADE\) cân tại \(A\) (do \(AD=AE=2\)). Có \(AD,AE\) là các cạnh bên, \(DE\) là cạnh đáy. \(\widehat{A}\) là góc ở đỉnh, \(\widehat{D},\widehat{E}\) là các góc ở đáy.

+) \(\Delta ABC\) cân tại \(A\) (do \(AB=AC=2+2=4\)). Có \(AB,AC\) là các cạnh bên, \(BC\) là cạnh đáy. \(\widehat{A}\)  là góc ở đỉnh, \(\widehat{B},\widehat{C}\) là các góc ở đáy.

+) \(\Delta ACH\) cân tại \(A\) (do \(AC=AH=4\)). Có \(AC,AH\) là các cạnh bên, \(CH\) là cạnh đáy, \(\widehat{A}\) là góc ở đỉnh, \(\widehat{C},\widehat{H}\) là các góc ở đáy.

Tính chất

Định lí 1) Trong một tam giác cân, hai góc ở đáy bằng nhau.

Định lí 2) Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

Ví dụ: Nếu tam giác \(ABC\) cân tại \(A\) thì \(\widehat{B}=\widehat{C}\) 

          Ngược lại: Nếu tam giác \(ABC\) có \(\widehat{B}=\widehat{C}\) thì tam giác \(ABC\) là một tam giác cân (tại A).

Ta đã biết rằng \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) mà \(\widehat{B}=\widehat{C}\) \(\Rightarrow\) \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}\) 

và \(\widehat{A}=180^0-2.\widehat{B}\left(=180^0-2.\widehat{C}\right)\)

Có thể khái quát thành công thức tính như sau: trong một tam giác cân:

Số đo góc ở đỉnh = \(180^0\) - 2.Số đo một góc ở đáy

Số đo góc ở đáy = (\(180^0\) - Số đo góc ở đỉnh) : 2

Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Ví dụ: Tam giác \(ABC\) vuông tại \(A\) có \(AB=AC\) thì tam giác \(ABC\) là một tam giác vuông cân.

Xét trong tam giác trên ta thấy:

Do trong tam giác cân hai góc ở đáy bằng nhau \(\Rightarrow\widehat{B}=\widehat{C}\)  (1)

Lại có trong tam giác vuông hai góc nhọn phụ nhau \(\Rightarrow\widehat{B}+\widehat{C}=90^0\)  (2)

Từ (1) và (2) \(\Rightarrow\widehat{B}=\widehat{C}=\dfrac{90^0}{2}=45^0\)

Nhận xét: Trong tam giác vuông cân, hai góc nhọn bằng nhau và bằng \(45^0\).

2. Tam giác đều

Định nghĩa:

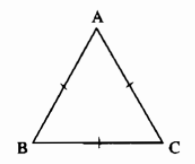
Tam giác đều là tam giác có ba cạnh bằng nhau.

Hình minh hoạ:

Từ định lí 1) và định lí 2) nêu trên ta có thể suy ra các tính chất:

- Trong một tam giác đều, mỗi góc bằng \(60^0\).

- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

- Nếu một tam giác cân có một góc bằng \(60^0\) thì tam giác đó là tam giác đều.