Bài 7: Định lí Pitago

1. Định lí Py-ta-go

Định lí:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Ví dụ: Tam giác \(ABC\) vuông tại \(A\), cạnh \(BC\) là cạnh huyền, \(AB,AC\) là các cạnh góc vuông. Áp dụng định lí 

Py-ta-go vào tam giác \(ABC\)  ta được: \(AB^2+AC^2=BC^2\)

 Ví dụ:

+) Tam giác \(MNP\) vuông tại \(P\) thì \(MP^2+NP^2=MN^2\)

+) Tam giác \(DEF\) vuông tại \(D\) thì \(DE^2+DF^2=EF^2\).

Để làm rõ hơn về định lí trên, ta xét một số bài tập ví dụ sau:

Ví dụ 1: Cho tam giác \(ABC\) vuông tại \(B\) có \(AC=10\), \(BC=8\). Tính \(AB\)?

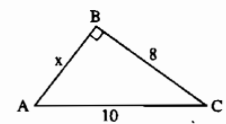
Áp dụng định lí Pytago ta được: \(AB^2+BC^2=AC^2\)

\(\Rightarrow x^2+8^2=10^2\) \(\Rightarrow x^2=10^2-8^2=100-64=36\)

\(\Rightarrow x=6\)

Vậy \(AB=6\).

Ví dụ 2: Tam giác \(DEF\) vuông cân tại \(D\) có độ dài cạnh góc vuông là \(1\). Tính độ dài cạnh huyền của tam giác đó?

Do tam giác \(DEF\) vuông cân tại \(D\) \(\Rightarrow DE=DF=1\)

Áp dụng định lí Py-ta-go ta được: \(DE^2+DF^2=EF^2\)

\(\Rightarrow1^2+1^2=EF^2\) \(\Rightarrow EF^2=2\) \(\Rightarrow EF=\sqrt{2}\)

Vậy độ dài cạnh huyền của tam giác đó là \(\sqrt{2}\).

2. Định lí Py-ta-go đảo

Định lí đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

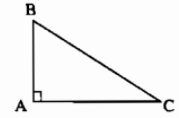
Tam giác \(ABC\) có \(AB^2+AC^2=BC^2\) thì tam giác \(ABC\) là một tam giác vuông (tại \(A\)).

Ví dụ:

+) Tam giác \(HIK\) có \(HI^2+IK^2=HK^2\) thì tam giác \(HIK\) là một tam giác vuông (tại \(I\))

+) Tam giác \(MNP\) có \(MN^2+NP^2=MP^2\) thì tam giác \(MNP\) là một tam giác vuông (tại \(N\))

Xét bài tập ví dụ sau: Một tam giác có độ dài 3 cạnh là \(3cm\), \(5cm\) \(7cm\). Hỏi đó có phải là một tam giác vuông không? Vì sao?

Bài giải:

Để giải được bài toán này, ta cần áp dụng Định lí Py-ta-go đảo.

Tuy nhiên, ta biết rằng trong tam giác vuông, cạnh huyền luôn lớn hơn cạnh góc vuông.

Do đó ta không cần thử tất cả các trường hợp mà chỉ cần thử xem bình phương của cạnh lớn nhất có bằng tổng các bình phương của hai cạnh còn lại hay không.

Ta có: \(7^2=49\)

          \(3^2+5^2=9+25=34\)

Ta thấy rằng \(49\ne34\) nên độ dài 3 cạnh của tam giác này không thoả mãn định lí Py-ta-go

Suy ra tam giác trên không phải là tam giác vuông.