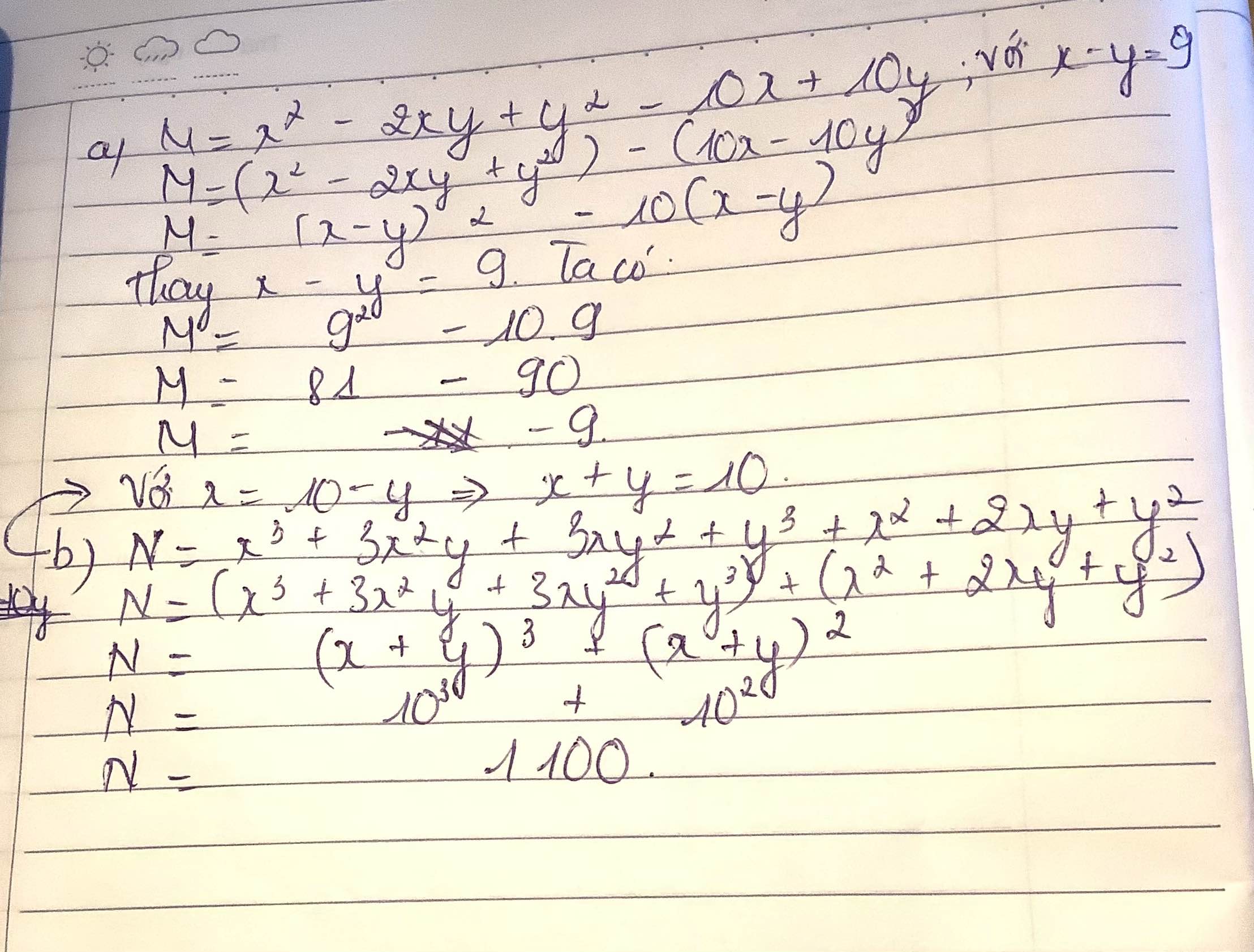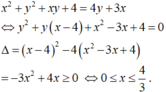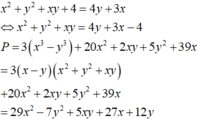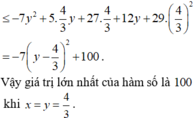tìm x,y thuộc N sao cho x3-x2-2xy=y3+y2+100

Những câu hỏi liên quan
tìm x,y thuộc N* sao cho x3+y3+4(x2+y2)+4(x+y)=16xy
Tính giá trị biểu thức:
a) M=x2-2xy+y2-10x+10y với x-y=9
b) N=x3+3x2y+3xy2+y3+x2+2xy+y2 với x=10-y
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
Đúng 1
Bình luận (0)
a) Cho x+y=9,xy=18 tính x3+y3, x4+y4,x3-y3
b)Cho x+y = -9 ,tính A= x2+2xy+y2-6x-5y-5
Lời giải:
a.
$x^3+y^3=(x+y)^3-3xy(x+y)=9^3-3.9.18=243$
$x^4+y^4=(x^2+y^2)^2-2x^2y^2=[(x+y)^2-2xy]^2-2x^2y^2$
$=[9^2-2.18]^2-2.18^2=1377$
Nếu $x\geq y$ thì:
$x^3-y^3=(x-y)(x^2+xy+y^2)$
$=|x-y|[(x+y)^2-xy]=\sqrt{(x+y)^2-4xy}[(x+y)^2-xy]$
$=\sqrt{9^2-4.18}(9^2-18)=189$
Nếu $x< y$ thì $x^3-y^3=-189$
b.
$A=(x+y)^2-6(x+y)+y-5$
$=(-9)^2-6(-9)+y-5=130+y$
Chưa đủ cơ sở để tính biểu thức.
Đúng 1
Bình luận (1)
a) \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=9^3-3\cdot18\cdot9=243\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=\left[\left(x+y\right)^2-2xy\right]^2-2\left(xy\right)^2\)
\(=\left(9^2-2\cdot18\right)^2-2\cdot18^2\)
\(=45^2-2\cdot324\)
=1377
Đúng 0
Bình luận (0)
c) 3x + 3y – x2 – 2xy – y2 d) x3 – x + 3x2y + 3xy2 – y + y3
c) \(3x+3y-x^2-2xy-y^2=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)d) \(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\)
\(=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)
Đúng 3
Bình luận (0)
\(c,=3\left(x+y\right)-\left(x+y\right)^2=\left(3-x-y\right)\left(x+y\right)\\ d,=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
Đúng 2
Bình luận (0)
c) \(=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)
d) \(\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]=\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
Đúng 2
Bình luận (0)
Mình đang cần gấp! Giúp mình với ạ
Bài 3: Chứng minh rằng:
a) (x+y+z)2= x2+y2+z2+2xy+2xz+2yz
b) (x-y).(x2+y2+z2-xy-yz-xz)= x3+y3+z3-3xyz
c) (x+y+z)3= x3+y3+z3+3.(x+y).(y+z).(z+x)
Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
Đúng 1
Bình luận (0)
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé
Đúng 1
Bình luận (0)
c,
(\(x\) + y + z)3
=(\(x\) + y)3 + 3(\(x\) + y)2z + 3(\(x\)+y)z2 + z3
= \(x^3\) + 3\(x^2\)y + 3\(xy^{2^{ }}\) + y3 + 3(\(x\)+y)z(\(x\) + y + z) + z3
= \(x^3\) + y3 + z3 + 3\(xy\)(\(x\) + y) + 3(\(x+y\))z(\(x+y+z\))
= \(x^3\) + y3 + z3 + 3(\(x\) + y)( \(xy\) + z\(x\) + yz + z2)
= \(x^3\) + y3 + z3 + 3(\(x\) + y){(\(xy+xz\)) + (yz + z2)}
= \(x^3\) + y3 + z3 + 3(\(x\) + y){ \(x\)( y +z) + z(y+z)}
= \(x^3\) + y3 + z3 + 3(\(x\) + y)(y+z)(\(x+z\)) (đpcm)
Đúng 0
Bình luận (0)
Cho x 10 – y. Khi đó khẳng định nào sau đây là đúng khi nói về giá trị của biểu thức
N
x
3
+
3
x
2
y
+
3
x
y
2
+
y
3
+
x
2
+...
Đọc tiếp
Cho x = 10 – y. Khi đó khẳng định nào sau đây là đúng khi nói về giá trị của biểu thức N = x 3 + 3 x 2 y + 3 x y 2 + y 3 + x 2 + 2 x y + y 2
A. N > 1200
B. N < 1000
C. N < 0
D. N > 1000
Ta có
N = x 3 + 3 x 2 y + 3 x y 2 + y 3 + x 2 + 2 x y + y 2 = ( x 3 + 3 x 2 y + 3 x y 2 + y 3 ) + ( x 2 + 2 x y + y 2 ) = ( x + y ) 3 + ( x + y ) 2 = ( x + y ) 2 ( x + y + 1 )
Từ đề bài x = 10 – y ó x + y = 10. Thay x + y = 10 vào N = ( x + y ) 2 (x + y + 1) ta được
N = 10 2 (10 + 1) = 1100
Suy ra N > 1000 khi x = 10 – y
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy (1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P1√1+x2 +1√1+y2 +4xy−x2−y2
Đọc tiếp
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy =(1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P=1√1+x2 +1√1+y2 +4xy−x2−y2
Không nhìn thấy bất cứ chữ nào của đề bài cả
Đúng 1
Bình luận (0)
a)cho x+y=3 và x2+y2=5.Tính x3+y3
b)x-y=5 và x2+y2=15.Tính x3-y3
a) Ta thấy \(xy=\dfrac{\left(x+y\right)^2-\left(x^2+y^2\right)}{2}=\dfrac{3^2-5}{2}=2\)
\(\Rightarrow x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)\) \(=3\left(5-2\right)=9\)
b) Ta thấy \(xy=\dfrac{-\left(x-y\right)^2+\left(x^2+y^2\right)}{2}=\dfrac{15-5^2}{2}=-5\)
\(\Rightarrow x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)\) \(=5\left(15-5\right)=50\)
Đúng 2
Bình luận (0)
Cho x,y là hai số thực thỏa mãn điều kiện
x
2
+
y
2
+
x
y
+
4
4
y
+
3
x
. Tìm giá trị lớn nhất của biểu thức
P
3
(
x...
Đọc tiếp
Cho x,y là hai số thực thỏa mãn điều kiện x 2 + y 2 + x y + 4 = 4 y + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 ( x 3 - y 3 ) + 20 x 2 + 2 x y + 5 y 2 + 39 x .
![]()
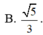
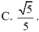
![]()
Cho x+y= 1 tính giá trị biểu thức 2(x3 + y3) - 3( x2 + y2)+100
`2(x^3+y^3)-3(x^2+y^2)+100`
`=2(x+y)(x^2-xy+y^2)-3x^2-3y^2+100`
`=2x^2-2xy+2y^2-3x^2-3y^2+100`
`=-x^2-2xy-y^2+100`
`=-(x+y)^2+100`
`=-1+100=99`
Đúng 1
Bình luận (0)