không giải phương trình, hãy tính: x2 + 9x - 13 = 0 thỏa mãn:
x12x2 + x1x22
1. Giải phương trình: 2x4 - 3x2 - 5 = 0
2. Cho phương trình bậc 2 ẩn x: x2 - (m+5)x-m+6=0 (1) (m là tham số)
a. Giải pt (1) khi m = 1
b. Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa mãn: x12x2 + x1x22 = 18
#help me, hứa sẽ vote.
Bài 1:
$2x^4-3x^2-5=0$
$\Leftrightarrow (2x^4+2x^2)-(5x^2+5)=0$
$\Leftrightarrow 2x^2(x^2+1)-5(x^2+1)=0$
$\Leftrightarrow (x^2+1)(2x^2-5)=0$
$\Leftrightarrow 2x^2-5=0$ (do $x^2+1\geq 1>0$ với mọi $x\in\mathbb{R}$)
$\Leftrightarrow x^2=\frac{5}{2}$
$\Leftrightarrow x=\pm \sqrt{\frac{5}{2}}$
Bài 2:
a. Khi $m=1$ thì pt trở thành:
$x^2-6x+5=0$
$\Leftrightarrow (x^2-x)-(5x-5)=0$
$\Leftrightarrow x(x-1)-5(x-1)=0$
$\Leftrightarrow (x-1)(x-5)=0$
$\Leftrightarrow x-1=0$ hoặc $x-5=0$
$\Leftrightarrow x=1$ hoặc $x=5$
b.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta=(m+5)^2-4(-m+6)\geq 0$
$\Leftrightarrow m^2+14m+1\geq 0(*)$
Áp dụng định lý Viet:
$x_1+x_2=m+5$
$x_1x_2=-m+6$
Khi đó:
$x_1^2x_2+x_1x_2^2=18$
$\Leftrightarrow x_1x_2(x_1+x_2)=18$
$\Leftrightarrow (m+5)(-m+6)=18$
$\Leftrightarrow -m^2+m+12=0$
$\Leftrightarrow m^2-m-12=0$
$\Leftrightarrow (m+3)(m-4)=0$
$\Leftrightarrow m=-3$ hoặc $m=4$
Thử lại vào $(*)$ thấy $m=4$ thỏa mãn.
cho pt:x2-(m+5)x-m+6=0
a.giải pt với m=1
b.tìm các giá trị của m để pt có nghiệm x=-2
c.tìm các giá trị của m để pt có nghiệm x1,x2 thỏa mãn x12x2+x1x22=24
a: Khi m=1 thì pt sẽ là x^2-6x+5=0
=>x=1; x=5
b: Khi x=-2 thì pt sẽ là;
(-2)^2+2(m+5)-m+6=0
=>2m+10-m+6+4=0
=>m=-20
c: =>x1x2(x1+x2)=24
=>(-m+6)(m+5)=24
=>-m^2-5m+6m+30-24=0
=>-m^2+m+6=0
=>m^2-m-6=0
=>m=3; m=-2
a)
Thế m = 1 vào phương trình được: \(x^2-\left(1+5\right)x-1+6=x^2-6x+5=0\)
nhẩm nghiệm a + b + c = 0 ( 1 - 6 + 5 = 0) nên \(x_1=1,x_2=\dfrac{c}{a}=5\)
Vậy hệ phương trình có tập nghiệm \(S=\left\{1;5\right\}\)
b)
Phương trình có nghiệm x = -2
=> \(\left(-2\right)^2-\left(m+5\right).\left(-2\right)-m+6=0\)
<=> \(4+2m+10-m+6=0\)
<=> \(m+20=0\Rightarrow m=-20\)
c) Tìm các giá trị của m để phương trình có 2 nghiệm hay 2 nghiệm phân biệt ... ?
Cho phương trình x2 - 2 ( m - 1)x + 2m - 5 =0
Tìm m để 2 nghiệm thỏa mãn x12x2 - 2mx1 + 30 = 5x2
Cho phương trình 2x2+9x-6=0 hai nghiệm x1,x2. Không giải phương trình, hãy tính giá trị của biểu thức B=4x12+4x22 +5x1*x2
Áp dụng Viét có: `{(x_1+x_2=-b/a=-9/2),(x_1.x_2=c/a=-3):}`
Ta có:`B=4(x_1 ^2+x_2 ^2)+5x_1.x_2`
`<=>B=4(x_1+x_2)^2-8x_1.x_2+5x_1.x_2`
`<=>B=4(-9/2)^2-3.(-3)`
`<=>B=90`
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 + 9x + 7 = 0
2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
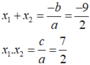
gọi x1,x2 là 2 nghiệm của phương trình \(3x^2+5X-6=0\) không giải phương trình hãy lập phương trình bậc hai ẩn y có 2 nghiệm y1,y2 thỏa mãn y1=2x1-x2 và y2=2x2-x1
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_1+y_2=2x_1-x_2+2x_2-x_1\\y_1y_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1+x_2\\y_1y_2=-2x_1^2-2x_2^2+5x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2\left(x_1+x_2\right)^2+9x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2.\left(-\dfrac{5}{3}\right)^2+9.\left(-2\right)=-\dfrac{212}{9}\end{matrix}\right.\)
\(\Rightarrow y_1;y_2\) là nghiệm của:
\(y^2+\dfrac{5}{3}y-\dfrac{212}{9}=0\Leftrightarrow9y^2+10y-212=0\)
Cho phương trình x2 - (m + 5) x -m + 6=0(1),m là tham số ! a) giải phương trình (1) khi m = 0 /b) tìm m để phương trình có 2 nghiệm x1 x2 thỏa mãn : 2x¹+3x²=13
a: Khi m=0 thì (1) sẽ là x^2-5x+6=0
=>x=2 hoặc x=3
b: 2x1+3x2=13 và x1+x2=m+5
=>2x1+2x2=2m+10 và 2x1+3x2=13
=>x2=13-2m-10=3-2m và x1=m+5-3+2m=3m+2
x1x2=-m+6
=>(-2m+3)(3m+2)=-m+6
=>-6m^2-4m+9m+6=-m+6
=>-6m^2+6m=0
=>m=0 hoặc m=1
Tìm giá trị thực của tham số m để phương trình 9 x - 2 . 3 x + 1 + m = 0 có hai nghiệm thực x 1 , x 2 thỏa mãn x 1 + x 2 = 0
A. m = 6
B. m = 0
C. m = 3
D. m = 1
Cho phương trình (ẩn x) : x 2 – 2mx – 4m – 4 = 0(1)
b) Tìm m để phương trình (1) có 2 nghiệm x 1 , x 2 thỏa mãn x 1 2 + x 2 2 - x 1 x 2 = 13 = 13
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
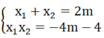
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
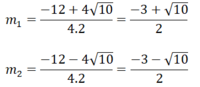
Vậy với 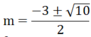 thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13