1,Áp dụng định lý Pi-ta-go vào tam giác vuông AHB ta có:
\(AH^2+BH^2+AB^2\\ \Rightarrow x^2+4^2=\sqrt{52^2}\\ \Rightarrow x^2+16=52\\ \Rightarrow x^2=36\\ \Rightarrow x=6\left(vì.x>0\right)\)

Áp dụng định lý Pi-ta-go vào tam giác vuông AHC ta có:

\(AH^2+HC^2=AC^2\\ \Rightarrow6^2+9^2=y^2\\ \Rightarrow36+81=y^2\\ \Rightarrow117=y^2\\ \Rightarrow y=\sqrt{117}\left(vì.y>0\right)\)

2,Ta có BC=BH+HC=4+9=13

Ta có:\(AB^2+AC^2=\sqrt{52^2}+\sqrt{117^2}=52+117=169\)

\(BC^2=13^2=169\)

\(\Rightarrow AB^2+AC^2=BC^2\)

\(\Rightarrow\Delta ABC\) vuông tại A (định lý Pt-ta-go đảo) 

a. Áp dụng định lý pitago vào tam giác vuông ABH

\(AB^2=AH^2+BH^2\)

\(\Rightarrow x=\sqrt{AB^2-BH^2}=\sqrt{\sqrt{52^2}-4^2}=\sqrt{52-16}=\sqrt{36}=6cm\)

Áp dụng định lý pitago vào tam giác vuông ACH

\(AC^2=AH^2+HC^2\)

\(\Rightarrow y=\sqrt{6^2+9^2}=\sqrt{117}=3\sqrt{13}\)

b. ta có: BC = 13 cm

AB = \(\sqrt{52}cm\)

\(AC=\sqrt{117}cm\)

Ta có: \(BC^2=AB^2+AC^2\)

\(13^2=\sqrt{52^2}+\sqrt{117^2}\)

\(169=169\) ( đúng )

Vậy tam giác ABC là tam giác vuông ( pitago đảo ) và vuông tại A

a. -△IEC có: AF//IC \(\Rightarrow\dfrac{EF}{AE}=\dfrac{EI}{EC}\)

-△IEC có: AM//EI \(\Rightarrow\dfrac{EI}{AC}=\dfrac{AM}{AC}=\dfrac{EF}{AE}\)

\(\Rightarrow AM.AE=EF.AC\).

b. -△AMC và △EFA có:

\(\widehat{MAC}=\widehat{FEA}\)

\(\widehat{ACM}=\widehat{EAF}\)

\(\Rightarrow\)△AMC∼△EFA (g-g)

\(\Rightarrow\dfrac{S_{AMC}}{S_{EFA}}=\left(\dfrac{AM}{EF}\right)^2=\left(\dfrac{6}{2}\right)^2=9\)

\(\Rightarrow S_{AMC}=9S_{EFA}\)

c. -Qua D kẻ đg song song với BC cắt AM, AC tại H,G.

-△ABM có:DH//BM \(\Rightarrow\dfrac{DH}{BM}=\dfrac{AH}{AM}\)

-△ACM có:GH//CM \(\Rightarrow\dfrac{GH}{CM}=\dfrac{AH}{AM}=\dfrac{DH}{BM}\Rightarrow GH=DH\)

\(\Rightarrow\)H là t/đ DG.

-△EDG có: AH//ED, H t/đ DG \(\Rightarrow\)A t/đ EG.

-△EDG có: AF//DG, A t/đ EG\(\Rightarrow\)F t/đ ED.

\(\Rightarrow EF=FD\)

Bài 4:

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có

AB=AC

\(\widehat{KAC}\) chung

Do đó:ΔABH=ΔACK

Suy ra: BH=CK

b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có

BC chung

KC=HB

Do đó: ΔKBC=ΔHCB

Suy ra: \(\widehat{OCB}=\widehat{OBC}\)

hay ΔOBC cân tại O

Xét ΔABO và ΔACO có

AB=AC
BO=CO

AO chung

Do đó: ΔABO=ΔACO

Suy ra: \(\widehat{BAO}=\widehat{CAO}\)

hay AO là tia phân giác của góc BAC

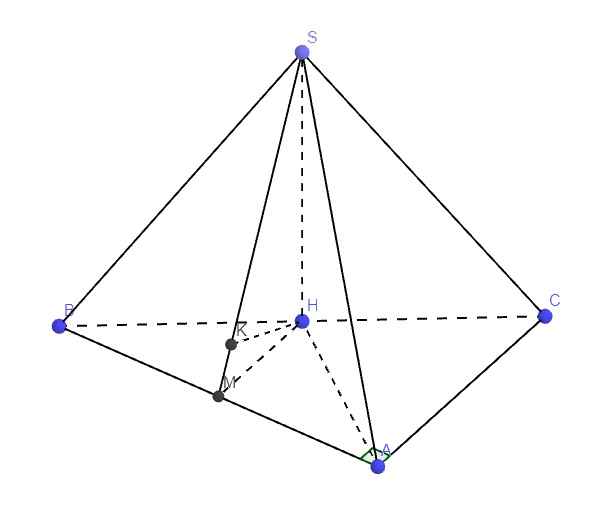
a.

\(SH\perp\left(ABC\right)\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)

\(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\Rightarrow\Delta SBH\) vuông tại H

\(BH=\dfrac{1}{2}BC=a\Rightarrow SH=\sqrt{SB^2-BH^2}=a\sqrt{3}\)

\(SH\perp\left(ABC\right)\Rightarrow HA\) là hình chiếu vuông góc của SA lên (ABC)

\(\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)

\(AH=\dfrac{1}{2}BC=a\) (trung tuyến ứng với cạnh huyền)

\(\Rightarrow tan\widehat{SAH}=\dfrac{SH}{AH}=\sqrt{3}\Rightarrow\widehat{SAH}=60^0\)

b.

H là trung điểm BC, M là trung điểm AB \(\Rightarrow MH\) là đường trung bình tam giác ABC

\(\Rightarrow MH||AC\Rightarrow MH\perp AB\) (do \(AB\perp AC\))

Lại có \(SH\perp\left(ABC\right)\Rightarrow SH\perp AB\)

\(\Rightarrow AB\perp\left(SMH\right)\)

Mà \(AB=\left(SAB\right)\cap\left(ABC\right)\Rightarrow\widehat{SMH}\) là góc giữa (SAB) và (ABC)

\(AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\) \(\Rightarrow MH=\dfrac{1}{2}AC=\dfrac{a\sqrt{3}}{2}\) (đường trung bình)

\(\Rightarrow tan\widehat{SMH}=\dfrac{SH}{MH}=2\Rightarrow\widehat{SMH}\approx63^023'\)

c.

Theo cmt: \(\left\{{}\begin{matrix}MH\perp SH\\MH\perp AB\end{matrix}\right.\) \(\Rightarrow MH\) là đường vuông góc chung của SH và AB

\(\Rightarrow d\left(SH;AB\right)=MH=\dfrac{a\sqrt{3}}{2}\)

Từ H kẻ HK vuông góc SM (K thuộc SM)

\(AB\perp\left(SMH\right)\Rightarrow AB\perp HK\)

\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)

Hệ thức lượng trong tam giác vuông SMH:

\(HK=\dfrac{SH.MH}{\sqrt{SH^2+MH^2}}=\dfrac{a\sqrt{15}}{5}\)

b1 x khác 4

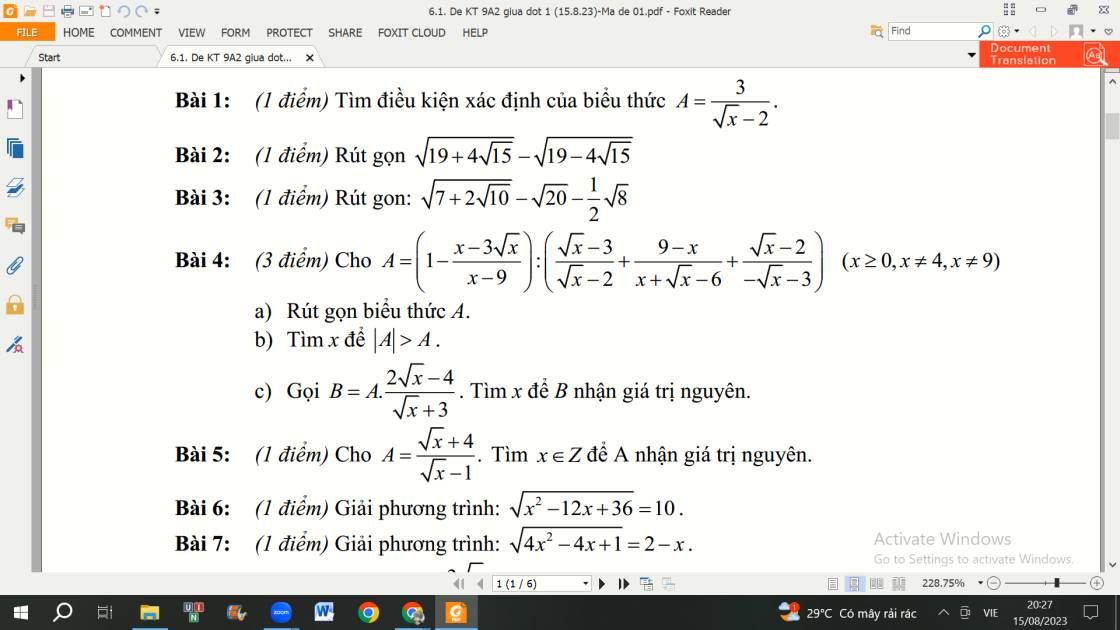
4:

a: \(A=\left(\dfrac{x-9-x+3\sqrt{x}}{x-9}\right):\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)

\(=\dfrac{3\sqrt{x}-9}{x-9}:\left(\dfrac{x-9+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\right)\)

\(=\dfrac{3\left(\sqrt{x}-3\right)}{x-9}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}=\dfrac{-3}{\sqrt{x}-2}\)

b: |A|>A

=>A<0

=>\(\dfrac{-3}{\sqrt{x}-2}< 0\)

=>căn x-2>0

=>x>4

c: \(B=\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\cdot\dfrac{-3}{\left(\sqrt{x}-2\right)}=\dfrac{-6}{\sqrt{x}+3}\)

Để B là số nguyên thì \(\sqrt{x}+3\inƯ\left(-6\right)\)

=>\(\sqrt{x}+3\in\left\{3;6\right\}\)

=>\(x\in\left\{0;9\right\}\)

mà x<>9

nên x=0

Em cập nhật lại đề nha em!