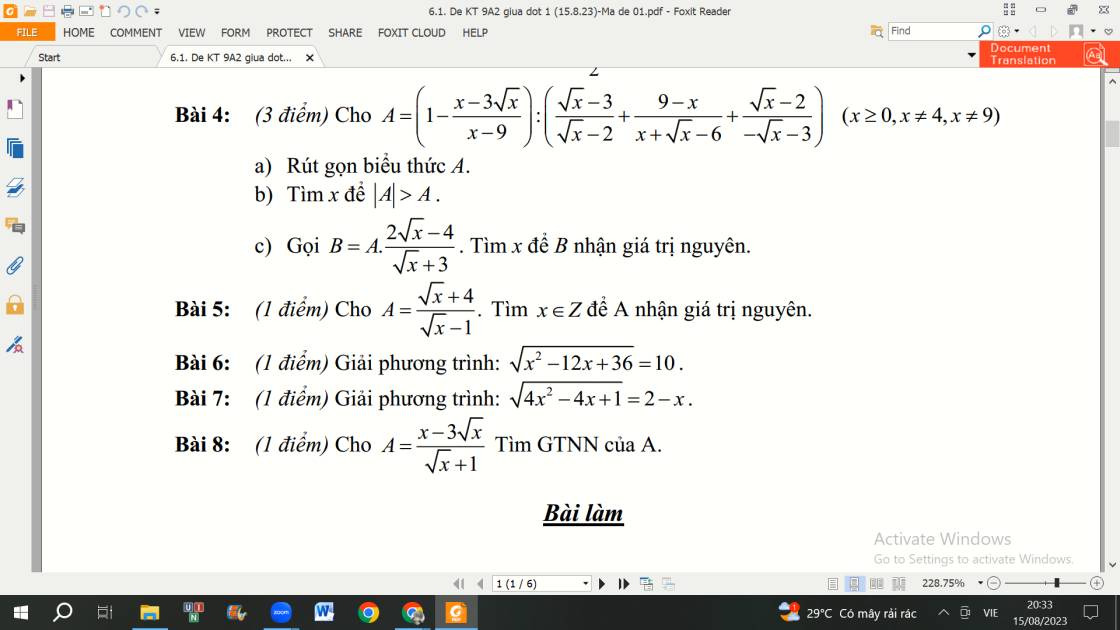
4:
a: \(A=\left(\dfrac{x-9-x+3\sqrt{x}}{x-9}\right):\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\sqrt{x}-9}{x-9}:\left(\dfrac{x-9+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{x-9}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}=\dfrac{-3}{\sqrt{x}-2}\)
b: |A|>A
=>A<0
=>\(\dfrac{-3}{\sqrt{x}-2}< 0\)
=>căn x-2>0
=>x>4
c: \(B=\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\cdot\dfrac{-3}{\left(\sqrt{x}-2\right)}=\dfrac{-6}{\sqrt{x}+3}\)
Để B là số nguyên thì \(\sqrt{x}+3\inƯ\left(-6\right)\)
=>\(\sqrt{x}+3\in\left\{3;6\right\}\)
=>\(x\in\left\{0;9\right\}\)
mà x<>9
nên x=0

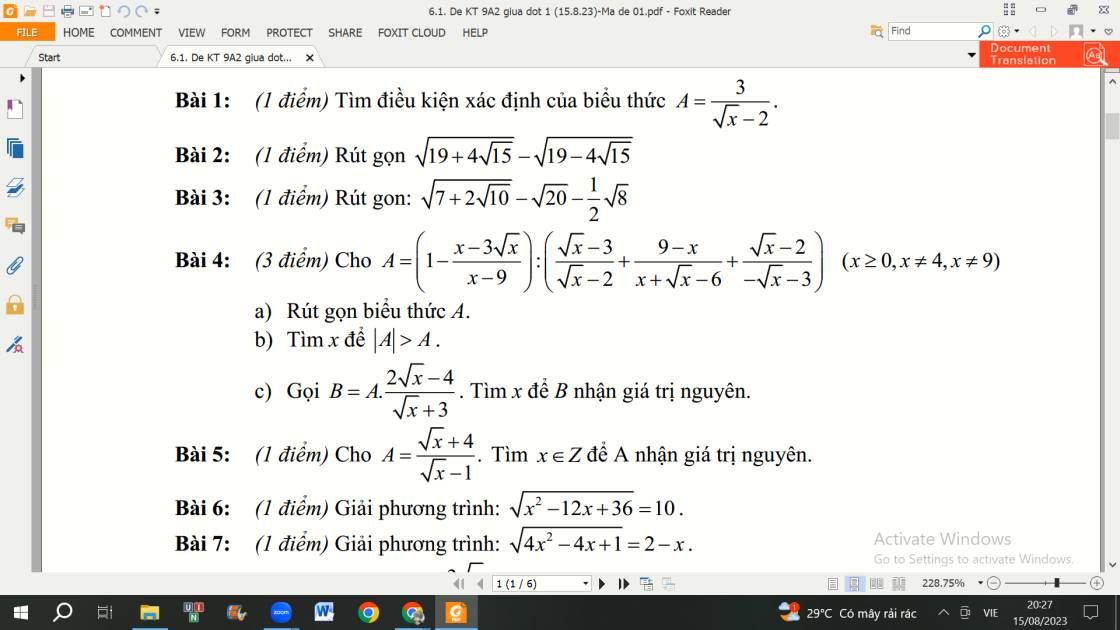








 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn