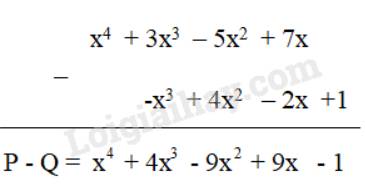chứng minh rằng 2 không là nghiệm của đa thức M(x)=x4+3x3-5x2+7x+2

Những câu hỏi liên quan
bài 11: cho đa thức F(x)=-x+2+5x2+2x4+2x3+x2+x4
G(x)=-x2+x3+x-6-3x3-4x2-3x4
a. thu gọn các đa thức trên theo thu gọn phổ biến
b.Tính F(x)+G(x);F(x)-G(x)
c. tìm nghiệm của đa thức F(x)+G(x)
a: f(x)=3x^4+2x^3+6x^2-x+2
g(x)=-3x^4-2x^3-5x^2+x-6
b: H(x)=f(x)+g(x)
=3x^4+2x^3+6x^2-x+2-3x^4-2x^3-5x^2+x-6
=x^2-4
f(x)-g(x)
=3x^4+2x^3+6x^2-x+2+3x^4+2x^3+5x^2-x+6
=6x^4+4x^3+11x^2-2x+8
c: H(x)=0
=>x^2-4=0
=>x=2 hoặc x=-2
Đúng 0
Bình luận (0)
Câu 12. Đa thức x4 - 3x3 + 6x2 - 7x + m chia hết cho đa thức x - 1 khi m bằng.
A. 0 B. -3 C. 3 D. 1
Câu 20: Phân tích đa thức 5x2(x-2y)-15x(x-2y) thành nhân tử ta được
A.5x(x-2y) B. x(x-2y)(x-3)
C.5x(x-2y)(x-3) D.5(x-2y)(x-3)
Bài 3 (1,75 điểm): Cho hai đa thức: A(x) 3x6+ 3x3 - 3x3 - 3x6 - x3 + x4 + 2023
B(x) x3 + x2 -1
a. Thu gọn và sắp xếp đa thức A(x) theo luỹ thừa giảm của biến.
b. Tính A(x) + B(x)
c. Biết H(x) – A(x) B(x). Chứng minh đa thức H(x) không có nghiệm
Bài 4 (3điểm): Cho ABC vuông tại A. Tia phân giác của góc ABC cắt AC ở D.Kẻ
DH BC
a. Chứng minh ABD HBD
b. Gọi I là giao điểm của 2 tia BA và HD. Chứng minh IDC cân.
c. Chứng minh: AD +AI 1
2
IC
ét o ét cíu vs mn
Đọc tiếp
Bài 3 (1,75 điểm): Cho hai đa thức: A(x) = 3x6+ 3x3 - 3x3 - 3x6 - x3 + x4 + 2023 B(x) = x3 + x2 -1 a. Thu gọn và sắp xếp đa thức A(x) theo luỹ thừa giảm của biến. b. Tính A(x) + B(x) c. Biết H(x) – A(x) = B(x). Chứng minh đa thức H(x) không có nghiệm Bài 4 (3điểm): Cho ABC vuông tại A. Tia phân giác của góc ABC cắt AC ở D.Kẻ DH BC a. Chứng minh ABD = HBD b. Gọi I là giao điểm của 2 tia BA và HD. Chứng minh IDC cân. c. Chứng minh: AD +AI > 1 2 IC
ét o ét cíu vs mn
Xem thêm câu trả lời
F(x)=-x+2+5x2+2x4+2x3+x2+x4
G(x)=-x2+x3+x-6-3x3-4x2-3x4
a. thu gọn các đa thức trên
\(F\left(x\right)=3x^4+2x^3+6x^2-x+2\)
\(G\left(x\right)=-3x^4-2x^3-5x^2+x-6\)
Đúng 5
Bình luận (0)
F(x)=-x+2+5x2+2x4+2x3+x2+x4
F(x)= ( 5x2+x2) + ( 2x4 +x4) +2x3-x+2
F (x) = 6x2 + 3x4 +2x3-x+2
G(x) = -x2+x3+x-6-3x3-4x2-3x4
G (x) = ( -x2 -4x2) + ( x3 -3x3) -3x4 +x-6
G (x) = -5x2 - 2x3 -3x4 +x-6
Đúng 0
Bình luận (0)
Bài 1. Chứng minh rằng:
a) Chứng tỏ rằng 3/2 và -1/3 là các nghiệm của đa thức P(x)=6x2 -7x- 3
b) Chứng tỏ rằng -1/2 và 3 là các nghiệm của đa thức 2x2 -5x- 3
a: 6x^2-7x-3=0
=>6x^2-9x+2x-3=0
=>(2x-3)(3x+1)=0
=>x=-1/3 hoặc x=3/2
=>ĐPCM
b: 2x^2-5x-3=0
=>2x^2-6x+x-3=0
=>(x-3)(2x+1)=0
=>x=-1/2 hoặc x=3
=>ĐPCM
Đúng 0
Bình luận (0)
Cho 2 đa thức : P(x)=3x3−x2−2x4+3+2x3+x+3x4−x2−2x4+3+2x3+x+3x4 và Q(x)=−x4+x2=4x3−2+2x2−x−x3−x4+x2=4x3−2+2x2−x−x3
a) Thu gọn và sắp xếp hai đa thức P(x) và Q(x) theo lũy thừa giảm dần của biến;
b) Tính P(x) + Q(x)
c) Chứng tỏ rằng đa thức H(x)=P(x)+Q(x) không có nghiệm
Giúp mik nha
a) \(P\left(x\right)=3x^3-x^2-2x^4+3+2x^3+x+3x^4-x^2-2x^4+3+2x^3+x+3x^4\)
\(=2x^4+7x^3-2x^2+2x+6\)
\(Q\left(x\right)=-x^4+x^2-4x^3-2+2x^2-x-x^3-x^4+x^2-4x^3-2+2x^2-x-x^3\)
\(=-2x^4-10x^3+6x^2-2x-4\)
b) \(P\left(x\right)+Q\left(x\right)=2x^4+7x^3-2x^2+2x+6-2x^4-10x^3+6x^2-2x-4\)
\(=-3x^3+4x^2+2\)
Đúng 0
Bình luận (0)
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Ta có: P – Q = x4 + 3x3 – 5x2 + 7x – (-x3 + 4x2 – 2x +1)
= x4 + 3x3 – 5x2 + 7x + x3 - 4x2 - 4x2 + 2x – 1
= x4 + (3x3+ x3 ) + (– 5x2 - 4x2 ) + (7x + 2x ) – 1
= x4 + 4x3 – 9x2 + 9x – 1
Đúng 1
Bình luận (0)
1/ Cho 2 đa thức:
P(x) =x4-7x2+x-2x3+4x2+6x-2
Q(x)=x4-3x-5x3+x+1+6x3
a/ Thu gọn rồi sắp xếp các đa thức trên theo lũy thừa giảm của biến
b/ Chứng minh: x=2 là nghiệm của P(x) nhưng không là nghiệm của Q(x)
GIÚP MÌNH VỚI MN ><
a) Thu gọn:
P(x) = x4+(-7x2+4x2)+(x+6x)-2x3-2
P(x) = x4-3x2+7x-2x3-2
Sắp xếp: P(x) = x4-2x3-3x2+7x-2
Thu gọn:
Q(x) = x4+(-3x+x)+(-5x3+6x3)+1
Q(x) = x4-2x+x3+1
Sắp xếp: Q(x)= x4+ x3-2x+1
b/ Nếu x=2, ta có:
P(2) = 24-2.23-3.22+7.2-2
= 16 - 2.8 - 3.4 + 14 -2
= 16-16-12+14-2
= -12+14-2
= 0
=> x=0 là nghiệm của P(x)
Q(2)= 24+ 23-2.2+1
= 16+8-4+1
= 24-4+1
=21
mà 21≠0
Vậy: x=2 không phải là nghiệm của Q(x)
=>
Đúng 0
Bình luận (0)