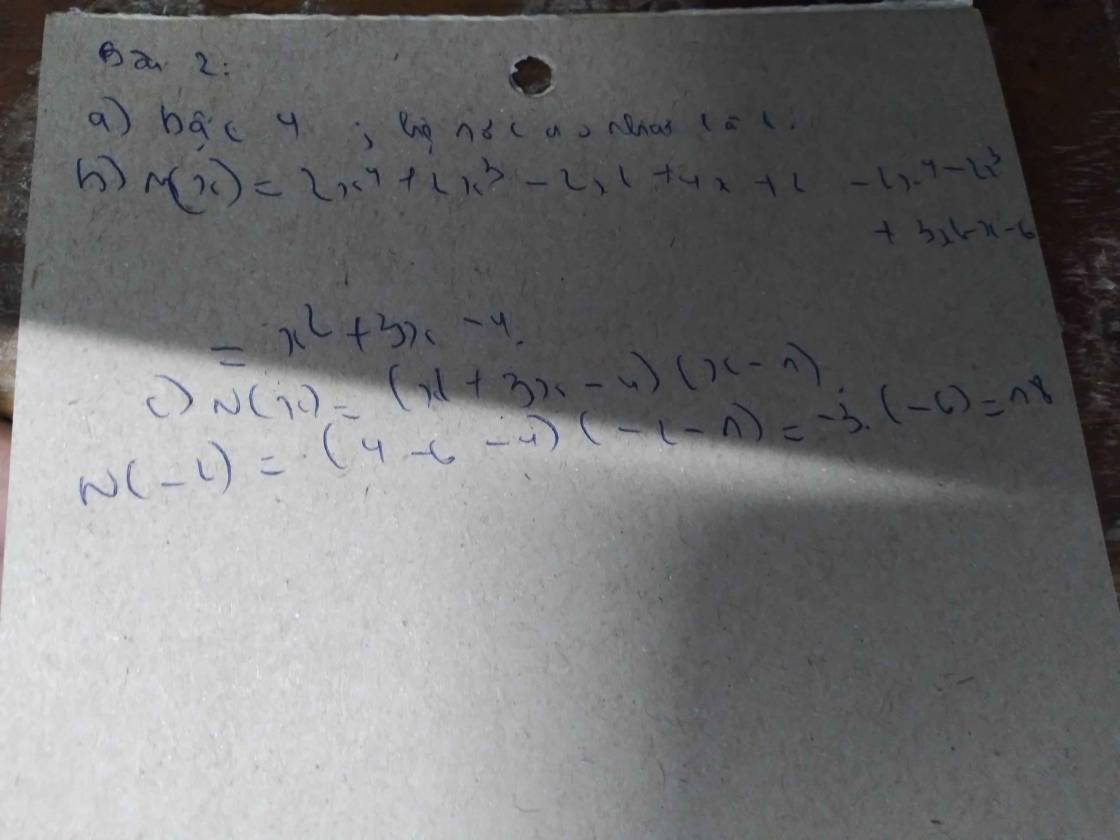Ôn tập chương Biểu thức đại số

\(=\dfrac{\left(x-1\right)\cdot\left(x^2+x+1\right)}{x-1}=x^2+x+1\)

`(x^3-1):(x-1)`

`=(x-1)(x^2+x+1):(x-1)`

`=x^2+x+1`

=(x-3)(x^2+3x+2)

=x^3+3x^2+2x-3x^2-9x-6

=x^3-7x-6

(x+7)^2+2023>=2023 với mọi x

Dấu = xảy ra khi x=-7

Câu 1:

a) A(x) = 2x² - 7 + 4x³ + 2x - 5x²

= 4x³ + (2x² - 5x²) + 2x - 7

= 4x³ - 3x² + 2x - 7

Bậc của A(x) là 3

b) Thay x = -2 vào đa thức P(x) = 4 - x², ta có:

P(-2) = 4 - (-2)² = 0

Vậy x = -4 là một nghiệm của P(x)

Câu 3:

a) A(x) = -4x + 7 + x² + 5x³

= 7 - 4x + x² + 5x³

B(x) = 5x - 5x³ + x² - 3

= -3 + 5x + x² - 5x³

*) Đa thức A(x) có:

- Bậc 3

- Hệ số cao nhất: 5

- Hệ số tự do: 7

*) Đa thức B(x) có:

- Bậc 3

- Hệ số cao nhất: -5

- Hệ số tự do: -3

b) P(x) = B(x) - A(x)

= (-3 + 5x + x² - 5x³) - (7 - 4x + x² + 5x³)

= -3 + 5x + x² - 5x³ - 7 + 4x - x² - 5x³

= (-5x³ - 5x³) + (x² - x²) + (5x + 4x) + (-3 - 7)

= -10x³ + 9x - 10

Q(x) = 2A(x) - 3B(x)

= 2(7 - 4x + x² + 5x³) - 3(-3 + 5x + x² - 5x³)

= 14 - 8x + 2x² + 10x³ + 9 - 15x - 3x² + 15x³

= (10x³ + 15x³) + (2x² - 3x²) + (-8x - 15x) + (14 + 9)

= 25x³ - x² - 23x + 23

c) Thay x = -2 vào P(x) ta có:

P(-2) = -10.(-2)³ + 9.(-2) - 10

= 80 - 18 - 10

= 52

Vậy giá trị của P(x) là 52 tại x = -2

Câu 2:

a) M(x) = 3x + x² - 6x³ - 9

= -6x³ + x² + 3x - 9

b) N(x) - M(x) = 4x³ - 5x + 2

N(x) = (4x³ - 5x + 2) + M(x)

= (4x³ - 5x + 2) + (-6x³ + x² + 3x - 9)

= 4x³ - 5x + 2 - 6x³ + x² + 3x - 9

= (4x³ - 6x³) + x² + (-5x + 3x) + (2 - 9)

= -2x³ + x² - 2x - 7

a: =(9x^2+6x)/3x=3x+2

b: =(2x^2-4x+x-2)/[-(x-2)]

=-2x-1

a.

\(x^4+2x^2+7=x^4+2x^2-24+31=\left(x^2+6\right)\left(x^2-4\right)+31\)

\(=\left(x^2+6\right)\left(x-2\right)\left(x+2\right)+31\)

Vậy \(x^4+2x^2+7\) chia \(x+2\) được \(\left(x^2+6\right)\left(x-2\right)\) dư \(31\)

b.

\(x^2+10x+a=x^2+10x+21+a-21=\left(x+3\right)\left(x+7\right)+a-21\)

\(\Rightarrow x^2+10x+a\) chia hết \(x+3\) khi và chỉ khi \(a-21\) chia hết \(x+3\) với mọi x

\(\Rightarrow a-21=0\)

\(\Rightarrow a=21\)

Lời giải:
$2x^3-4x^2+a-10=2x^2(x-2)+a-10$

$\Rightarrow$ để $2x^3-4x^2+a-10$ chia hết cho $x-2$ thì $a-10=0$
$\Leftrightarrow a=10$

D(x)=0

=>x-3=0 hoặc 2x+5=0

=>x=3 hoặc x=-5/2