chỉ cho mk cách làm bài này với
cho hàm số :y=-2x+1/3
A(0; 1/3) có thuộc đồ thị hàm số không
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
chỉ cho mk cách làm bài này với
cho hàm số :y=-2x+1/3
A(0;1/3) có thuộc đồ thị hàm số không
Thay x=0 vào y=-2x+1/3, ta được:
y=-2x0+1/3=1/3
Vậy: A(0;1/3) có thuộc đồ thị hàm số y=-2x+1/3
Tìm m để đường thẳng (d): \(y=mx+4\) tiếp xúc với đồ thị hàm số (P): \(\dfrac{-x^2}{4}\) .
(hai đồ thị hàm số tiếp xúc nhau là hai đồ thị chỉ có 1 điểm chung)
Giúp mk làm bài này với
Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{4}x^2-mx-4=0\)
\(\Leftrightarrow x^2+4mx+16=0\)
\(\Delta=\left(4m\right)^2-4\cdot1\cdot16=16m^2-64\)
Để hai đồ thị tiếp xúc với nhau thì 16m2-64=0
=>m=2 hoặc m=-2
Bài này mình làm ko ra mọi người chỉ cách làm giúp mình với!!!
Tìm m để hàm số y= (2m+1)Sinx + (3-m)x đồng biến trên R?\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm
Bài 1
Cho hàm số y=2x+1
a, vẽ đồ thị của hàm số
b, Tính góc tạo bởi đường thẳng y=2x +1 với trục Õ (làm tròn đến phút )
c. xác định hàm số y = ax + b (a khác 0) biết đồ thị hàm số đi qua điểm M(1;-2) và song song với đồ thị hàm số đã cho
Cho hàm số y=\(\dfrac{2x+m}{\sqrt{x-2m-1}-3}\)
Tìm m để hàm số xác định trên khoảng (0;+vô cùng). trình bày cách làm rõ nhá
100% group làm sai
Cho bài toán: “Xét tính đơn điệu của hàm số y = x 2 + 2 x - 3 ” Một bạn học sinh đã làm bài như sau:
Bước 1: Tập xác định: D = ℝ \ ( - 3 ; 1 )
Bước 2: Tìm đạo hàm: y ' = x 2 + 2 x - 3 ' 2 x 2 + 2 x - 3 = x + 1 x 2 + 2 x - 3
Bước 3: y ' = 0 ⇔ x + 1 = 0 x 2 + 2 x - 3 > 0 ⇔ x = 1 x < - 3 ⇔ x ∈ ∅ ; x > 1
Bước 4: Bảng biến thiên:
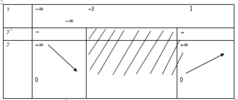
Bước 5: Kết luận:
Vậy hàm số nghịch biến trên nửa khoảng ( - ∞ ; - 3 ] , đồng biến trên nửa khoảng [ 1 ; + ∞ ) . Hỏi bài làm trên đúng hay
sai? Nếu sai thì sai từ bước nào?
A. Bài làm đúng.
B. Sai từ bước 3.
C. Sai từ bước 4.
D. Sai từ bước 5
Cho hàm số y= ( 3-2m) .x + m-1 (1) với m là tham số a) Vẽ đồ thị hàm số với m =1 b) Hàm số (1) cắt 2x -3=0 tại 1 điểm trên trục hoành ( Giúp mk vói mk đang cần gấp ạ)
a, với m = 1 thay m = 1 vào hàm số : y = ( 3-2m)x+ m-1 ta có :
y = ( 3-2.1)x+1-1
y = x
Đồ thị hàm số giao với trục Ox tại điểm có tung độ bằng 0 nên; y =0
=> x = 0
Đồ thị hàm số đi qua điểm O(0;0)
với x = 1 => y = 1 .
Đồ thị đi qua A(1;1)
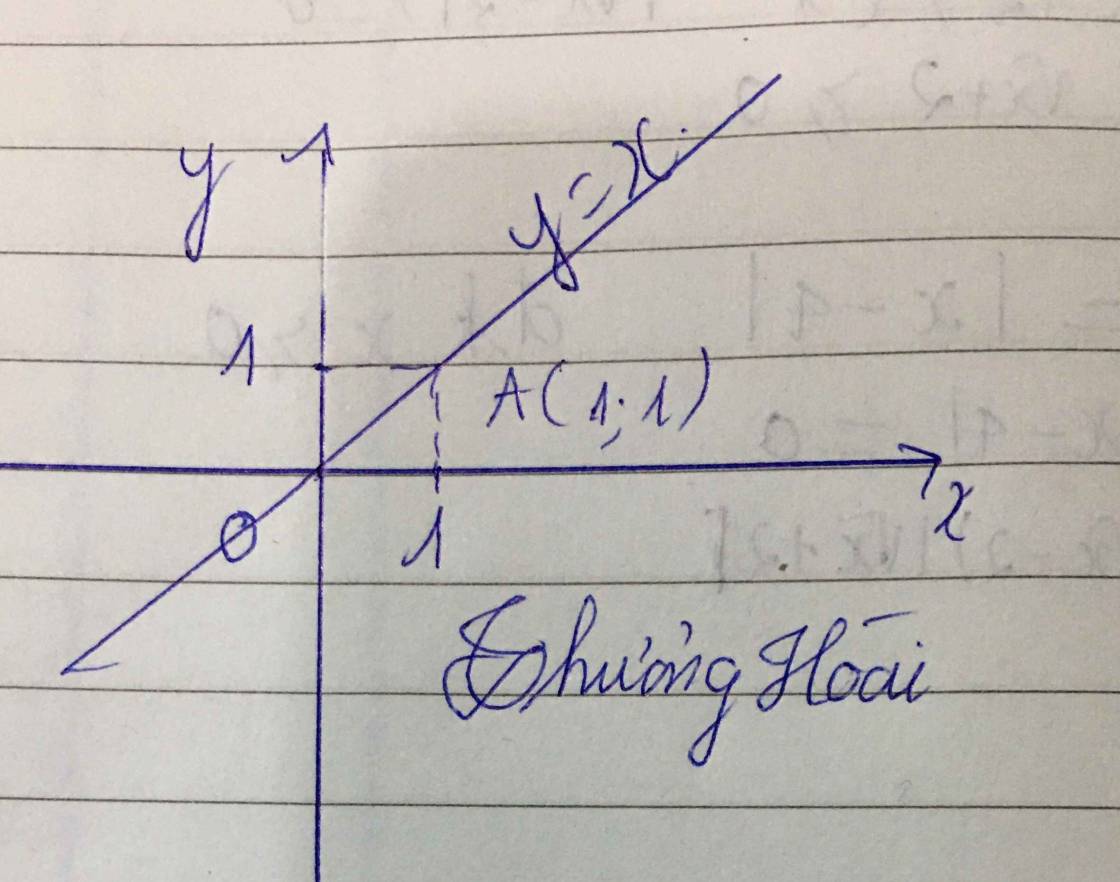
b, Gọi B (x1;y1) là giao điểm của hàm số y= (3-2m)x + m-1và hàm số
2x-3 = 0 .
Theo bài ra ta có: y1 = 0 => (3-2m)x1 + m - 1 = 0
Vì B là giao điểm của hai đt nên tọa độ điểm B thỏa mãn hàm số :
2x - 3 = 0=> 2x1 - 3 = 0 => x1 = 3/2
Thay x1 = 3/2 vào pt (3-2m)x1 +m -1 = 0 ta có :
(3-2m) .3/2 + m - 1 = 0
9/2 - 3m + m - 1 = 0
-2m + 7/2 = 0
m = 7/4
Kết luận với m = 7/4 thì đồ thị hàm số : y =( 3-2m)x+m-1
có dạng : y = -1/2x + 3/4 và giao với đồ thị 2x-3 = 0 tại điểm B( 3/2; 0)
và điểm B nằm trục hoành
Bài 1: Cho hàm số y =f( x)= -5x -1. Tính f(-1), f(0), f(1), f(1/2)
Bài 2: a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f(-1/2); f(1/2).
b) Cho hàm số y = g(x) = x – 1. Tính g(-1); g(0) ; g(1) ; g(2).
c) Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Lm giúp mình vs mình đang cần gấp .
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
a: f(-2)=7
f(-1)=5
f(0)=3
Cho phương trình -2x+3y=7 (1)
Số nghiệm nguyên của (1) thỏa mãn 0<x<y là?
CHỈ CHO MÌNH CÁCH LÀM VỚI
LÀM ĐÚNG MÌNH TICK CHO
\(y>x>0\)\(\Rightarrow7=-2x+3y>-2x+3x=x\)
\(0< x< 7\Rightarrow x\in\left\{1;2;3;4;5;6\right\}\)
\(y=\frac{7+2x}{3}\)
Thay x vào y xem giá trị nào làm y nguyên thì nhận