Thay x=0 vào y=-2x+1/3, ta được:
y=-2x0+1/3=1/3
Vậy: A(0;1/3) có thuộc đồ thị hàm số y=-2x+1/3
Thay x=0 vào y=-2x+1/3, ta được:
y=-2x0+1/3=1/3
Vậy: A(0;1/3) có thuộc đồ thị hàm số y=-2x+1/3
Cho hàm số y = f x . Hàm số y = f ' x có đồ thị như hình vẽ.
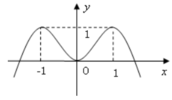
Bất phương trình f x 64 + x + 3 - 2 x + 1 > m đúng với mọi x ∈ 0 ; 1 khi chỉ khi
A. m ≤ f 1 + 16 64
B. m < f 1 + 16 64
C. m ≤ f 0 64 + 1 2 + 3
D. m < f 0 64 + 1 2 + 3
Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình vẽ:
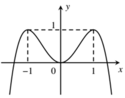
Bất phương trình f x 36 + x + 3 - 2 x - 1 > m đúng với mọi mÎ(0;1) khi và chỉ khi
A. m ≤ f 1 + 9 36
B. m < f 1 + 9 36
C. m > f 1 + 9 36
D. m ≥ f 1 + 9 36
Cho hàm số f x = x 3 - 3 x 2 + 2 x + 1 . Tiếp tuyến của đồ thị hàm số tại điểm M(0;1) có hệ số góc là:
A. -1.
B. 1.
C. 2.
D. 0.
Cho hàm số y = f(x) liên tục và có đạo hàm trên R, có đồ thị như hình vẽ. Với m là tham số bất kỳ thuộc [0;1]. Phương trình f x 3 - 3 x 2 = 3 m + 4 1 - m có bao nhiêu nghiệm thực?
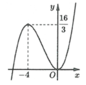
A. 2
B. 3
C. 5
D. 9
Cho hàm số y = f(x) liên tục và có đạo hàm trên ℝ , có đồ thị như hình vẽ. Với m là tham số bất kì thuộc [0;1]. Phương trình f x 3 - 3 x 2 = 3 m + 4 1 - m có bao nhiêu nghiệm thực?
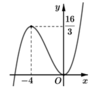
A. 2
B. 3
C. 5
D. 9
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C). Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C)
A. 0
B. 3
C. 2
D. 1
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Gọi M là điểm có hoành độ dương thuộc đồ thị hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất. Tọa độ điểm M là
A. 4 ; 3
B. 0 ; − 1
C. 1 ; − 3
D. 3 ; 5