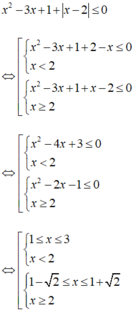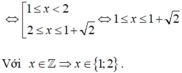tập nghiệm của bất phương trình \(2< \left|5-x\right|\le7\) có bao nhiêu số nguyên

Những câu hỏi liên quan
Cho phương trình \(log_2\left(-x^2+4x+m\right)\)+\(log_{\dfrac{1}{2}}\left(x^2+2\right)\)< \(log_23\). Có bao nhiêu giá trị nguyên của tham số m sao cho bất phương trình đã cho nghiệm đúng mọi x thuộc [1;5]
ĐKXĐ: \(-x^2+4x+m>0\)
\(log_2\left(-x^2+4x+m\right)-log_2\left(x^2+2\right)< log_23\)
\(\Leftrightarrow log_2\left(\dfrac{-x^2+4x+m}{x^2+2}\right)< log_23\)
\(\Leftrightarrow\dfrac{-x^2+4x+m}{x^2+2}< 3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x^2+4x+m>0\\-x^2+4x+m< 3x^2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>x^2-4x\\m< 4x^2-4x+6\end{matrix}\right.\) ; \(\forall x\in\left[1;5\right]\)
Xét hai hàm \(\left\{{}\begin{matrix}f\left(x\right)=x^2-4x\\g\left(x\right)=4x^2-4x+6\end{matrix}\right.\) trên \(\left[1;5\right]\) ta được: \(\left\{{}\begin{matrix}f\left(x\right)_{max}=f\left(5\right)=5\\g\left(x\right)_{min}=g\left(1\right)=6\end{matrix}\right.\)
\(\Rightarrow5\le m\le6\)
Có 2 giá trị nguyên của m
Đúng 2
Bình luận (0)
a) Cho hai số thực a và b thỏa a-b2. Tích a và b đạt Min bằng bao nhiêu b) Có bao nhiêu giá trị nguyên của x thuộc [-2;5] thỏa mãn phương trình x2(x-1) ge0c) Bất pt left|4x+3right|-left|x-1right| x có tập nghiệm S(a;b). Tính giá trị biểu thức P2a-4bd) Có bao nhiêu giá trị nguyên của tham số m để bất phương trình x^2-2mx+2left|x-mright|+20
Đọc tiếp
a) Cho hai số thực a và b thỏa a-b=2. Tích a và b đạt Min bằng bao nhiêu
b) Có bao nhiêu giá trị nguyên của x thuộc [-2;5] thỏa mãn phương trình x2(x-1) \(\ge0\)
c) Bất pt \(\left|4x+3\right|-\left|x-1\right|< x\) có tập nghiệm S=(a;b). Tính giá trị biểu thức P=2a-4b
d) Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \(x^2-2mx+2\left|x-m\right|+2>0\)
Bất phương trình \(x^2-2\left|x-1\right|+2>0\) có bao nhiêu nghiệm nguyên thuộc khoảng (-20; 30)
Bất phương trình \(\dfrac{2x^2-x-1}{\left|x+1\right|-2x}\le-2x^2+x+1\) có bao nhiêu nghiệm nguyên?
Tập nghiệm của bất phương trình
x
2
-
3
x
+
1
+
x
-
2
≤
0
có tất cả bao nhiêu số nguyên? A. Vô số B. 4 C. 2 D. 3
Đọc tiếp
Tập nghiệm của bất phương trình x 2 - 3 x + 1 + x - 2 ≤ 0 có tất cả bao nhiêu số nguyên?
A. Vô số
B. 4
C. 2
D. 3
Tập tập nghiệm của bất phương trình
log
1
2
x
+
2
≥
-
2
có chứa bao nhiêu số nguyên A. Vô số B. 5 C. 4 D. 6
Đọc tiếp
Tập tập nghiệm của bất phương trình log 1 2 x + 2 ≥ - 2 có chứa bao nhiêu số nguyên
A. Vô số
B. 5
C. 4
D. 6
Có ![]()
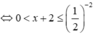
![]() có chứa tất cả 4 số nguyên.
có chứa tất cả 4 số nguyên.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho phương trình \(5^x+m=log_5\left(x-m\right)\) với m là tham số. Có bao nhiêu giá trị nguyên của \(m\in\left(-20;20\right)\) để phương trình đã cho có nghiệm
https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG
bạn tham khảo nha
Đúng 2
Bình luận (0)
Cho S là tập hợp tất cả caccs giá trị nguyên của tham ssos m sao cho bất phương trình \(\dfrac{(m+1)x^2+\left(4m+2\right)x+4m+4}{mx^2+2\left(2m+1\right)x+m}\le1\) có tập nghiệm là R . Tính số phần tử của tập hợp S
tập nghiệm của bất phương trình \(\sqrt{\left(x+5\right)\left(3-x\right)}\le x^2+2x+a\) nghiệm đúng \(\forall x\in\)[5;3] , Tham số a phải thỏa điều kiện gì?
\(\Leftrightarrow\sqrt{-x^2-2x+15}-x^2-2x+15\le a+15\)
Đặt \(\sqrt{-x^2-2x+15}=t\ge0\)
Đồng thời ta có: \(\sqrt{-x^2-2x+15}=\sqrt{\left(x+5\right)\left(3-x\right)}\le\dfrac{1}{2}\left(x+5+3-x\right)=4\)
\(\Rightarrow0\le t\le4\)
BPT trở thành: \(t^2+t\le a+15\Leftrightarrow t^2+t-15\le a\) ; \(\forall t\in\left[0;4\right]\)
\(\Leftrightarrow a\ge\max\limits_{t\in\left[0;4\right]}\left(t^2+t-15\right)\)
Xét hàm \(f\left(t\right)=t^2+t-15\) trên \(\left[0;4\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\notin\left[0;4\right]\) ; \(f\left(0\right)=-15\) ; \(f\left(4\right)=5\)
\(\Rightarrow f\left(t\right)_{max}=4\Rightarrow a\ge4\)
Đúng 1
Bình luận (2)