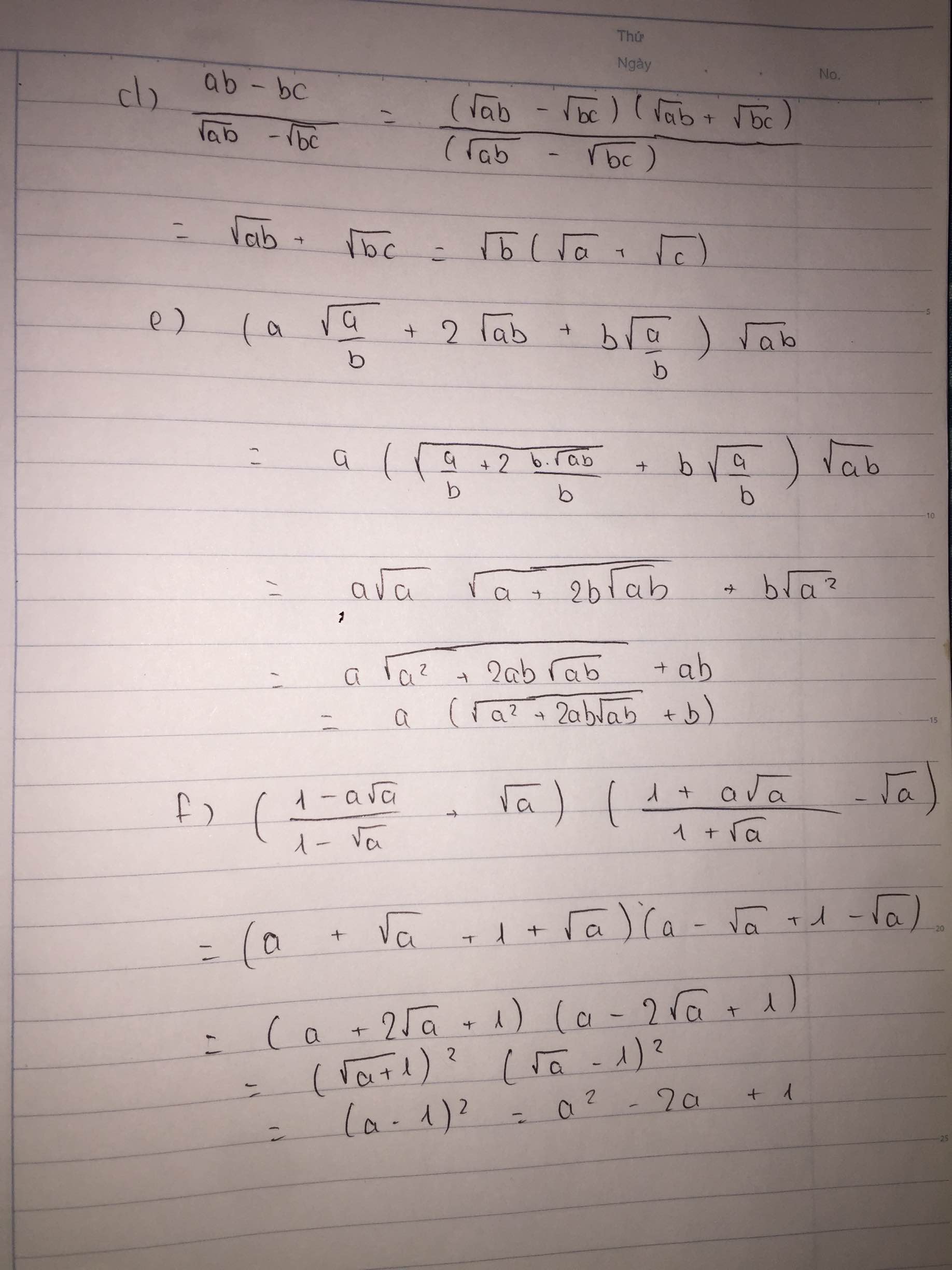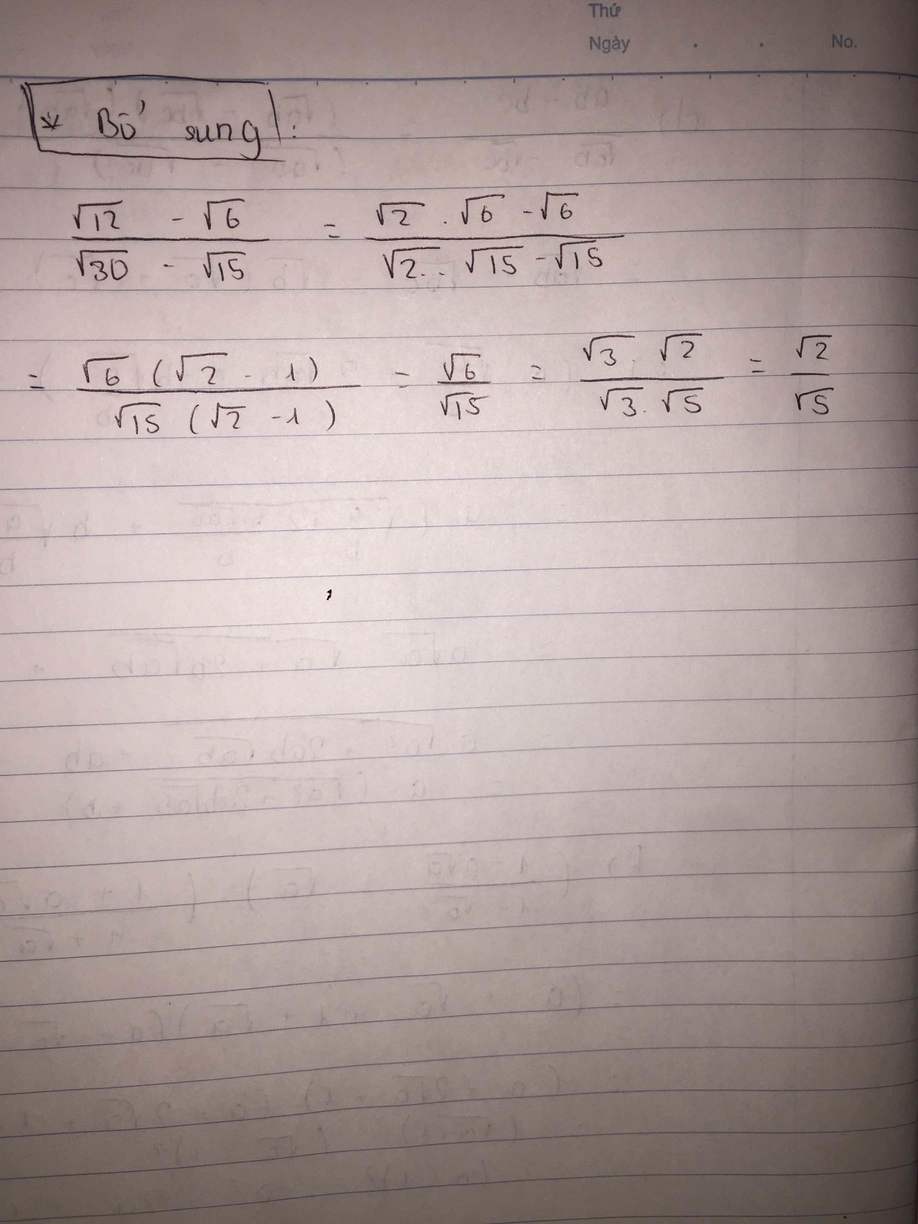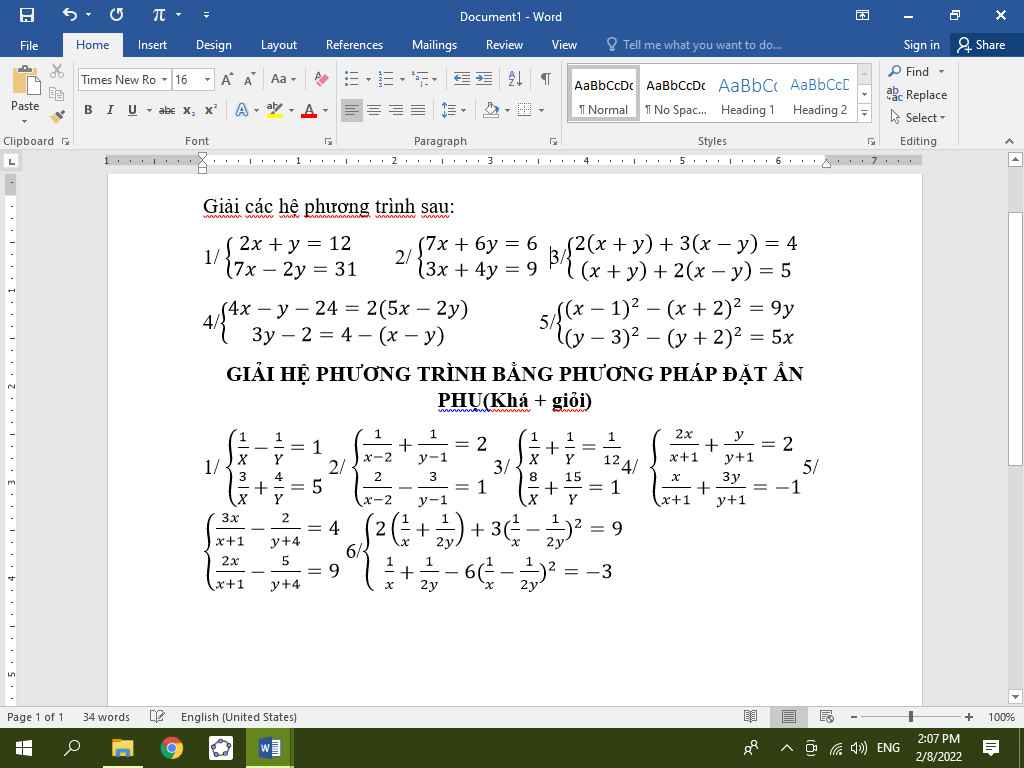
1, \(\left\{{}\begin{matrix}4x+2y=24\\7x-2y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=55\\y=12-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)

2, thiếu đề 

4, \(\left\{{}\begin{matrix}4x-y-24=10x-4y\\3y-2=4-x+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\-6x-12y=-36\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}15y=60\\x=6-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-2\end{matrix}\right.\)

Bài 3:

Gọi K là giao của AH và BC thì AK là đường cao thứ 3 (H là trực tâm)

Vì \(\widehat{BDC}=\widehat{BEC}=90^0\) nên BEDC nội tiếp

Lại có \(BI=IC=ID=IE=\dfrac{1}{2}BC\) (trung tuyến ứng cạnh huyền) nên I là tâm đg tròn ngoại tiếp BDEC

Gọi G là trung điểm AH thì \(AG=GD=DE=\dfrac{1}{2}AH\) (trung tuyến ứng ch)

Do đó G là tâm () ngoại tiếp tg ADE

Vì \(GA=GD\Rightarrow\widehat{DAG}=\widehat{GDA}\)

Vì \(ID=IB\Rightarrow\widehat{ABI}=\widehat{IDB}\)

Do đó \(\widehat{IDB}+\widehat{GDA}=\widehat{DAG}+\widehat{ABI}=90^0\left(\Delta AKB\perp K\right)\)

Do đó \(\widehat{IDG}=180^0-\left(\widehat{IDB}+\widehat{GDA}\right)=90^0\)

Vậy \(ID\perp IG\) hay ...

Gọi 3 số nguyêntố đó là: a, b, c

Ta có: 5(a+b+c)

=>abc chia hết cho 5, do a,b,c nguyên tố

=>chỉ có trường hợp 1 trong 3 số bằng 5, giả sử a=5

=>bc=b+c+5=>(b-1)(c-1)=6

trương hợp 1: b - 1 = 1=>b=2;c - 1 = 6=>c=7

trường hợp 2: b - 1= 2, c - 1 = 3 =>c=4(loại)

vậy 3 số nguyên tố đó là: 2;5;7

sao abc lại ⋮5?

Câu 16:

PTHH: \(Cl_2+2NaOH\rightarrow NaCl+NaClO+H_2O\)

Ta có: \(\left\{{}\begin{matrix}n_{Cl_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\\n_{NaOH}=\dfrac{600\cdot20\%}{40}=3\left(mol\right)\end{matrix}\right.\) \(\Rightarrow\) 2 chất p/ứ hết

Mặt khác: \(m_{Cl_2}=1,5\cdot71=106,5\left(g\right)\)

\(\Rightarrow m_{nướcjaven}=m_{Cl_2}+m_{ddNaOH}=706,5\left(g\right)\)

Câu 21:

PTHH: \(H_2SO_{4\left(đ\right)}+CaF_2\rightarrow CaSO_4+2HF\)

Ta có: \(n_{HF}=\dfrac{250\cdot40\%}{20}=5\left(kmol\right)\) 

\(\Rightarrow n_{CaF_2}=2,5\left(kmol\right)\) \(\Rightarrow m_{CaF_2}=2,5\cdot78=195\left(kg\right)\) 

:vvv nhiều quá v bn gửi lẻ ra đi

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)

\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)

\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)

\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)

\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)

\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)

\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)

\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)

\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)

\(=\left(a-1\right)^2=a^2-2a+1\)

Câu 4: D

Câu 5 : D

Câu 6 : A

a) Có: `1+tan^2a=1/(cos^2a)`

`<=> 1+(3/5)^2=1/(cos^2a)`

`=> cosa=\sqrt10/4`

`=> sina = \sqrt(1-cos^2a) = \sqrt6/4`

b) Có: `sin^2a + cos^2a=1`

`<=> sin^2a + (1/4)^2=1`

`=> sina=\sqrt15/4`

`=> tana = (sina)/(cosa) = \sqrt15`

a) Giả sử tam giác ABC vuông tại B có \(tanA=\dfrac{3}{5}\)

\(\Rightarrow\dfrac{BC}{AB}=\dfrac{3}{5}\Rightarrow BC=\dfrac{3}{5}AB\Rightarrow AC=\sqrt{AB^2+\dfrac{9}{25}AB^2}=\dfrac{\sqrt{34}}{5}AB\)

\(\Rightarrow\dfrac{AB}{AC}=\dfrac{5}{\sqrt{34}}\Rightarrow cosA=\dfrac{5}{\sqrt{34}}\)

\(AC=\dfrac{\sqrt{34}}{5}AB\Rightarrow AC=\dfrac{\sqrt{34}}{5}.\dfrac{5}{3}BC=\dfrac{\sqrt{34}}{3}BC\Rightarrow\dfrac{BC}{AC}=\dfrac{3}{\sqrt{34}}\)

\(\Rightarrow sinA=\dfrac{3}{\sqrt{34}}\)

b) cũng tương tự như câu a thôi,bạn tự tính nha

31B

32C

33B

34 underline "they"?