=>x^2+4x+4-x^2-10x-25<=-8x-10

=>-6x-21<=-8x-10

=>2x<=11

=>x<=11/2

ĐKXĐ: ...

\(\Leftrightarrow\sqrt{\left(x-1\right)\left(x-3\right)}-\sqrt{\left(x-1\right)\left(2x-1\right)}-\left(x-1\right)=0\)

- Với \(x=1\) là 1 nghiệm

- Với \(x\le\frac{1}{2}\)

\(\Leftrightarrow\sqrt{3-x}-\sqrt{1-2x}+\sqrt{1-x}=0\)

\(\Leftrightarrow\sqrt{3-x}+\sqrt{1-x}=\sqrt{1-2x}\)

\(\Leftrightarrow4-2x+2\sqrt{x^2-4x+3}=1-2x\)

\(\Leftrightarrow2\sqrt{x^2-4x+3}=-3\left(vn\right)\)

- Với \(x\ge3\)

\(\Leftrightarrow\sqrt{x-3}-\sqrt{2x-1}-\sqrt{x-1}=0\)

\(\Leftrightarrow\sqrt{x-3}=\sqrt{2x-1}+\sqrt{x-1}\)

\(\Leftrightarrow x-3=3x-2+2\sqrt{2x^2-3x+1}\)

\(\Leftrightarrow2\sqrt{2x^2-3x+1}=-2x-1\left(vn\right)\)

Vậy pt có nghiệm duy nhất \(x=1\)

sao k ai trả lời zậy ta

Nhấn máy tính: 

+ giải hpt x²-4x+3: mode=> 5:EQN=> số 3=> 1=> = => -4 => = => 3=> X₁=3 => = => X₂=1

=> Thay vào=> Đưa vô căn bậc 2.

+ giải hpt 2x² -3x+1 tương tự như trên.

=> Sau đó thay vô. tính ra

Xin lỗi mình chỉ biết nhiêu đây. lớp 7. Thông cảm.

1) ta có: \(x^2\le\left|1-\frac{2}{x^2}\right|\)                            ( *)

+ nếu \(x^2\ge2\)

từ (*) \(\Rightarrow x^2\le1-\frac{2}{x^2}\)

\(\Leftrightarrow x^2-1+\frac{2}{x^2}\le0\)

\(\Rightarrow x^4-x^2+2\le0\)         (vì \(x^2\ge0\))

\(\Leftrightarrow\left(x^2-\frac{1}{4}\right)^2+\frac{7}{4}\le0\)  ( vô lý )

+ nếu \(x^2\le2\)

tứ (*) \(\Rightarrow x^2\le\frac{2}{x^2}-1\)

\(\Leftrightarrow x^2-\frac{2}{x^2}+1\le0\)

\(\Rightarrow x^4-2+x^2\le0\)        (vì \(x^2\ge0\))

\(\Leftrightarrow\left(x^2-1\right)\left(x^2+2\right)\le0\)

\(\Leftrightarrow x^2-1\le0\)      ( vì \(x^2+2\)> 0 )

\(\Leftrightarrow x^2\le1\)

\(\Leftrightarrow-1\le x\le1\)

Vậy: \(-1\le x\le1\)

Ta có : \(\frac{\left|x^2-4x\right|+3}{x^2+\left|x-5\right|}\ge1\)

\(\Leftrightarrow\left|x^2-4x\right|+3\ge x^2+\left|x-5\right|\)

\(\Leftrightarrow\left|x^2-4x\right|+3-x^2-\left|x-5\right|\ge0\)   (1)

+ nếu x= 0. từ pt (1) => 3 \(\ge\)0 ( đúng )

+ nếu x < 4 và x \(\ne\)0.

từ pt (1) => 4x - x²  + 3 - x² - ( 5 - x ) \(\ge\)0

\(\Leftrightarrow-2x^2+5x-2\ge0\)

\(\Leftrightarrow2x^2-5x+2\le0\)

\(\Leftrightarrow\left(x-2\right)\left(2x-1\right)\le0\)

\(\orbr{\begin{cases}\hept{\begin{cases}x-2\ge0\\2x-1\le0\end{cases}}\\\hept{\begin{cases}x-2\le0\\2x-1\ge0\end{cases}}\end{cases}}\)   TH 1: 

\(\hept{\begin{cases}x-2\ge0\\2x-1\le0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge2\\x\le\frac{1}{2}\end{cases}}\)( vô lý ) 

    TH 2:

\(\hept{\begin{cases}x-2\le0\\2x-1\ge0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\le2\\x\ge\frac{1}{2}\end{cases}}\)\(\Leftrightarrow\)\(\frac{1}{2}\le x\le2\)  ( thỏa mãn x< 4 )

+ nếu \(4\le x< 5\)

từ pt (1) => x² - 4x + 3 - x² - ( 5 - x ) \(\ge0\)

\(\Leftrightarrow-3x-2\ge0\)

\(\Leftrightarrow3x+2\le0\)

\(\Leftrightarrow x\le-\frac{2}{3}\)( không thỏa man \(4\le x< 5\))

+ nếu \(x\ge5\)

từ pt (1) => x² - 4x + 3 - x² - ( x -5 ) \(\ge\)0

\(\Leftrightarrow-5x+8\ge0\)

\(\Leftrightarrow5x\le8\)
\(\Leftrightarrow x\le\frac{8}{5}\)  ( không thỏa mãn \(x\ge5\))

vậy: bpt có nghiệm là \(\frac{1}{2}\le x\le2\)

a: \(\Leftrightarrow4\left(4x-2\right)+12\left(-x+3\right)< =3\left(1-5x\right)\)

=>16x-8-12x+36<=3-15x

=>4x+28<=3-15x

=>19x<=-25

hay x<=-25/19

b: \(\Leftrightarrow6\left(x+4\right)+30\left(-x-5\right)>=10\left(x+3\right)-15\left(x-2\right)\)

=>6x+24-30x-150<=10x+30-15x+30

=>-24x-126<=-5x+60

=>-19x<=186

hay x>=-186/19

\(a,\dfrac{4x-2}{3}-x+3\le\dfrac{1-5x}{4}\\ \Leftrightarrow\dfrac{4\left(4x-2\right)}{12}-\dfrac{12\left(x-3\right)}{12}\le\dfrac{3\left(1-5x\right)}{12}\\ \Leftrightarrow16x-8-12x+36\le3-15x\\ \Leftrightarrow4x+28\le3-15x\\ \Leftrightarrow19x+25\le0\\ \Leftrightarrow x\le-\dfrac{25}{19}\)

\(b,\dfrac{x+4}{5}-x-5\ge\dfrac{x+3}{3}-\dfrac{x-2}{2}\\ \Leftrightarrow\dfrac{6\left(x+4\right)}{30}-\dfrac{30\left(x+5\right)}{30}\ge\dfrac{10\left(x+3\right)}{30}-\dfrac{15\left(x-2\right)}{30}\\ \Leftrightarrow6x+24-30x-150\ge10x+30-15x+30\\ \Leftrightarrow-24x-126\ge-5x+60\\ \Leftrightarrow19x+186\le0\\ \Leftrightarrow x\le-\dfrac{186}{19}\)

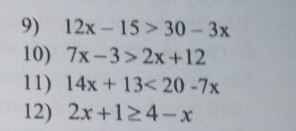
`9)`

`12x-15>30-3x`

`<=>12x+3x>30+15`

`<=>15x>45`

`<=>15x*1/15>45*1/15`

`<=>x>3`

`10)`

`7x-3>2x+12`

`<=>7x-2x>12+3`

`<=>5x>15`

`<=>5x*1/5>15*1/5`

`<=>x>3`

`11)`

`14x+13<20-7x`

`<=>14x+7x<20-13`

`<=>21x<7`

`<=>21x*1/21<7*1/21`

`<=>x<1/3`

`12)`

`2x+1≥4-x`

`<=>2x+x≥4-1`

`<=>3x≥3`

`<=>3x*1/3≥3*1/3`

`<=>x≥1`

9: =>15x>45

=>x>3

10: =>5x>15

=>x>3

11: =>21x<7

=>x<1/3

12: =>3x>=3

=>x>=1

9, 12x-15>30-3x
<=>12x-15+3x>30
<=>15x>45
<=>x>3
10,  7x-3>2x+12
<=>7x-3-2x>12
<=>5x-3>12
<=>5x>15
<=>x>3
11,  14x+13<20-7x
<=>14x+13+7x<20
<=>21x+13<20
<=>21x<7
<=>x<\(\dfrac{1}{3}\)

ĐỂ (x+1)(x+3)< 0 khi x+1>0, x+3< 0 hoặc x+1<0,x+3> 0

x>-1,x>-3 => x>-1

hoặc x<-1,x<-3 => x<-3

vậy với x>-1 hoặc x<-3 thi (x+1)(x+3) <0

Vì tích trên < 0 => x+1 và x+3 trái dấu.mà x+3-(x+1)=2=>x+3>x+1=>x+3 mang dấu + và x+1 ngược lại=>x+3>0 và x+1 cũng ngược lại

=>nếu x+3>0=>x>3(1)

x+1<0=>x<1(2)

Từu 1 và 2 => 3<x<1

Ủa, vô lí, hì vậy x ko có gt nhé

Nhưng đây là toán nâng cao lớp 6 đó bn ơi

a: \(\Leftrightarrow15\left(x-1\right)-2\left(7x+3\right)\le10\left(2x+1\right)+6\left(3-2x\right)\)

\(\Leftrightarrow15x-15-14x-6\le20x+10+18-12x\)

=>x-21<=8x+28

=>-7x<=49

hay x>=-7

b: \(\Leftrightarrow20\left(2x+1\right)-15\left(2x^2+3\right)< 10x\left(5-3x\right)-12\left(4x+1\right)\)

\(\Leftrightarrow40x+20-30x^2-45< 50x-30x^2-48x-12\)

=>40x-25<2x-12

=>38x<13

hay x<13/38

\(a,\dfrac{x-1}{2}-\dfrac{7x+3}{15}\le\dfrac{2x+1}{3}+\dfrac{3-2x}{5}\\ \Leftrightarrow\dfrac{15\left(x-1\right)}{30}-\dfrac{2\left(7x+3\right)}{30}\le\dfrac{10\left(2x+1\right)}{30}+\dfrac{6\left(3-2x\right)}{30}\\ \Leftrightarrow15x-15-14x-6\le20x+10+18-12x\\ \Leftrightarrow x-21\le8x+28\\ \Leftrightarrow7x+49\ge0\\ \Leftrightarrow x\ge-7\)

\(b,\dfrac{2x+1}{-3}-\dfrac{2x^2+3}{-4}>\dfrac{x\left(5-3x\right)}{-6}-\dfrac{4x+1}{-5}\\ \Leftrightarrow\dfrac{20\left(2x+1\right)}{-60}-\dfrac{15\left(2x^2+3\right)}{-60}>\dfrac{10x\left(5-3x\right)}{-60}-\dfrac{12\left(4x+1\right)}{-60}\\ \Leftrightarrow40x+20-30x^2-45>50x-30x^2-48x-12\\ \Leftrightarrow38x-13>0\\ \Leftrightarrow x>\dfrac{13}{38}\)

\(\sqrt{x-2x^2+1}>1-x\)

TH1: \(1-x\ge0\Rightarrow x\le1\)

\(\sqrt{x-2x^2+1}>1-x\\ \Leftrightarrow x-2x^2+1>x^2-2x+1\\ \Leftrightarrow-2x^2>-2x\\ \Leftrightarrow-2x^2+2x>0\\ \Leftrightarrow-2x\left(x-1\right)>0\\ \Leftrightarrow x\left(x-1\right)< 0\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x\in\left(0;1\right)\end{matrix}\right.\)

TH2: \(1-x< 0\Leftrightarrow x>1\)

Tương tự ........