
Câu c thôi
Giúp mình câu c với ạ, chỉ cần câu c thôi ạ!

Vì \(\widehat{MIA}=90^0\left(\text{góc nt chắn nửa đường tròn}\right)\) nên \(MI\perp IA\)
Xét \(\Delta MBP\) có \(\left\{{}\begin{matrix}PK\perp MB\left(PK\perp MN\right)\\MI\perp PB\left(MI\perp IA\right)\\\left\{H\right\}=PK\cap MI\end{matrix}\right.\) nên H là trực tâm
Do đó \(HB\perp PM\)
Mà \(AM\perp PM\Rightarrow HB\text{//}AM\)
Vì \(HB\text{//}OA\Rightarrow\dfrac{PB}{PA}=\dfrac{HB}{OA}\)
Ta có \(\sin MPB=\sin MPA=\dfrac{MA}{PA}=\dfrac{2OA}{PA}\)
\(\Rightarrow\dfrac{1}{2}BP\cdot\sin MPB=\dfrac{PB\cdot\dfrac{2OA}{PA}}{2}=\dfrac{PB\cdot2OA}{2PA}=\dfrac{PB}{PA}\cdot OA=\dfrac{HB}{OA}\cdot OA=HB\left(đpcm\right)\)
Câu c thôi

Giải giúp câu câu c thôi ạ. Xin cảm ơn
c) ta có EF là dg tb tg ABC(cmt)
=> EF//BC <=> ED//BC( D thuộc EF) (1)
Ta lại có AECD là hbh ( cmt)
=> AE//CD <=> EB//CD( E thuộc AB) (2)
Từ (1) và (2) => EBCD là hbh( dh1 )
=> EC giao BD tại trung điểm mỗi dg
<=> N td BD; G td EC hay EG=GC
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔBAC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)
hay EF=3,6(cm)
b: Xét tứ giác ADCE có
F là trung điểm của đường chéo AC
F là trung điểm của đường chéo ED
Do đó: ADCE là hình bình hành
Suy ra: AE=CD
mà AE=BD
nên CD=BD

câu c thôi ạ
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc HDC+góc HEC=180 độ
=>HDCE nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
góc FCB=góc BAD
=>góc FEB=góc DEB
=>EB là phân giác của góc FED

câu c thôi nhé
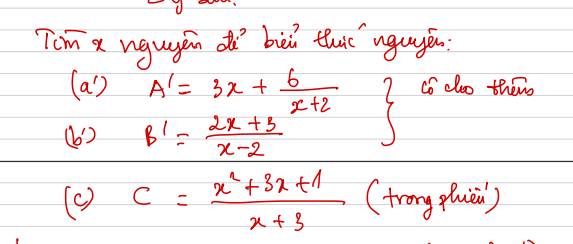
Câu c thôi aa
Lời giải:
$C=\frac{x^2+3x+1}{x+3}=\frac{x(x+3)+1}{x+3}=x+\frac{1}{x+3}$
Với $x$ nguyên, để $C$ nguyên thì $\frac{1}{x+3}$ nguyên.
Với $x$ nguyên, để $\frac{1}{x+3}$ nguyên thì $x+3$ là ước của 1.
$\Rightarrow x+3\in \left\{1; -1\right\}$
$\Rightarrow x\in \left\{-2; -4\right\}$
Câu d thôi ạ, câu a, b, c làm rồi ạ
Làm câu c thôi ạ