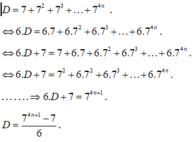A=7+72+73+...+7100

Những câu hỏi liên quan
Tính tổng của A = 7 + 71 + 72 + 73 + .... + 7100
\(A=7+7+7^2+...+7^{100}\)
\(7A=7^2+7^2+7^3+...+7^{101}\)
\(A=14+7^2+7^{101}\)
Đúng 0
Bình luận (0)
Em xem thử lại đề bài nhé
Đúng 0
Bình luận (0)
1)E = 5 + 52 + 53+ ... + 520
CMR E : 7
2) F = 7 + 72+ 73 + 74 + ... + 7100
CMR F : 8
F = 7 + 72 + 73 + 74 + ..... + 7100
F= 7+(1+7)+73+(1+7)+...+799+(1+7)
F = 7x8+73x8+...+799x8
F= 8x(7+73+...+799)
mà 8 chia hết 8 => 8(7+73+...+799) chia hết 8
Vậy F chia hết cho 8
Đúng 3
Bình luận (0)
2)
\(F=7+7^2+7^3+7^4+...+7^{100}\\ F=7\cdot\left(1+7\right)+7^3\cdot\left(1+7\right)+.....+7^{99}\cdot\left(1+7\right)\\F=7\cdot8+7^3\cdot8+.....+7^{99}\cdot8\\ F=8\cdot\left(7+7^3+....+7^{99}\right)\\ =>F⋮8\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Mn giải cho e ặ !
M = 7 + 72 + 73 + 74 + ..... + 7100
M chia hết cho 8
\gấp ặ/
M = 7 + 72 + 73 + 74 + ..... + 7100
M = 7+(1+7)+73+(1+7)+...+799+(1+7)
M = 7x8+73x8+...+799x8
M = 8x(7+73+...+799)
mà 8 chia hết 8 => 8(7+73+...+799) chia hết 8
Vậy M chia hết cho 8
Đúng 1
Bình luận (0)
A=7+72+...+7100/7+72+...+799
B=9+92+...+9100/9+92+...+999
So sánh A và B
umm, bn nhân A với 1/7 và nhân B với 1/9, sau đó tính ra và so sánh thôi
Đúng 0
Bình luận (0)
Cho 2a - b 7;
a
≠
-
7
3
;
b
≠
7
2
. Tính giá trị của biểu thức A
5a
−
b
3a
+
7
+
3b
−
2a
2b...
Đọc tiếp
Cho 2a - b = 7; a ≠ - 7 3 ; b ≠ 7 2 . Tính giá trị của biểu thức
A = 5a − b 3a + 7 + 3b − 2a 2b − 7 .
A. 3
B. 4
C. 1
D. 2
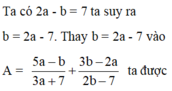
A = 5 a − 2 a − 7 3 a + 7 + 3 2 a − 7 − 2 a 2 2 a − 7 − 7
Đúng 0
Bình luận (0)
Cho A =7 + 72 + 73 + ... + 7119 + 7120. Chứng minh chia hết cho 57
\(A=7+7^2+7^3+...+7^{120}\\ A=\left(7+7^2+7^3\right)+...+\left(7^{118}+7^{119}+7^{120}\right)\\ A=7\times\left(1+7+7^2\right)+...+7^{118}\times\left(1+7+7^2\right)\\ A=7\times57+7^4\times57+...+7^{118}\times57\\ A=57\times\left(7+7^4+...+7^{118}\right)\\ \Rightarrow A⋮57\)
Đúng 4
Bình luận (0)
Câu 3: Cho A = 7 + 72 + 73 + ... + 7119 + 7120. Chứng minh rằng A chia hết cho 57.
\(A=7\left(1+7+7^2\right)+7^4\left(1+7+7^2\right)+...+7^{118}\left(1+7+7^2\right)=7.57+7^4.57+...+7^{118}.57=57\left(7+7^4+...+7^{118}\right)⋮57\)
Đúng 1
Bình luận (0)
Lời giải:
$A=(7+7^2+7^3)+(7^4+7^5+7^6)+....+(7^{118}+7^{119}+7^{120})$
$=7(1+7+7^2)+7^4(1+7+7^2)+...+7^{118}(1+7+7^2)$
$=7.57+7^4.57+...+7^{118}.57$
$=57(7+7^4+...+7^{118})\vdots 57$
Ta có đpcm.
Đúng 3
Bình luận (1)
Cho A = 7 + 72 + 73 + ... + 7119 + 7120. Chứng minh rằng A chia hết cho 57.
giúp mình với
Tính tổng
S= 7+ 72+73+.....+720
\(S=7+7^2+7^3+...7^{20}\)
Ta có: \(7S=7.\left(7+7^2+7^3+...+7^{20}\right)\)
\(7S=7^2+7^3+7^4+...+7^{21}\)
\(7S-S=\left(7^2+7^3+7^4+...+7^{21}\right)-\left(7+7^2+7^3+...+7^{20}\right)\)
\(6S=\left(7^{21}-7\right)\)
\(S=\left(7^{21}-7\right):6\)
Chúc bạn học tốt
Đúng 2
Bình luận (0)
7S=7^2+7^3+...+7^21
=>6S=7^21-7
=>S=(7^21-7)/6
Đúng 0
Bình luận (0)
Tính tổng: D = 7 + 7 2 + 7 3 + … 7 4 n