nHỊ THỨC NEWTON LÀ GÌ

Những câu hỏi liên quan
Nêu một số ví dụ về Nhị Thức Newton
Nhị thức Newton là gì
Tham khảo :
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n ((a+b)n) thành một đa thức có n+1 số hạng.
HT
Công thức
Nhị thức Newton là gì
Tham khảo
Trong toán học, định lý khai triển nhị thức (ngắn gọn là định lý nhị thức) là một định lý toán học về việc khai triển hàm mũ của tổng. Cụ thể, kết quả của định lý này là việc khai triển một nhị thức bậc {\displaystyle n} thành một đa thức có {\displaystyle n+1} số hạng:
{\displaystyle (x+a)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}a^{k}}
với:
{\displaystyle {n \choose k}={\frac {n!}{(n-k)!k!}}}
Gọi là số tổ hợp chập k của n phần tử.
Định lý này đã được độc lập chứng minh bởi hai người đó là:
Nhà toán học và cơ học Isaac Newton tìm ra trong năm 1665.Nhà toán học James Gregory tìm ra trong năm 1670.Công thức đã giới thiệu còn mang tên là Nhị thức Newton.
Đúng 0
Bình luận (0)
Tham khảo
Trong toán học, định lý khai triển nhị thức là một định lý toán học về việc khai triển hàm mũ của tổng. Cụ thể, kết quả của định lý này là việc khai triển một nhị thức bậc n thành một đa thức có {\displaystyle n+1} số hạng: {\displaystyle ^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}a^{k}}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Lý thuyết nhị thức Newton và tam giác Pascal là gì
📘 1. Nhị thức Newton là gì?
Nhị thức Newton là một công thức dùng để khai triển lũy thừa của một tổng dạng \(\left(\right. a + b \left.\right)^{n}\), trong đó \(n\) là số tự nhiên.
✅ Công thức nhị thức Newton:\(\left(\right. a + b \left.\right)^{n} = \sum_{k = 0}^{n} \left(\right. \frac{n}{k} \left.\right) a^{n - k} b^{k}\)
Trong đó:
\(\left(\right. \frac{n}{k} \left.\right)\) là hệ số nhị thức, đọc là "n chọn k", được tính bằng:\(\left(\right. \frac{n}{k} \left.\right) = \frac{n !}{k ! \left(\right. n - k \left.\right) !}\)
\(a , b\) là các biểu thức hoặc số thực.\(n\) là số mũ nguyên không âm (0, 1, 2, ...)🎯 Ví dụ:Khai triển \(\left(\right. a + b \left.\right)^{3}\) bằng nhị thức Newton:
\(\left(\right. a + b \left.\right)^{3} = \left(\right. \frac{3}{0} \left.\right) a^{3} b^{0} + \left(\right. \frac{3}{1} \left.\right) a^{2} b^{1} + \left(\right. \frac{3}{2} \left.\right) a^{1} b^{2} + \left(\right. \frac{3}{3} \left.\right) a^{0} b^{3}\) \(= 1 a^{3} + 3 a^{2} b + 3 a b^{2} + 1 b^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}\)
🟨 2. Tam giác Pascal là gì?Tam giác Pascal là một bảng sắp xếp các hệ số nhị thức \(\left(\right. \frac{n}{k} \left.\right)\) theo hình tam giác. Mỗi số trong tam giác là tổng của hai số phía trên nó.
🔻 Cấu trúc của tam giác Pascal: 1 ← hàng 0 1 1 ← hàng 1 1 2 1 ← hàng 2 1 3 3 1 ← hàng 3 1 4 6 4 1 ← hàng 4 1 5 10 10 5 1 ← hàng 5 ... Mỗi hàng ứng với khai triển của \(\left(\right. a + b \left.\right)^{n}\)Hệ số của \(\left(\right. a + b \left.\right)^{n}\) là các số ở hàng thứ \(n\) của tam giác Pascal.🎯 Ví dụ ứng dụng:Dùng tam giác Pascal để khai triển \(\left(\right. x + y \left.\right)^{4}\):
→ Hàng thứ 4 là: 1 4 6 4 1
\(\left(\right. x + y \left.\right)^{4} = 1 x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + 1 y^{4}\)
✅ Tóm tắt dễ nhớ:Nội dung | Nhị thức Newton | Tam giác Pascal |
|---|---|---|
Khái niệm | Khai triển \(\left(\right. a + b \left.\right)^{n}\)(a+b)n(a + b)^n(a+b)n | Bảng hệ số \(\left(\right. \frac{n}{k} \left.\right)\)(nk)\binom{n}{k}(kn) |
Dạng tổng quát | \(\left(\right. a + b \left.\right)^{n} = \sum_{k = 0}^{n} \left(\right. \frac{n}{k} \left.\right) a^{n - k} b^{k}\)(a+b)n=∑k=0n(nk)an−kbk(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k}b^k(a+b)n=∑k=0n(kn)an−kbk | Các hệ số nhị thức được sắp xếp theo hình tam giác |
Ứng dụng | Giải toán khai triển, tổ hợp, tính nhanh | Tìm hệ số nhị thức nhanh chóng, ứng dụng trong nhị thức Newton xin 1 tick |
Đúng 0
Bình luận (0)
@Nguyễn Tuấn Vũ mik đang học đến phần đó bạn nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phân tích đa thức thành nhân tử: x8 - 1
Có cách nào khác cách nhị thức Newton gì đó không ạ?
\(x^8-1=\left(x^2-1\right)\left(x^4+x^2+1\right)\)
CÂU SAU THÌ MK KO BIẾT
Đúng 0
Bình luận (0)
Trong khai triển nhị thức Newton
0
,
7
−
0
,
3
5
, số hạng thứ tư là A. 0,0567 B. 0,3087 C. -0,1323 D. -0,7203
Đọc tiếp
Trong khai triển nhị thức Newton 0 , 7 − 0 , 3 5 , số hạng thứ tư là
A. 0,0567
B. 0,3087
C. -0,1323
D. -0,7203
Hệ số của số hạng chứa
x
7
trong khai triển nhị thức Newton
x
−
1
x
2
10
là A.
C
10
2
B.
C
10
7
C....
Đọc tiếp
Hệ số của số hạng chứa x 7 trong khai triển nhị thức Newton x − 1 x 2 10 là
A. C 10 2
B. C 10 7
C. - 10
D. 10
Đáp án C
Ta có khai triển nhị thức Newton
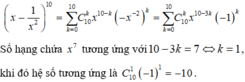
Đúng 0
Bình luận (0)
Hệ số của số hạng chứa
x
7
trong khai triển nhị thức Newton
x
-
1
x
2
10
là A. 10 B.
C
10
2
C.
C
10
7
D. -10
Đọc tiếp
Hệ số của số hạng chứa x 7 trong khai triển nhị thức Newton x - 1 x 2 10 là
A. 10
B. C 10 2
C. C 10 7
D. -10
Đáp án D
Ta có khai triển nhị thức Newton
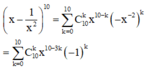
Số hạng chứa
x
7
tương ứng với ![]() khi đó hệ số tương ứng là
khi đó hệ số tương ứng là
![]()
Đúng 0
Bình luận (0)
Hệ số của số hạng chứa
x
7
trong khai triển nhị thức Newton
x
-
1
x
2
10
là
Đọc tiếp
Hệ số của số hạng chứa x 7 trong khai triển nhị thức Newton x - 1 x 2 10 là
![]()
![]()
![]()
![]()
Nêu ví dụ về nhị thức Newton
Tham khảo :
chrome-untrusted://new-tab-page/custom_background_image?url=https%3A%2F%2Flh5.googleusercontent.com%2Fproxy%2FtjJRG8ELyrHCJQ18ThdF1ybYJ9CP1q6jDyCAECruLxqefc2gvH9YYUjKItQyvmWClmOoC3XivqciC7PbY2-
1NtWxLE7fNsJFqYflxTi2EyE%3Dw3840-h2160-p-k-no-nd-mv
Đúng 0
Bình luận (0)





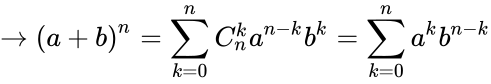


 thành một đa thức có {\displaystyle n+1}
thành một đa thức có {\displaystyle n+1} số hạng:
số hạng:

















