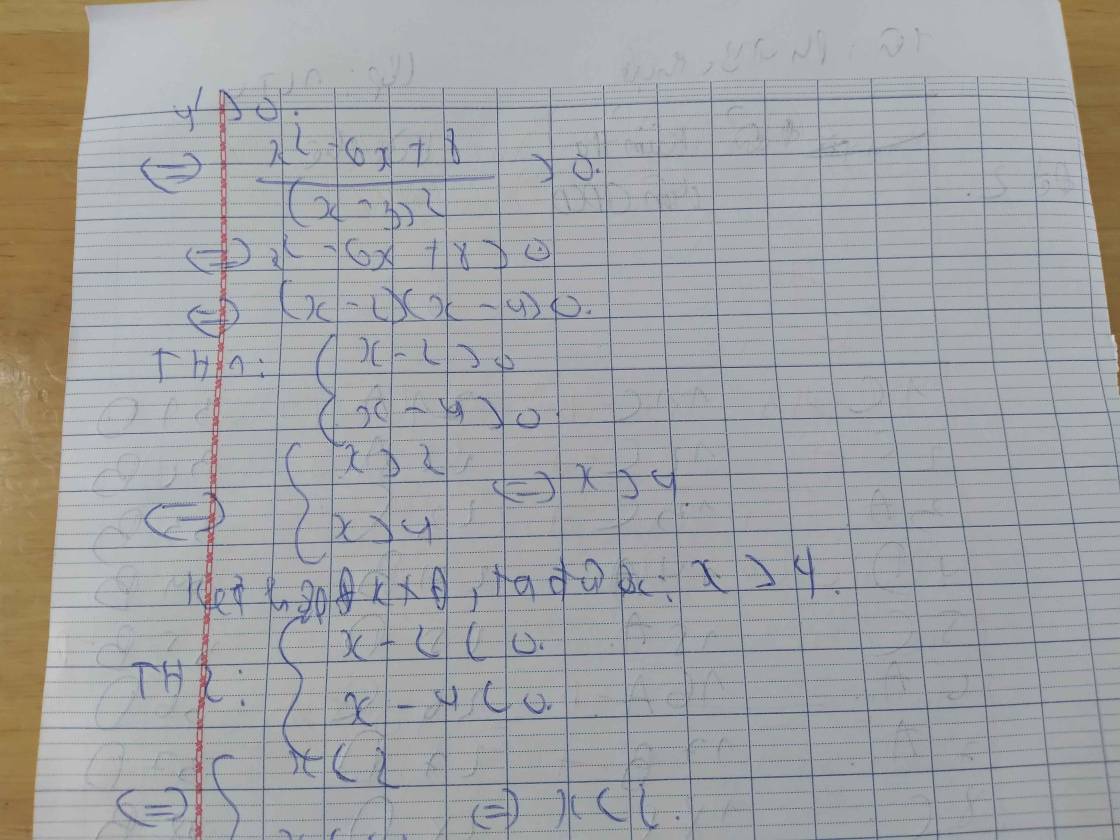y = \(\sqrt{x^2-2x+5}\) - \(\sqrt[]{x^2+6x+10}\)

Những câu hỏi liên quan
Giải các phương trình dưới đây
1, \(\sqrt{9x^2-6x+2}+\sqrt{45x^2-30x+9}=\sqrt{6x-9x^2+8}\)
2,\(\sqrt{2x^2-4x+3}+\sqrt{3x^2-6x+7}=2-x^2+2x\)
3, \(\sqrt{6y-y^2-5}-\sqrt{x^2-6x+10}=1\) (x=3 ; y=3)
giải phương trình
a)\(\sqrt{6y-y^2-5}-\sqrt{x^2-6x+10}=1\)
b)\(\sqrt{2x^2-4x+3}+\sqrt{3x^2-6x+7}=2-x^2+2x\)
b) ĐK: \(1-\sqrt{3}< x< 1+\sqrt{3}\).Đặt:
\(\sqrt{2x^2-4x+3}-1+\sqrt{3x^2-6x+7}-2+x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2\left[\frac{2}{\sqrt{2x^2-4x+3}+1}+\frac{3}{\sqrt{3x^2-6x+7}+2}+1\right]=0\)
Cái ngoặc to vô nghiệm.Do đó x = 1(TM)
Vậy...
P.s: Nãy giờ em đi đánh giá lung tùng nào là "truy ngược dấu liên hợp" mất cả tiếng đồng hồ không ra và cảm thấy uổng phí quá:( Bài này nếu sai thì em chịu luôn
Đúng 0
Bình luận (0)
Èo, bỏ chữ Đặt giúp em(nãy tính làm cách đặt ẩn phụ như không ra mà quên xóa đi) >_<
Đúng 0
Bình luận (0)
a.\(DK:x\in R,1\le y\le5\)
.\(\Leftrightarrow\sqrt{4-\left(3-y\right)^2}-\sqrt{\left(x-3\right)^2+1}=1\)
Ta co:\(\sqrt{4-\left(3-y\right)^2}\le2\left(1\right)\)
\(\sqrt{\left(x-3\right)^2+1}\ge1\left(1\right)\)
Tru ve voi ve cua (1) va (2) ta duoc:
\(\sqrt{4-\left(3-y\right)^2}-\sqrt{\left(x-3\right)^2+1}\le1\)
Dau '=' xay ra khi \(x=y=3\)
Vay nghiem cua PT la \(x=y=3\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm khoảng đồng biến nghịch biến
a) \(y=\sqrt{x^2+2x+3}\)
b) \(y=\sqrt{4-x^2}\)
c) \(y=\dfrac{x^2-6x+10}{x-3}\)
d) \(y=\sqrt{-x+2x}\)
e) \(y=\sqrt{4+5x^2}\)
\(\hept{\begin{cases}x^3-y^2-6x^2+13x-y=10\\\sqrt{2x+y+5}-\sqrt{3-x-y}=\left(2x-5\right)y+2\end{cases}}\)
giải pt sau
\(\sqrt{x^2+2x+5}=-x^2-2x+1\)
\(\sqrt{x^2-6x+10}+\sqrt{4x^2-24x+45}=-x^2+6x-5\)
\(\sqrt{x^2+2x+5}=-x^2-2x+1\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2+4}=-\left(x+1\right)^2+2\)
Ta thấy :
\(-\left(x+1\right)^2+2\le2\) Với \(\forall x\in R\)
\(\sqrt{\left(x+1\right)^2+4}\ge2\) Với \(\forall x\in R\)
\(\Rightarrow\sqrt{\left(x+1\right)^2+4}=-\left(x+1\right)^2+2\) Khi x + 1 = 0 \(\Leftrightarrow\) x = -1
Vậy Phương trình có nghiệm x = -1 .
Đúng 0
Bình luận (0)
\(\sqrt{x^2-6x+10}+\sqrt{4x^2-24x+45}=-x^2+6x-5\)
Ta thấy :
\(\sqrt{x^2-6x+10}=\sqrt{\left(x-3\right)^2+1}\) \(\ge1\) Với \(\forall x\in R\)
\(\sqrt{4x^2-24x+45}=\sqrt{4\left(x-3\right)^2+9}\ge3\) Với \(\forall x\in R\)
\(-x^2+6x-5=-\left(x-3\right)^2+4\le4\) Với \(\forall x\in R\)
\(\Rightarrow VT\ge4\) ; \(VP\le4\)
\(\Rightarrow VT=VP=4\)
Dấu "=" xảy ra khi x - 3 = 0 \(\Leftrightarrow\) x = 3
Vậy phương trình có nghiệm x = 3 .
Đúng 0
Bình luận (0)
\(a.\sqrt{x^2+2x+5}=-x^2-2x+1\)
Ta có : \(VT=\sqrt{x^2+2x+5}=\sqrt{\left(x+1\right)^2+4}\) ≥ \(2\)
\(VP=-x^2-2x+1=-\left(x^2+2x+1\right)+2=-\left(x+1\right)^2+2\) ≤ \(2\)
Để : \(\sqrt{\left(x+1\right)^2+4}=-\left(x+1\right)^2+2\)
⇔ \(x=-1\)
KL...........
\(b.\sqrt{x^2-6x+10}+\sqrt{4x^2-24x+45}=-x^2+6x-5\)
Ta có : \(\sqrt{x^2-6x+10}=\sqrt{\left(x-3\right)^2+1}\text{≥}1\left(1\right)\)
\(\sqrt{4x^2-24x+45}=\sqrt{4\left(x-3\right)^2+9}\text{≥}3\left(2\right)\)
\(-x^2+6x-5=-\left(x^2-6x+9\right)+4=-\left(x-3\right)^2+4\text{≥}4\left(3\right)\)
Từ ( 1 ; 2 ) , ta có :
\(\sqrt{\left(x-3\right)^2+1}+\sqrt{4\left(x-3\right)^2+9}\text{≥}4\left(4\right)\)
Từ ( 3 ; 4 ) để : \(\sqrt{\left(x-3\right)^2+1}+\sqrt{4\left(x-3\right)^2+9}=-\left(x-3\right)^2+4\)
⇔ \(x=3\)
KL..........
Đúng 0
Bình luận (0)
Giải hệ phương trình: \(\begin{cases}y^3-3y^2-6x+2=\frac{\sqrt{y^3+6x+10}-\sqrt{2y^3-3y^2}}{x^2+2x+2016}\\\sqrt{2x^2-xy+x}=3y-2x-3\end{cases}\)
Giải hệ phương trình : \(\left\{{}\begin{matrix}x^3-y^3-6x^2+13x-y=10\\\sqrt{2x+y+5}-\sqrt{3-x-y}=\left(2x-5\right)y+2\end{matrix}\right.\)
giải pt:
a,\(\left(13-4x\right)\sqrt{2x-3}+\left(4x-3\right)\sqrt{5-2x}=2+8\sqrt{-4x^2+16x-15}\)
b,\(\left(9x-2\right)\sqrt{3x-1}+\left(10-9x\right)\sqrt{3-3x}-4\sqrt{-9x^2+12x-3}=4\)
c, \(\left(6x-5\right)\sqrt{x+1}-\left(6x+2\right)\sqrt{x-1}+4\sqrt{x^2-1}=4x-3\)
\(\left\{{}\begin{matrix}x^3-6x^2+13x=y^3+y+10\\\sqrt{2x+y+5}-\sqrt{3-x-y}=x^3-3x^2-10y+6\end{matrix}\right.\)
$$\left\{\begin{aligned} &\sqrt{2x+y+5}-\sqrt{3-x-y}=x^3-3x^2-10y+6 &&(1) \\ &x^3-6x^2+13x=y^3+y+10 &&(2)\end{aligned}\right.$$
Lời giải. Điều kiện: $2x+y+5 \ge 0$ và $3-x-y \ge 0.$ Phương trình (2) có thể viết lại thành $$(x^3-6x^2+12x-8)+(x-2)=y^3+y,$$ hay $$(x-2)^3+(x-2)=y^3+y.$$ Phương trình trên có dạng $f(x-2)=f(y)$ với $f(t)=t^3+t.$ Do $f(t)$ là hàm liên tục và tăng nghiêm ngặt trên $\mathbb R$ nên từ đây, ta có $y=x-2.$ Thay vào (1), ta được $$\sqrt{3x+3}-\sqrt{5-2x}=x^3-3x^2-10x+26. \text{ }(3)$$ Lúc này, ta có điều kiện tương ứng cho $x$ là $-1 \le x \le \frac{5}{2}.$ Với điều kiện này, phương trình (3) tương đương với $$ \left(\sqrt{3x+3}-3\right)+\left(1-\sqrt{5-2x}\right)-(x^3-3x^2-10x+24)=0,$$ hay $$\frac{3(x-2)}{\sqrt{3x+3}+3}+\frac{2(x-2)}{\sqrt{5-2x}+1}+(x-2)(4-x)(x+3)=0.$$ Đưa $x-2$ ra làm nhân tử chung, ta được $$(x-2)\left[\frac{3}{\sqrt{3x+3}+3}+\frac{2}{\sqrt{5-2x}+1}+(4-x)(x+3)\right]=0.$$ Do $-1 \le x\le \frac{5}{2}$ nên dễ thấy $$\frac{3}{\sqrt{3x+3}+3}+\frac{2}{\sqrt{5-2x}+1}+(4-x)(x+3)>0.$$ Từ đây, ta suy ra ngay $x=2$ và $y=x-2=0.$ Vậy hệ có nghiệm duy nhất $(x,\,y)=(2,\,0).$