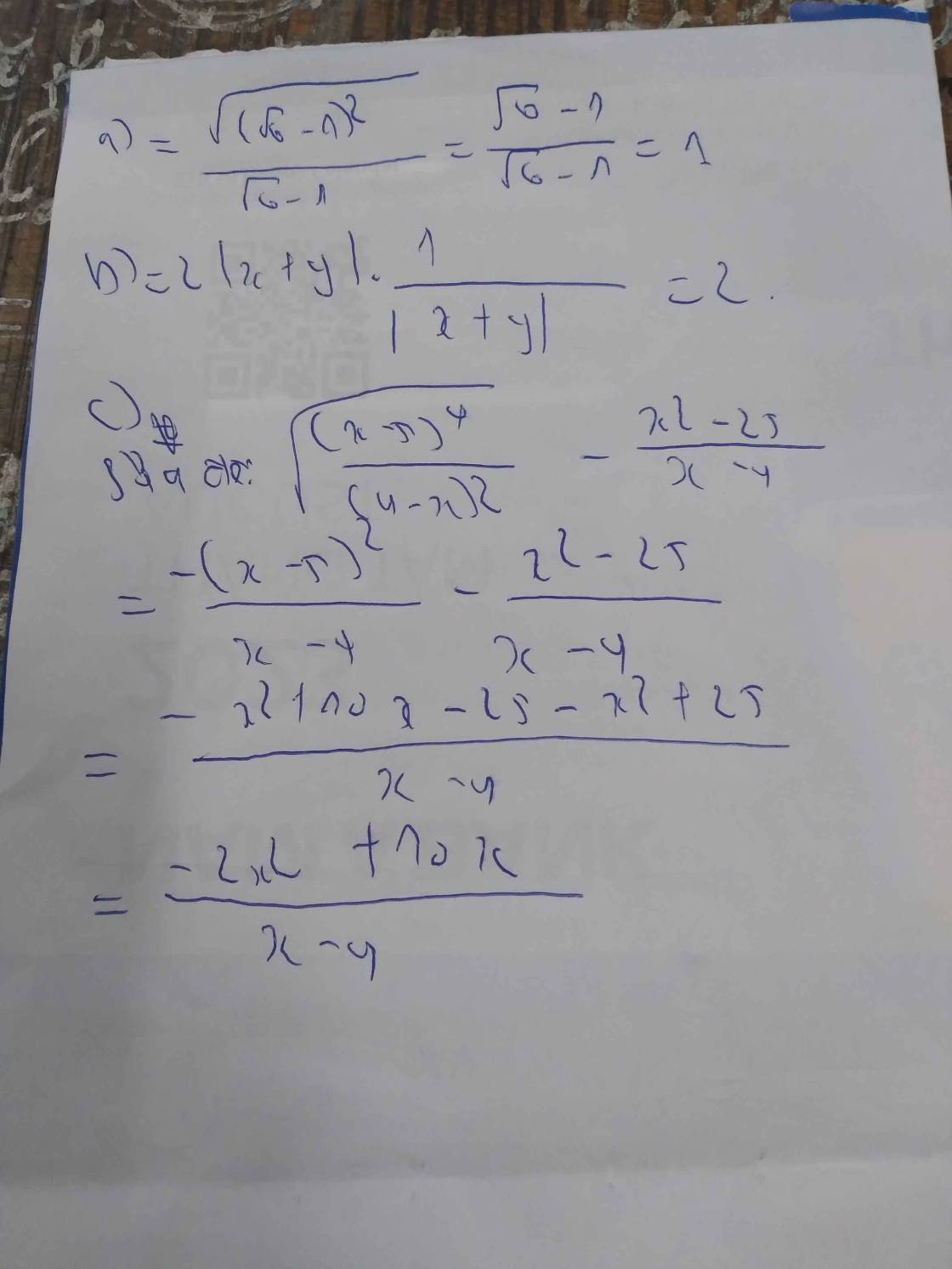\(log_{\sqrt{3}}\left(2x+y\right)-log_{\sqrt{3}}\left(4x^2+y^2+2xy+2\right)=\left(4x^2+y^2+2xy+2\right)-3\left(2x+y\right)-2\)

\(\Leftrightarrow log_{\sqrt{3}}\left(2x+y\right)+2+3\left(2x+y\right)=log_{\sqrt{3}}\left(4x^2+y^2+2xy+2\right)+\left(4x^2+y^2+2xy+2\right)\)

\(\Leftrightarrow log_{\sqrt{3}}\left(6x+3y\right)+\left(6x+3y\right)=log_{\sqrt{3}}\left(4x^2+y^2+2xy+2\right)+\left(4x^2+y^2+2xy+2\right)\)

Xét hàm \(f\left(t\right)=log_{\sqrt{3}}t+t\) với \(t>0\)

\(f'\left(t\right)=\dfrac{1}{t.ln\sqrt{3}}+1>0\Rightarrow f\left(t\right)\) đồng biến

\(\Rightarrow6x+3y=4x^2+y^2+2xy+2\)

\(\Leftrightarrow4x+y=\left(x+y-1\right)^2+1+3\left(x^2+1\right)-3\ge2\left(x+y-1\right)+6x-3\)

\(\Leftrightarrow4x+y\ge2\left(4x+y\right)-5\)

\(\Leftrightarrow4x+y\le5\)

\(\Rightarrow P=\dfrac{2x+y+6+\left(4x+y-5\right)}{2x+y+6}=1+\dfrac{4x+y-5}{2x+y+6}\le1\)

\(P_{max}=1\) khi \(x=y=1\)

Coi như tất cả các biểu thức cần tính đạo hàm đều xác định.

1.

\(y'=2sin\sqrt{4x+3}.\left(sin\sqrt{4x+3}\right)'=2sin\sqrt{4x+3}.cos\sqrt{4x+3}.\left(\sqrt{4x+3}\right)'\)

\(=sin\left(2\sqrt{4x+3}\right).\dfrac{4}{2\sqrt{4x+3}}=\dfrac{2sin\left(2\sqrt{4x+3}\right)}{\sqrt{4x+3}}\)

2.

\(y'=3x^3+\dfrac{17}{x\sqrt{x}}\)

3.

\(y'=\dfrac{1}{2\sqrt{\dfrac{sin4x}{cos\left(x^2+2\right)}}}.\left(\dfrac{sin4x}{cos\left(x^2+2\right)}\right)'\)

\(=\dfrac{1}{2\sqrt{\dfrac{sin4x}{cos\left(x^2+2\right)}}}.\dfrac{4cos4x.cos\left(x^2+2\right)+2x.sin4x.sin\left(x^2+2\right)}{cos^2\left(x^2+2\right)}\)

4.

\(y'=-\dfrac{\left(\sqrt{sin^2\left(6-x\right)+4x}\right)'}{sin^2\left(6-x\right)+4x}=-\dfrac{\left[sin^2\left(6-x\right)+4x\right]'}{2\sqrt{\left[sin^2\left(6-x\right)+4x\right]^3}}\)

\(=-\dfrac{2sin\left(6-x\right).\left[sin\left(6-x\right)\right]'+4}{2\sqrt{\left[sin^2\left(6-x\right)+4x\right]^3}}=-\dfrac{-2sin\left(6-x\right).cos\left(6-x\right)+4}{2\sqrt{\left[sin^2\left(6-x\right)+4x\right]^3}}\)

\(=\dfrac{sin\left(12-2x\right)-4}{2\sqrt{\left[sin^2\left(6-x\right)+4x\right]^3}}\)

5.

\(y'=sin^2\left(\dfrac{2x-1}{4-x}\right)+2x.sin\left(\dfrac{2x-1}{4-x}\right).\left[sin\left(\dfrac{2x-1}{4-x}\right)\right]'\)

\(=sin^2\left(\dfrac{2x-1}{4-x}\right)+2x.sin\left(\dfrac{2x-1}{4-x}\right).cos\left(\dfrac{2x-1}{4-x}\right).\left(\dfrac{2x-1}{4-x}\right)'\)

\(=sin^2\left(\dfrac{2x-1}{4-x}\right)+x.sin\left(\dfrac{4x-2}{4-x}\right).\dfrac{7}{\left(4-x\right)^2}\)

8.

\(y=tan^33x-\left(sin2x+cos3x\right)^5\)

\(\Rightarrow y'=3tan^23x.\left(tan3x\right)'-5\left(sin2x+cos3x\right)^4.\left(sin2x+cos3x\right)'\)

\(=\dfrac{9.tan^23x}{cos^23x}-5\left(sin2x+cos3x\right)^4.\left(2cos2x-3sin3x\right)\)

9.

\(y'=6cot^55x.\left(cot5x\right)'-4cos^33x.\left(cos3x\right)'+3cos3x\)

\(=-\dfrac{30.cot^55x}{sin^25x}+12cos^33x.sin3x+3cos3x\)

a)

Ta có: $2x^2+2y^2=5xy \Leftrightarrow 2\frac{x}{y}+\frac{y}{x}=5$

Đặt $t=\frac{x}{y}$, ta có $2t+\frac{1}{t}=5 \Rightarrow 2t^2-5t+1=0$

Giải phương trình trên ta được $t_1=\frac{1}{2}$ và $t_2=1$. Vì $0<x<y$ nên $t>0$, do đó $t=\frac{x}{y}=\frac{1}{2}$.

Từ đó suy ra $x=\frac{y}{2}$ và thay vào biểu thức $E$ ta được:

$E=\frac{x^2+y^2}{x^2-y^2}=\frac{\frac{y^2}{4}+y^2}{\frac{y^2}{4}-y^2}=-\frac{5}{3}$

Vậy kết quả là $E=-\frac{5}{3}$.

đặt $a=\frac{1}{\sqrt[3]{3-2\sqrt{2}}}$, $b=\sqrt[3]{3-2\sqrt{2}}}$

Khi đó:
$$(a+b)^3=a^3+b^3+3ab(a+b)$$
$$a^3+b^3=\left(\frac{1}{\sqrt[3]{3-2\sqrt{2}}}\right)^3+\left(\sqrt[3]{3-2\sqrt{2}}\right)^3= \frac{1}{3-2\sqrt{2}}+(3-2\sqrt{2})=4$$
$$ab=\frac{1}{\sqrt[3]{3-2\sqrt{2}}}\cdot\sqrt[3]{3-2\sqrt{2}}=\sqrt[3]{(3-2\sqrt{2})(3+2\sqrt{2})}=\sqrt[3]{1}=1$$
Do đó, ta có:
$$(a+b)^3=4+3ab(a+b)=4+3(a+b)$$
Vậy $2x^3=2(a+b)^3=8+6(a+b)$ và $6x=6(a+b)$.
Thay vào biểu thức $P$, ta được:
$$P=\left(2x^3-6x+2008\right)^{2021}=\left(8+6(a+b)-6(a+b)+2008\right)^{2021}=2016^{2021}$$
Vậy kết quả là $P=2016^{2021}$.

\(5x^2+2xy+2y^2-\left(4x^2+4xy+y^2\right)=\left(x-y\right)^2\ge0\\ \Leftrightarrow5x^2+2xy+2y^2\ge4x^2+4xy+y^2=\left(2x+y\right)^2\)

\(\Leftrightarrow P\le\dfrac{1}{2x+y}+\dfrac{1}{2y+z}+\dfrac{1}{2z+x}=\dfrac{1}{9}\left(\dfrac{9}{x+x+y}+\dfrac{9}{y+y+z}+\dfrac{9}{z+z+x}\right)\\ \Leftrightarrow P\le\dfrac{1}{9}\left(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{y}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{z}+\dfrac{1}{z}+\dfrac{1}{x}\right)\\ \Leftrightarrow P\le\dfrac{1}{9}\left(\dfrac{3}{x}+\dfrac{3}{y}+\dfrac{3}{z}\right)=\dfrac{1}{3}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=1\)

Dấu \("="\Leftrightarrow x=y=z=1\)

\(\sqrt{5x^2+2xy+2y^2}=\sqrt{4x^2+2xy+y^2+x^2+y^2}\ge\sqrt{4x^2+2xy+y^2+2xy}=2x+y\)

\(\Rightarrow\dfrac{1}{\sqrt{5x^2+2xy+2y^2}}\le\dfrac{1}{2x+y}=\dfrac{1}{x+x+y}\le\dfrac{1}{9}\left(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{y}\right)=\dfrac{1}{9}\left(\dfrac{2}{x}+\dfrac{1}{y}\right)\)

Tương tự:

\(\dfrac{1}{\sqrt{5y^2+2yz+2z^2}}\le\dfrac{1}{9}\left(\dfrac{2}{y}+\dfrac{1}{z}\right)\) ; \(\dfrac{1}{\sqrt{5z^2+2zx+2x^2}}\le\dfrac{1}{9}\left(\dfrac{2}{z}+\dfrac{1}{x}\right)\)

Cộng vế:

\(P\le\dfrac{1}{9}\left(\dfrac{3}{x}+\dfrac{3}{y}+\dfrac{3}{z}\right)=1\)

\(P_{max}=1\) khi \(x=y=z=1\)

a/ \(y'=\dfrac{\left(x^3+2\sqrt{x-1}\right)'\left(x-1\right)-\left(x-1\right)'\left(x^3+2\sqrt{x-1}\right)}{\left(x-1\right)^2}\)

\(y'=\dfrac{\left(2x^2+\dfrac{1}{\sqrt{x-1}}\right)\left(x-1\right)-x^3-2\sqrt{x-1}}{\left(x-1\right)^2}=\dfrac{x^3-2x^2-\sqrt{x-1}}{\left(x-1\right)^2}\)

b/ \(y'=\dfrac{\left(4x^3+2x-3\right)'\left(\sqrt{x^2+2}\right)-\left(\sqrt{x^2+2}\right)'\left(4x^3+2x-3\right)}{x^2+2}\)

\(y'=\dfrac{\left(12x^2+2\right)\sqrt{x^2+2}-\dfrac{x}{\sqrt{x^2+2}}\left(4x^3+2x-3\right)}{x^2+2}\) (ban tu rut gon nhe)

c/ \(y'=\dfrac{\left(x^3+x+1\right)'\left(x^3+x+1\right)}{\left|x^3+x+1\right|}=\dfrac{\left(3x^2+1\right)\left(x^3+x+1\right)}{\left|x^3+x+1\right|}\) 

d/ \(y'=\dfrac{3x^2-24x^3}{2\sqrt{x^3-6x^4+7}}\)

e/ \(y'=\dfrac{\left(x^5+1\right)'\left(2-\sqrt{x^2+3}\right)-\left(x^5+1\right)\left(2-\sqrt{x^2+3}\right)'}{\left(2-\sqrt{x^2+3}\right)^2}\)

\(y'=\dfrac{5x^4\left(2-\sqrt{x^2+3}\right)+\left(x^5+1\right)\dfrac{x}{\sqrt{x^2+3}}}{\left(2-\sqrt{x^2+3}\right)^2}\)