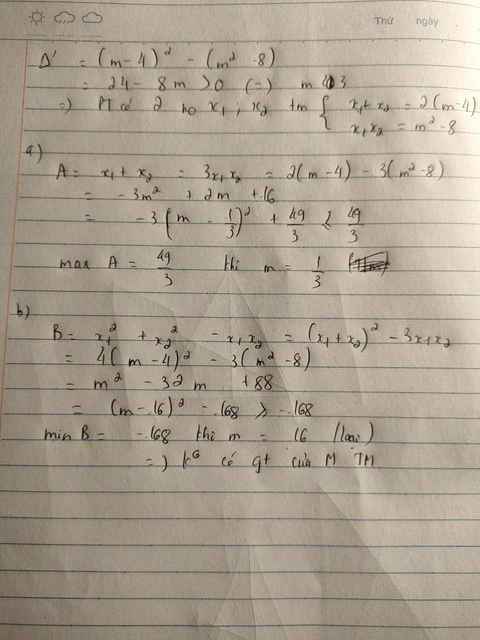đưa cả bài ms làm đc chứ

\(\Delta'=\left(-2\right)^2-3.\left(-8\right)=4+24=28>0.\)

\(\Rightarrow\) Pt có 2 nghiệm phân biệt \(x_1;x_2.\)

\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{2+2\sqrt{7}}{3}.\\x_2=\dfrac{2-2\sqrt{7}}{3}.\end{matrix}\right.\)

\(\Delta'=\left(-\sqrt{5}\right)^2-1.2=5-2=3>0\)

Suy ra pt luôn có 2 nghiệm phân biệt

Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2\sqrt{5}\\x_1x_2=2\end{matrix}\right.\)

\(E=\dfrac{x^2_1+x_1x_2+x^2_2}{x^2_1+x^2_2}\\ =\dfrac{\left(x_1+x_2\right)^2-x_1x_2}{\left(x_1+x_2\right)^2-2x_1x_2}\\ =\dfrac{\left(2\sqrt{5}\right)^2-2}{\left(2\sqrt{5}\right)^2-2.2}\\ =\dfrac{20-2}{20-4}\\ =\dfrac{18}{16}\\ =\dfrac{9}{8}\)
 

\(E=\dfrac{\left(x_1+x_2\right)^2-x_1x_2}{\left(x_1+x_2\right)^2-2x_1x_2}=\dfrac{4.5-2}{4.5-2.2}=\dfrac{18}{16}=\dfrac{9}{8}\)

`1)`

$a\big)\Delta=7^2-5.4.1=29>0\to$ PT có 2 nghiệm pb

$b\big)$

Theo Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{7}{5}\\x_1x_2=\dfrac{1}{5}\end{matrix}\right.\)

\(A=\left(x_1-\dfrac{7}{5}\right)x_1+\dfrac{1}{25x_2^2}+x_2^2\\ \Rightarrow A=\left(x_1-x_1-x_2\right)x_1+\left(\dfrac{1}{5}\right)^2\cdot\dfrac{1}{x_2^2}+x_2^2\\ \Rightarrow A=-x_1x_2+\left(x_1x_2\right)^2\cdot\dfrac{1}{x_2^2}+x_2^2\)

\(\Rightarrow A=-x_1x_2+x_1^2+x_2^2\\ \Rightarrow A=\left(x_1+x_2\right)^2-3x_1x_2\\ \Rightarrow A=\left(\dfrac{7}{5}\right)^2-3\cdot\dfrac{1}{5}=\dfrac{34}{25}\)

\(\Delta'=1-\left(m-3\right)=4-m>0\Rightarrow m< 4\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)

\(x_1^2+4x_1x_2+3x_2^2=0\)

\(\Leftrightarrow\left(x_1+x_2\right)\left(x_1+3x_2\right)=0\)

\(\Leftrightarrow2\left(x_1+3x_2\right)=0\)

\(\Leftrightarrow x_1=-3x_2\)

Thế vào \(x_1+x_2=2\Rightarrow-2x_2=2\)

\(\Rightarrow x_2=-1\Rightarrow x_1=3\)

Thế vào \(x_1x_2=m-3\)

\(\Rightarrow m-3=-3\Rightarrow m=0\) (thỏa mãn)

đầu bài có bị sai k bạn

\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\)

Pt có 2 nghiệm khi \(m^2-9\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)

Khi đó theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)

\(A=x_1^2+x_2^2+14x_1x_2=\left(x_1+x_2\right)^2+12x_1x_2\)

\(=4\left(m+1\right)^2+12\left(2m+10\right)\)

\(=4\left(m+4\right)^2+60\ge60\)

Dấu "=" xảy ra khi \(m+4=0\Rightarrow m=-4\) (thỏa mãn)

\(\text{Δ}=\left(-2m\right)^2-4\left(2m-3\right)\)

\(=4m^2-8m+12\)

\(=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\forall m\)

=>Phương trình (1) luôn có hai nghiệm phân biệt

Áp dụng Vi-et, ta được: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-2m\right)}{1}=2m\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)

\(9-x_1^2-x_2^2>=0\)

=>\(9-\left(x_1^2+x_2^2\right)>=0\)

=>\(9-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]>=0\)

=>\(9-\left[\left(2m\right)^2-2\left(2m-3\right)\right]>=0\)

=>\(9-4m^2+4m-6>=0\)

=>\(-4m^2+4m+3>=0\)

=>\(4m^2-4m-3< =0\)

=>\(4m^2-6m+2m-3< =0\)

=>(2m-3)(2m+1)<=0

=>\(-\dfrac{1}{2}< =m< =\dfrac{3}{2}\)

mà m là số nguyên nhỏ nhất

nên m=0

\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)

Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)

Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)

\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)

A_min=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)

\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)

B_min=-168\(\Leftrightarrow\)m=-16

a: \(x_1+x_2=-\dfrac{b}{a}=2\sqrt{3};x_1\cdot x_2=\dfrac{c}{a}=1\)

Đặt \(A=x_1-x_2\)

=>\(A^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)

\(=\left(2\sqrt{3}\right)^2-4\cdot1=12-4=8\)

=>\(\left[{}\begin{matrix}x_1-x_2=2\sqrt{2}\\x_1-x_2=-2\sqrt{2}\end{matrix}\right.\)

b: \(\dfrac{3x_1^2+5x_1x_2+3x_2^2}{4x_1^3\cdot x_2+4x_1\cdot x_2^3}\)

\(=\dfrac{3\left(x_1^2+x_2^2\right)+5x_1x_2}{4x_1x_2\left(x_1^2+x_2^2\right)}\)

\(=\dfrac{3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+5x_1x_2}{4x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}\)

\(=\dfrac{3\left(x_1+x_2\right)^2-x_1x_2}{4x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}\)

\(=\dfrac{3\cdot12-1}{4\cdot1\cdot\left[12-2\cdot1\right]}=\dfrac{35}{4\cdot10}=\dfrac{7}{8}\)