\(y=\left(2-m\right)x+m-1\)

Có: \(\left\{{}\begin{matrix}a=2-m\\b=m-1\end{matrix}\right.\) (ĐK: \(m\ne2\))

a) Để đồ thị (1) đi qua góc tọa độ thì: \(b=0\)

\(\Rightarrow m-1=0\) 

\(\Rightarrow m=1\) (tm) 

b) Để đồ thị (1) tạo với trục Ox một góc \(\partial=30^o\) thì 

\(a=tan\partial\)

\(\Rightarrow2-m=tan30^o\)

\(\Rightarrow2-m=\dfrac{\sqrt{3}}{3}\)

\(\Rightarrow m=2-\dfrac{\sqrt{3}}{3}\)

\(\Rightarrow m=\dfrac{6-\sqrt{3}}{3}\left(tm\right)\) 

c) Để đồ thị (1) tạo với trục Ox một góc \(\partial=135^o\) thì:

\(a=tan\partial\)

\(\Rightarrow2-m=tan135^o\)

\(\Rightarrow2-m=-1\)

\(\Rightarrow m=2+1\)

\(\Rightarrow m=3\left(tm\right)\)

d) Để đường thẳng (1) cắt trục tung tại điểm có tung độ là 4 thì: (đk: \(m\ne1\) vì nếu bằng 1 thì (1) sẽ đi qua gốc tọa độ) 

Ta thay \(x=0\) và \(y=4\) vào (1) ta có: 

\(4=\left(2-m\right)+m-1\) 

\(\Rightarrow m-1=4\)

\(\Rightarrow m=4+1\)

\(\Rightarrow m=5\left(tm\right)\)

e) Để đường thẳng (1) cắt trục hành tại điểm có hoành độ bằng (-3) thì: (đk: \(m\ne1\))

Ta thay \(x=-3\) và \(y=0\) vào (1) ta có:

\(0=-3\cdot\left(2-m\right)+m-1\)

\(\Rightarrow-6+3m+m-1=0\)

\(\Rightarrow4m-7=0\) 

\(\Rightarrow4m=7\)

\(\Rightarrow m=\dfrac{7}{4}\left(tm\right)\)

ĐKXĐ: x ≠ 2

a) Đồ thị của hàm số đi qua gốc tọa độ nên m - 1 = 0

⇔ m = 1 (nhận)

Vậy m = 1 thì đồ thị của hàm số đi qua gốc tọa độ

b) Do đồ thị của hàm số tạo với trục Ox một góc ∂ = 30⁰ nên:

tan30⁰ = 2 - m

⇔ 2 - m = √3/3

⇔ m = 2 - √3/3 (nhận)

Vậy m = 2 - √3/3 thì đồ thị của hàm số đã cho tạo với trục Ox một góc 30⁰

c) Do đồ thị của hàm số tạo với trục Ox một góc ∂ = 135⁰

⇒ 2 - m = tan135⁰

⇔ 2 - m = -1

⇔ -m = -1 - 2

⇔ m = 3 (nhận)

Vậy m = 3 thì đồ thị của hàm số đã cho tạo với trục Ox một góc 135⁰

d) Do đường thẳng (1) cắt trục tung tại điểm có tung độ bằng 4 nên thay x = 0; y = 4 vào (1), ta có:

(2 - m).0 + m - 1 = 4

⇔ m = 4 + 1

⇔ m = 5 (nhận)

Vậy m = 5 thì đường thẳng (1) cắt trục tung tại điểm có tung độ bằng 4

e) Do đường thẳng (1) cắt trục hoành tại điểm có hoành độ bằng -3 nên thay x = -3; y = 0 vào (1) ta có:

(2 - m).(-3) + m - 1 = 0

⇔ -6 + 3m + m - 1 = 0

⇔ 4m - 7 = 0

⇔ 4m = 7

⇔ m = 7/4 (nhận)

Vậy m = 7/4 thì (1) cắt trục hoành tại điểm có hoành độ bằng -3

lỗi ảnh r pẹn 

a: 

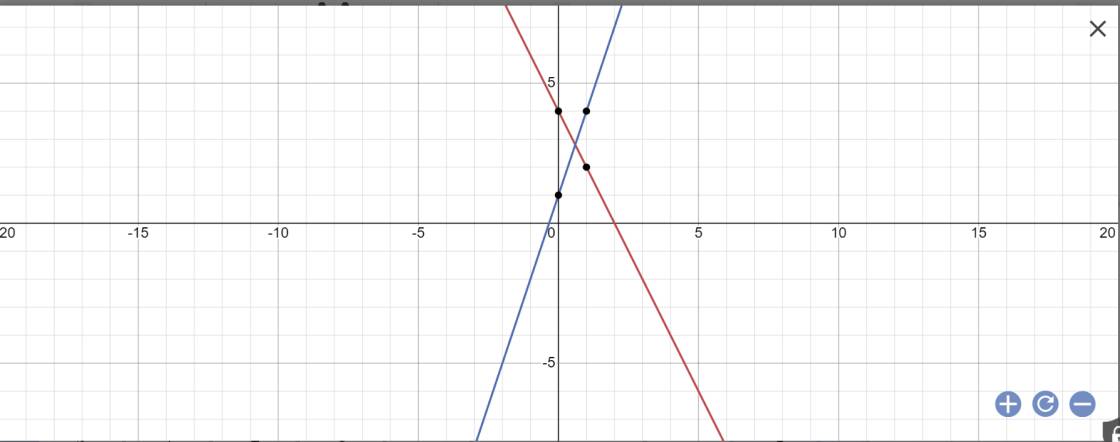
b: Phương trình hoành độ giao điểm là:

4-2x=3x+1

=>-2x-3x=1-4

=>-5x=-3

=>\(x=\dfrac{3}{5}\)

Thay x=3/5 vào y=3x+1, ta được:

\(y=3\cdot\dfrac{3}{5}+1=\dfrac{9}{5}+1=\dfrac{14}{5}\)

Vậy: \(N\left(\dfrac{3}{5};\dfrac{14}{5}\right)\)

c: (d'): y=3x+1

=>a=3

\(tan\alpha=a=3\)

=>\(\alpha\simeq71^034'\)

\(i=90^o-40^o=50^o\)

\(i=i'\Leftrightarrow i'=50^o\)

\(\Rightarrow\) Chọn đáp án B

Vì đường trung trực của `AC` cắt `AB` tại `D.`

`@` Theo tính chất của đường trung trực (điểm nằm trên đường trung trực của `1` đoạn thẳng thì cách `2` đầu mút đoạn thẳng đó)

`-> \text {DA = DC}`

Xét `\Delta ACD`: `\text {DA = DC}`

`-> \Delta ACD` cân tại `D.`

`-> \hat {A} = \hat {ACD}` `(1)`

Vì `\text {CD}` là tia phân giác của $\widehat {ACB} (g$$t)$
`->` $\widehat {ACD} = \widehat {BCD} =$ `1/2` $\widehat {ACB}$ `(2)`

Từ `(1)` và `(2)`

`->` $\widehat {ACB} = \widehat {2C_2} = \widehat {2A}$

Mà `\hat {A}=35^0`

`->` $\widehat {ACB}$`=35^0*2=70^0`

Xét `\Delta ABC`:

$\widehat {BAC} + \widehat {ABC}+ \widehat {ACB}=180^0 (\text {định lý tổng 3 góc trong 1 tam giác})$

`-> 35^0+` $\widehat {ABC} + 70^0=180^0$

`->` $\widehat {ABC}= 180^0-35^0-70^0=75^0$

Xét các đáp án trên `-> C (tm)`.

Hình:

Cho tam giác ABC có: góc A=35 độ. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. số đo các góc góc ABC; góc ACB là:
A. góc ABC= 72 độ; góc ACB= 73 độ
B. góc ABC= 73 độ; góc ACB= 72 độ
C. góc ABC= 75 độ; góc ACB= 70 độ
D. góc ABC= 70 độ; góc ACB=75 độ

Chọn B

b

a: 

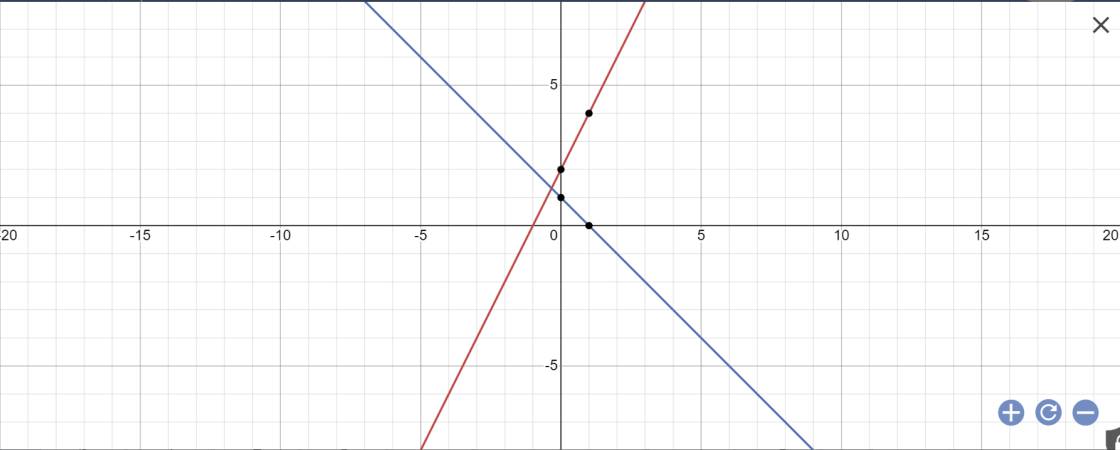
b: Phương trình hoành độ giao điểm là:

2x+2=-x+1

=>2x+x=1-2

=>3x=-1

=>\(x=-\dfrac{1}{3}\)

Khi x=-1/3 thì \(y=-\left(-\dfrac{1}{3}\right)+1=\dfrac{4}{3}\)

Vậy: \(M\left(-\dfrac{1}{3};\dfrac{4}{3}\right)\)

c: Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+1 với trục Ox

\(tan\alpha=a=1\)

=>\(\alpha=45^0\)

B. 50 độ.

b

B

C

C

A.30^o