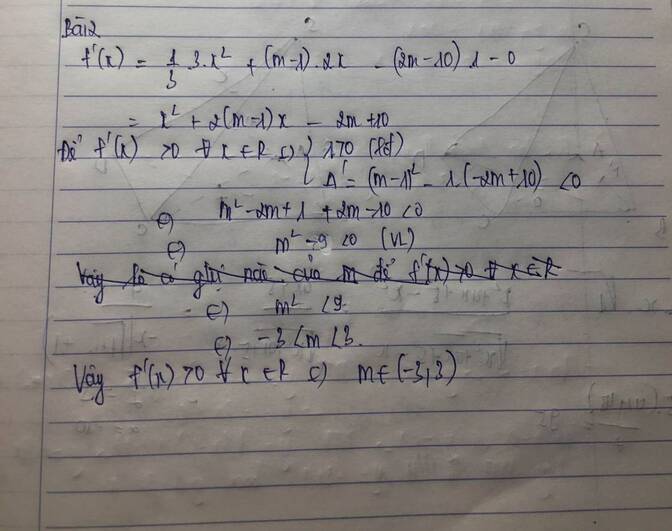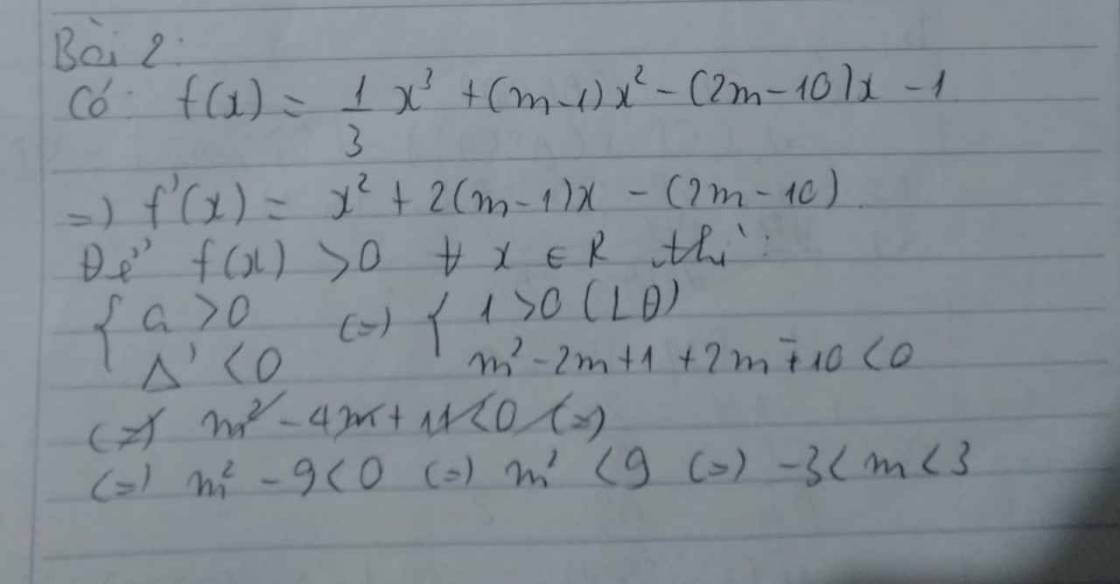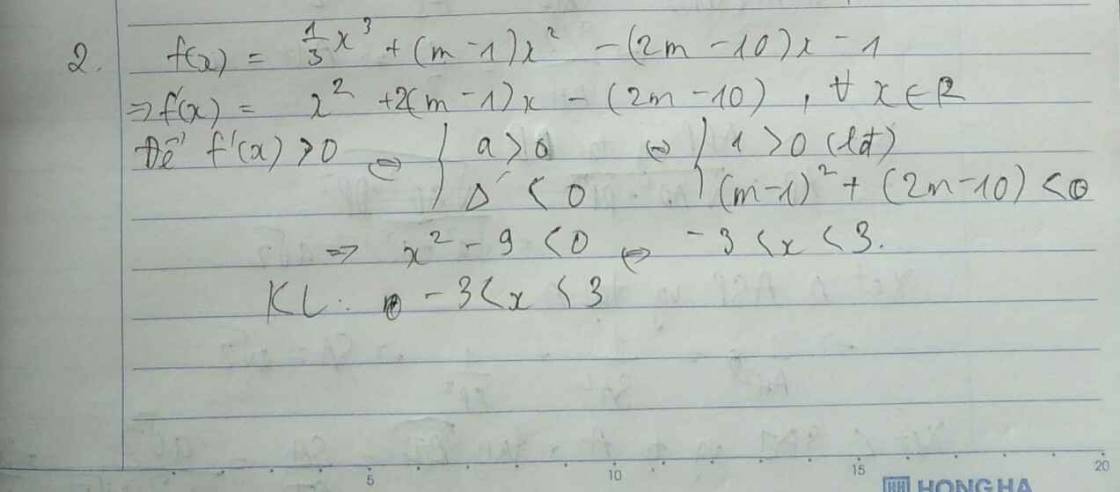tìm gtnn của biểu thức \(x^2+3\left|x\right|\) với \(x\in R\)

Những câu hỏi liên quan
Tìm GTNN của mỗi biểu thức sau:
a) \(P=\left(x+30\right)^2+\left(y-4\right)^2+1975 \)
b)\(Q=\left(3x+1\right)^2+\left|2y-\dfrac{1}{3}\right|+\sqrt{5}\)
c)\(R=\dfrac{3}{1-x-x^2}\)
3 câu này bạn áp dụng cái này nhé.
`a^2 >=0 forall a`.
`|a| >=0 forall a`.
`1/a` xác định `<=> a ne 0`.
Đúng 3
Bình luận (0)
a: P=(x+30)^2+(y-4)^2+1975>=1975 với mọi x,y
Dấu = xảy ra khi x=-30 và y=4
b: Q=(3x+1)^2+|2y-1/3|+căn 5>=căn 5 với mọi x,y
Dấu = xảy ra khi x=-1/3 và y=1/6
c: -x^2-x+1=-(x^2+x-1)
=-(x^2+x+1/4-5/4)
=-(x+1/2)^2+5/4<=5/4
=>R>=3:5/4=12/5
Dấu = xảy ra khi x=-1/2
Đúng 1
Bình luận (0)
Tìm GTLN và GTNN nếu có của các biểu thức sau :
a. \((x+\dfrac{2}{3})^2+\dfrac{1}{2}với(x\in Q)\)
b.\(\left|x-2020\right|+2021\)
Tìm GTNN của biểu thức :
\(A=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x+2\right)^2}\)
Tìm GTNN của biểu thức:
\(A=\dfrac{\left(x+5\right)\left(x-1\right)}{\left(x+3\right)^2}\)
Đặt \(x+3=t\ne0\Rightarrow x=t-3\)
\(A=\dfrac{\left(t+2\right)\left(t-4\right)}{t^2}=\dfrac{t^2-2t-8}{t^2}=-\dfrac{8}{t^2}-\dfrac{2}{t}+1=-8\left(\dfrac{1}{t}+\dfrac{1}{8}\right)^2+\dfrac{9}{8}\le\dfrac{9}{8}\)
\(A_{max}=\dfrac{9}{8}\) khi \(t=-8\) hay \(x=-11\)
Đúng 1
Bình luận (0)
Cho biểu thức $f\left( x \right)=\dfrac{1}{3}{{x}^{3}}+\left( m-1 \right){{x}^{2}}-\left( 2m-10 \right)x-1$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để ${f}'\left( x \right)>0$ $\forall x\in \mathbb{R}$.
Xem thêm câu trả lời
Tìm GTNN của biểu thức M
M = \(\left(x-1\right)^4+\left(3-x\right)^4+6\left(x^2-4x+3\right)^2+2013\)
Tìm GTNN của biểu thức: \(A=\dfrac{3\left|x+2\right|+1}{\left|x+2\right|+1}\)
tìm GTNN của biểu thức: A= \(\left|x-3\right|+\left|x-1\right|+\left|x+1\right|+\left|x+3\right|\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\):
\(A=\left|x-3\right|+\left|x-1\right|+\left|x+1\right|+\left|x+3\right|\)
\(=\left|3-x\right|+\left|x+3\right|+\left|1-x\right|+\left|x+1\right|\)
\(\ge\left|3-x+x+3\right|+\left|1-x+x+1\right|=8\)
\(minA=8\Leftrightarrow\left\{{}\begin{matrix}\left(3-x\right)\left(x+3\right)\ge0\\\left(1-x\right)\left(x+1\right)\ge0\end{matrix}\right.\Leftrightarrow-1\le x\le1\)
Đúng 1
Bình luận (0)
Tìm GTNN của biểu thức: A=\(\frac{x^2+2x+3}{\left(x+2\right)^2}\)
Giúp em vơi!!! Mốt thi r ạ!!!
GTNN là \(\frac{2}{3}\)đạt được khi x = 1
Đúng 0
Bình luận (0)
Điều kiện x # -2
Ta có
A(x2 + 4x + 4) = x2 + 2x + 3
<=> x2 (A - 1) + x(4A - 2) + 4A - 3 = 0
Để phương trình có nghiệm thì ∆' \(\ge0\)
<=> (2A - 1)2 - (A - 1)(4A - 3) \(\ge0\)
<=> 3A - 2\(\ge0\)
<=> A \(\ge\frac{2}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời