Tính tổng hoành độ các giao điểm của đồ thị hàm số y = 5 x + 6 x + 2 và đường thẳng y=-x
A. -7
B. -5
C. 5
D. 7
Tính tổng hoành độ các giao điểm của đồ thị hàm số y = 5 x + 6 x + 2 và đường thẳng y = - x
A. -7
B. -5
C. 5
D. 7
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số y = 5 x + 6 x + 2
và đường thẳng y = - x là:
![]()
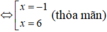
Tổng hoành độ các giao điểm là: 5
Câu 3: Cho các hàm số \(y=2x+5\) và \(y=-x+2\)
a. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng toạ độ Oxy.
b. Dựa vào hình vẽ, xác định toạ độ giao điểm A của hai đồ thị hàm số.
c. Hai đồ thị của hai hàm số đã cho cắt trục hoành tại các điểm B và C. Tính diện tích tam giác ABC
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m (Hình 37)
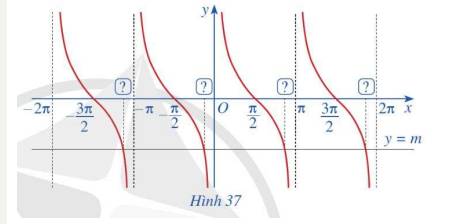
a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m trên khoảng \(\left( {0;\pi } \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.
b) Có nhận xét gì về nghiệm của phương trình cotx = m?
a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng\(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
GIÚP MÌNH GẤP VỚI Ạ, PLS.
a) Vẽ đồ thị hàm số y=3x-3.
b) Xác định hàm số y=3x-1+a, biết đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
c) Tìm tọa độ giao điểm của 2 đồ thị hàm số của câu a) và b) bằng phép tính.
\(b,\Leftrightarrow x=3;y=0\Leftrightarrow9-1+a=0\Leftrightarrow a=-8\\ \Leftrightarrow y=3x-1-8=3x-9\\ c,\text{PT hoành độ giao điểm: }3x-3=3x-9\Leftrightarrow0x=-6\Leftrightarrow x\in\varnothing\)
Vậy 2 đt trên không cắt nhau
Cho hàm số y=x² ; y=2x+3 a, vẽ các đồ thị trên cùng 1 mặt phẳng tọa độ b, tìm hoành độ giao điểm chung của 2 đồ thị
b: Hoành độ giao điểm chung là:
\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
Cho hàm số y=(m-1)x+m
a) Xác định m để đồ thị hàm số cắt trục tung điểm có tung độ bằng 3, cắt trục hoành tại điểm có hoành độ bằng 3
b) Vẽ đồ thị hàm số của hai hàm số ứng với m tìm được câu a
c) Gọi giao điểm của 2 đồ thị với trục hoành lần lượt là A;B giao điểm của 2 đồi thị là C. Tính chu vi và diện tích của tam giác ABC
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
Cho hàm số y = x 4 − 6 x 2 + 3 có đồ thị là (C) . Parabol P : y = − x 2 − 1 cắt đồ thị (C) tại bốn điểm phân biệt. Tổng bình phương các hoành độ giao điểm của P và (C)bằng:
A.5
B.10
C.8
D.4
Đáp án là B.
Phương trình hoành độ giao điểm của P và (C):
x 4 − 6 x 2 + 3 = − x 2 − 1 ⇔ x 4 − 5 x 2 + 4 = 0 ⇔ x 2 = 1 x 2 = 4 ⇔ x = ± 1 x = ± 2
Vậy ta có tổng bình phương các hoành độ giao điểm của P và (C): − 1 2 + 1 2 + − 2 2 + 2 2 = 10
Bài 6: a) Vẽ đồ thị của hàm số y = 3x + 1.
b) Xác định hàm số y = ax + b biết đồ thị của hàm số song song với đường thẳng y = 3x + 1 và cắt trục hoành tại điểm có hoành độ bằng -3.
c) Tìm tọa độ giao điểm của đường thẳng y = 3x + 1 và đường thẳng y = - x + 7
d) Tìm k để đồ thị của hai hàm số bậc nhất y = (k – 2)x – 3k + 4 và y = (2k + 1)x + k + 5 là hai đường thẳng song song
Đồ thị của hàm số \(y=ax+b\) song song với đường thẳng \(y=3x+1.\) \(\Rightarrow\left\{{}\begin{matrix}a=3.\\b\ne1.\end{matrix}\right.\) (1)
Đồ thị của hàm số \(y=ax+b\) cắt trục hoành tại điểm có hoành độ bằng \(-3.\) \(\Rightarrow\left\{{}\begin{matrix}x=-3.\\y=0.\end{matrix}\right.\) (2)
Thay (1); (2) vào hàm số \(y=ax+b\)\(:0=3.\left(-3\right)+b.\Leftrightarrow b=9\left(TM\right).\)
Vậy hàm số đó là: \(y=3x+9.\)
c) Xét phương trình hoành độ giao điểm của 2 đường thẳng \(y=3x+1;y=-x+7:\)
\(3x+1=-x+7.\Leftrightarrow4x=6.\Leftrightarrow x=\dfrac{3}{2}.\Rightarrow y=\dfrac{11}{2}.\)
Vậy tọa độ giao điểm của 2 đường thẳng đó là \(\left(\dfrac{3}{2};\dfrac{11}{2}\right).\)
Cho các hàm số: \(y=x^2\) và y=-x+2. Xác định tọa độ các giao điểm A, B của đồ thị hai hàm số đã cho và tọa độ trung điểm I của AB biết A có hoành độ dương
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+x-2=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=x^2\end{matrix}\right.\)
=>A(1;1); B(-2;4)
Tọa độ trung điểm I là:
\(\left\{{}\begin{matrix}x_I=\dfrac{1+\left(-2\right)}{2}=\dfrac{-1}{2}\\y_I=\dfrac{1+4}{2}=\dfrac{5}{2}\end{matrix}\right.\)