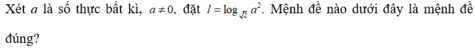
A. l = 4 log 2 a
B. l = 1 2 log 2 a
C. l = 1 2 log 2 a
D. l = 1 4 log 2 a
tính giá trị của biểu thức A=log32.log43.log54...log1615 là:
A.1 B.\(\dfrac{3}{4}\) C.\(\dfrac{1}{4} \) D.\(\dfrac{1}{2}\)
Lời giải:
Sử dụng công thức \(\log_ab=\frac{\ln b}{\ln a}\)
\(\Rightarrow A=\frac{\ln 2}{\ln 3}.\frac{\ln 3}{\ln 4}.\frac{\ln 4}{\ln 5}....\frac{\ln 15}{\ln 16}\)
\(\Leftrightarrow A=\frac{\ln 2}{\ln 16}=\log_{16}2=\frac{1}{4}\)
Đáp án C.
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
Tính giá trị của các biểu thức sau:
a) \(A = {\log _2}3.{\log _3}4.{\log _4}5.{\log _5}6.{\log _6}7.{\log _7}8;\)
b) \(B = {\log _2}2.{\log _2}4...{\log _2}{2^n}.\)
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
log9a=log12b=log16(a+b) mệnh đề đúng là :
a) \(\dfrac{a}{b}\in\left(\dfrac{2}{3};1\right)\) b)\(\dfrac{a}{b}\in\left(0;\dfrac{2}{3}\right)\) c)\(\dfrac{a}{b}\in\left(9;12\right)\) d)\(\dfrac{a}{b}\in\left(9;16\right)\)
Lời giải:
Đặt \(\log_9a=\log_{12}b=\log_{16}(a+b)=t\)
\(\left\{\begin{matrix} a=9^t\\ b=12^t\\ a+b=16^t\end{matrix}\right.\Rightarrow 9^t+12^t=16^t\)
Chia 2 vế cho \(12^t\) ta có:
\(\left(\frac{9}{12}\right)^t+1=\left(\frac{16}{12}\right)^t\)
\(\Leftrightarrow \left(\frac{3}{4}\right)^t+1=\left(\frac{4}{3}\right)^t\) (1)
Đặt \(\frac{a}{b}=\left(\frac{9}{12}\right)^t=\left(\frac{3}{4}\right)^t=k\). Thay vào (1):
\(k+1=\frac{1}{k}\Leftrightarrow k^2+k-1=0\)
\(\Leftrightarrow \frac{a}{b}=k=\frac{-1+ \sqrt{5}}{2}\) (do \(k>0\) nên loại TH \(k=\frac{-1-\sqrt{5}}{2}\) )
Thấy \(\frac{-1+\sqrt{5}}{2}\in (0;\frac{2}{3})\) nên chọn đáp án b
Cho phương trình: \(4.3^{log\left(100x^2\right)}+9.4^{log\left(10x\right)}=13.6^{1+log\left(x\right)}\) . Gọi a, b lần lượt là hai nghiệm của phương trình. Tìm tích ab.
A. ab = \(\dfrac{1}{10}\)
B. ab = 1
C. ab = 100
D. ab = 10
Đề bài
Cho \({\log _a}b = 2\). Tính:
a) \({\log _a}\left( {{a^2}b} \right)\)
b) \({\log _a}\frac{{a\sqrt a }}{{b\sqrt[3]{b}}}\)
c) \({\log _a}(2b) + {\log _a}\left( {\frac{{{b^2}}}{2}} \right)\)
a) \(\log_a\left(a^2b\right)=\log_aa^2+\log_ab=2.\log_aa+\log_ab=2.1+2=4\)
b) \(\log_a\dfrac{a\sqrt{a}}{b\sqrt[3]{a}}=\log_a\left(a\sqrt{a}\right)-\log_a\left(b\sqrt[3]{b}\right)=\log_aa^{\dfrac{3}{2}}-\log_ab^{\dfrac{4}{3}}=\dfrac{3}{2}.\log_aa-\dfrac{4}{3}\log_ab=\dfrac{3}{2}.1-\dfrac{4}{3}.2=-\dfrac{7}{6}\)
c) \(\log_a\left(2b\right)+\log_a\left(\dfrac{b^2}{2}\right)=\log_a2+\log_ab+\log_ab^2-\log_a2=\log_ab+2\log_ab=3\log_ab=3.2=6\)
a: \(=log_aa^2+log_ab=2+2=4\)
b: \(log_a\left(\dfrac{a\sqrt{a}}{b\sqrt[3]{b}}\right)=log_aa^{\dfrac{3}{2}}-log_ab^{\dfrac{4}{3}}\)
=3/2-4/3*2
=3/2-8/3
=9/6-16/6=-7/6
c: \(log_a\left(2b\right)+log_a\left(\dfrac{b^2}{2}\right)\)
\(=log_a\left(2b\cdot\dfrac{b^2}{2}\right)=log_a\left(b^3\right)=3\cdot2=6\)
Nếu \({a^{\frac{1}{2}}} = b\left( {a > 0,a \ne 1} \right)\) thì
A. \({\log _{\frac{1}{2}}}a = b\).
B. \(2{\log _a}b = 1\).
C. \({\log _a}\frac{1}{2} = b\).
D. \({\log _{\frac{1}{2}}}b = a\).
\({a^{\frac{1}{2}}} = b \Leftrightarrow {\log _a}b = \frac{1}{2} \Leftrightarrow 2{\log _a}b = 1\)
Chọn B.
1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)
Bài 3:
\(\log_{27}5=a; \log_87=b; \log_23=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln 27}=a; \frac{\ln 7}{\ln 8}=b; \frac{\ln 3}{\ln 2}=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln (3^3)}=a; \frac{\ln 7}{\ln (2^3)}=b; \ln 3=c\ln 2\)
\(\Leftrightarrow \frac{\ln 5}{3\ln 3}=a; \frac{\ln 7}{3\ln 2}=b; \ln 3=c\ln 2\)
\(\Rightarrow \frac{\ln 5}{3c\ln 2}=a; \frac{\ln 7}{3\ln 2}=b\)
\(\Rightarrow \ln 35=\ln 5+\ln 7=3ac\ln 2+3b\ln 2\)
Do đó:
\(D=\log_6 35=\frac{\ln 35}{\ln 6}=\frac{\ln 35}{\ln 2+\ln 3}=\frac{\ln 35}{\ln 2+c\ln 2}=\frac{3ac\ln 2+3b\ln 2}{\ln 2+c\ln 2}\)
\(=\frac{3ac+3b}{1+c}\)
Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
Cho \(0 < a \ne 1\). Tính giá trị của biểu thức \(B = {\log _a}\left( {\frac{{{a^2} \cdot \sqrt[3]{a} \cdot \sqrt[5]{{{a^4}}}}}{{\sqrt[4]{a}}}} \right) + {a^{2{{\log }_a}\frac{{\sqrt {105} }}{{30}}}}\).
\(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}=\dfrac{a^2\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{4}{5}}}{a^{\dfrac{1}{4}}}=\dfrac{a^{\dfrac{47}{15}}}{a^{\dfrac{1}{4}}}=a^{\dfrac{173}{60}}\)
\(\Rightarrow log_a\left(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}\right)=log_a\left(a^{\dfrac{173}{60}}\right)=\dfrac{173}{60}\)
\(a^{2log_a\left(\dfrac{\sqrt{105}}{30}\right)}=a^{log_a\left(\dfrac{7}{60}\right)}=\dfrac{7}{60}\)
Vậy \(B=\dfrac{173}{60}+\dfrac{7}{60}=\dfrac{180}{60}=3\)