Phương trình 7 2 x 2 + 6 x + 4 = 49 có tổng tất cả các nghiệm bằng
A.1
B. 5 2
C. -1
D. - 5 2
Phương trình -7x-14=-6x+18 tương đương với phương trình \(\dfrac{6}{x-2}\)=\(\dfrac{7}{-x-3}\)không?Vì sao?tìm 1 phương trình khác tương đương với phương trình \(\dfrac{6}{x-2}\)=\(\dfrac{7}{-x-3}\)
Hai phương trình này không tương đương vì chúng không có chung tập nghiệm
x2-4x+7 = 0 ⇔ x2 -4x + 4 + 3 = 0
⇔ (x-2)2+3=0 ⇔ (x-2)2=-3 (vô lí)
Vậy pt vô nghiệm
*Chứng minh phương trình \(x^2-4x+7=0\) vô nghiệm
Ta có: \(x^2-4x+7=0\)
\(\Leftrightarrow x^2-4x+4+3=0\)
\(\Leftrightarrow\left(x-2\right)^2+3=0\)
mà \(\left(x-2\right)^2+3\ge3>0\forall x\)
nên \(x\in\varnothing\)(đpcm)
Phương trình x2 – 5x + 6 = 0 có nghiệm là:
A/ x = - 2 ; x = 3 B/ x = - 2 ; x = -3 C/ x = 2 ; x = 3 D/ x = 2 ; x =-3
19/ Phương trình 3 – 7x = 0 có hệ số a, b bằng:
A/ a = 7 ; b = 3 B/ a = 3 ; b = 7 C/ a = -7 ; b = -3 D/ a = - 7; b = 3
20/ Phương trình 5x + 3 = 5x - 3 có nghiệm là:
A/ vô nghiệm B/ vô số nghiệm C/ x = 0 D/ x = \(x=-\dfrac{3}{5}\)
a) Cho phương trình $x^{2}-m x-10 m+2=0$ có một nghiệm $x_{1}=-4$. Tìm $m$ và nghiệm còn lại.
b) Cho phương trình $x^{2}-6 x+7=0 .$ Không giải phương trình, hãy tính tổng và tích của hai nghiệm của phương trình đó.
a, Do \(x=-4\)là một nghiệm của pt trên nên
Thay \(x=-4\)vào pt trên pt có dạng :
\(16+4m-10m+2=0\Leftrightarrow-6m=-18\Leftrightarrow m=3\)
Thay m = 3 vào pt, pt có dạng : \(x^2-3x-28=0\)
\(\Delta=9-4.\left(-28\right)=9+112=121>0\)
vậy pt có 2 nghiệm pb : \(x_1=\frac{3-11}{2}=-\frac{8}{2}=-4;x_2=\frac{3+11}{2}=7\)
b, Theo Vi et : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=6\\x_1x_2=\frac{c}{a}=7\end{cases}}\)
Vậy m=3, và ngiệm còn lại x2=7
a)
m = 3
x2=7
giải phương trình: (x+3/x-2)^2 + 6(x-3/x+2)^2 = 7(x^2-9)/x^2-4
3.15 giải các phương trình sau :
a) ( x - 6 ) ( 2x - 5 ) ( 3x + 9 ) = 0
b) 2x( x - 3 ) + 5( x - 3 ) = 0
c) ( x^2 - 4 ) - ( x - 2 ) ( 3 - 2x ) =0
3.16 tìm m để phương trình sau có nghiệm :
x=-7 ( 2m - 5 )x - 2m^2 + 8
3.17 giải các phương trình sau :
a) ( 2x - 1 )^2 - ( 2x + 1 ) = 0
\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)
\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)
\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)
\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)
\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
3.15:
a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)
b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3.16
\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)
\(\Leftrightarrow-14m+35-2m^2+8=0\)
\(\Leftrightarrow-14m-2m^2+43=0\)
\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)
\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)
\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)
\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)
pt vô nghiệm
Giải các bất phương trình sau:
a) \(7{x^2} - 19x - 6 \ge 0\)
b) \( - 6{x^2} + 11x > 10\)
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1\)
d) \({x^2} - 10x + 25 \le 0\)
a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
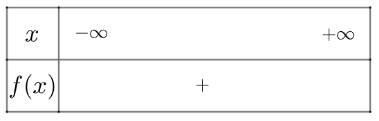
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)
Câu 1 Mã: 78331
Giải bất phương trình 2x+1x+2≤12x+1x+2≤1
−2≤x≤−1−2≤x≤−1
−2≤x<1−2≤x<1
−2<x≤1−2<x≤1
Vô nghiệm
Câu 2 Mã: 78319
Bất phương trình (3x+1)(6-5x)(3x-7)<0, tập nghiệm của bất phương trình là:
S={x |−13<x<65−13<x<65}
S={x| x>73x>73 }
S={x| −13≤x≤65−13≤x≤65 hoặc x>73x>73 }
S={x| −13<x<65−13<x<65 hoặc x>73x>73 }
Câu 3 Mã: 78314
Tập nghiệm của bất phương trình tích (x+3)(x-7)
S={x\-3 < x hoặc x < 7}
S={x\-3 < x < 7}
S={x\-3 > x > 7}
S={-3;7}
Câu 4 Mã: 78328
Giải bất phương trình: 3xx−3>3x−1x−33xx−3>3x−1x−3
x>−3x>−3
x≥−3x≥−3
x>3x>3
x≥3x≥3
Câu 5 Mã: 78330
Giải bất phương trình: 1x+4≤1x−21x+4≤1x−2
x≥2x≥2
x≤−4x≤−4
x≥2x≥2 hoặc x≤−4x≤−4
x≥2x≥2 vàx≤−4x≤−4
Câu 6 Mã: 78316
Bất phương trình (2x-3)(x22+1)≤0≤0. Tập nghiệm của bất phương trình là:
S={x\x≤32≤32}
S={x\x≥32≥32}
S={x\x<32<32}
Đáp án khác
Câu 7 Mã: 78332
Số nghiệm nguyên thỏa mãn bất phương trình (x+5)(7−2x)>0(x+5)(7−2x)>0
8
7
9
10
Câu 8 Mã: 78321
Tìm x sao cho (x-2)(x-5)>0
x>5 và x<2
x>2
x>5 hoặc x<2
x>5
Câu 9 Mã: 78327
Có bao nhiêu giá trị x nguyên thỏa mãn bất phương trình: x−3x+5+x+5x−3<2x−3x+5+x+5x−3<2
4
5
3
6
Câu 10 Mã: 78315
Cho bất phương trình -2x22+11x-15>0. Giá trị x nguyên thỏa mãn bất phương trình là:
x=3
x=2
x=-2
không có giá trị x nào thỏa mãn
Câu 11 Mã: 78318
Cho bất phương trình: (2x+3)(x+1)(3x+5)≥≥ 0, tập nghiệm của bất phương trình là:
S={x | −53≤x≤−32−53≤x≤−32}
S={x | x≥−1x≥−1}
S={x| −53≤x≤−32−53≤x≤−32 hoặc x≥−1x≥−1}
S={x| −53<x<−32−53<x<−32 hoặc x>−1x>−1}
Câu 12 Mã: 78322
Tìm x sao cho x+2x−5<0x+2x−5<0
−2<x<4−2<x<4
−2<x<5−2<x<5
x<5x<5
x>−2x>−2
Câu 13 Mã: 78326
Giải bất phương trình: 4x+32x+1<24x+32x+1<2
x=−12x=−12
x≠−12x≠−12
x>−12x>−12
x<−12x<−12
Câu 14 Mã: 78313
Tập nghiệm của bất phương trình (x-1)(x+2)>0 là:
S={x/x<1 hoặc x>-2}
S={x/x<-2 hoặc x>1}
S={x/x>1 hoặc x<-2}
S={x/x>-2 hoặc x<1}
Câu 15 Mã: 78320
Bất phương trình (2x+1)(x2−4)>0(2x+1)(x2−4)>0 có tập nghiệm là:
S={x| -2 < x < −12−12 hoặc x>2}
S={x | -2 < x < −12−12 hoặc x≥≥ 2}
S={x | -2≤≤ x < −12−12 hoặc x>2}
S={x | -2 < x < −12−12 hoặc x=2}
Câu 16 Mã: 78329
Giải bất phương trình sau: 3x−4x+2≥03x−4x+2≥0
2<x<122<x<12
−12≤x≤−2−12≤x≤−2
x≤−2x≤−2
2≤x≤122≤x≤12
Câu 17 Mã: 78317
Cho bất phương trình:x2−4x+4≤0x2−4x+4≤0 , tập nghiệm của bất phương trình là:
S={x\x≤≤ 2}
S={2}
S={x\x< 2}
Đáp án khác
Câu 18 Mã: 78325
Tìm nghiệm nguyên dương của bất phương trình:
x2−2x−4(x+1)(x−3)>1x2−2x−4(x+1)(x−3)>1 (1)
x∈{1}x∈{1}
x∈{2}x∈{2}
x∈{1;2}x∈{1;2}
Vô nghiệm
Câu 19 Mã: 78324
Giải bất phương trình: (x−4)(9−x)≥0(x−4)(9−x)≥0
x≥4x≥4
x<9x<9
4≤x≤94≤x≤9
Vô nghiệm
Câu 20 Mã: 78323
Bất phương trình x2−2x+1<9x2−2x+1<9
−2<x<4−2<x<4
−2≤x<4−2≤x<4
−2<x<6−2<x<6
−2<x≤6
Tìm ĐIỀU KIỆN XÁC ĐỊNH của phương trình \(\dfrac{x}{2\left(x-3\right)}\)+\(\dfrac{x}{2\left(x+1\right)}\)=\(\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)và phương trình \(\dfrac{6}{x-2}\)=\(\dfrac{7}{-x-3}\)
+ Pt thứ nhất :
Ta có mẫu thức chung là : \(2\left(x-3\right)\left(x+1\right)\)
\(\Rightarrow\left[{}\begin{matrix}x\ne2\\x-3\ne0\\x+1\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne3\\x\ne-1\end{matrix}\right.\)
Vậy \(ĐKXĐ\) là :\(x\ne2;3;-1\)
+ Pt thứ hai :
Ta có mẫu thức chung là : \(\left(x-2\right)\left(x+3\right)\)
\(\Rightarrow\left[{}\begin{matrix}x-2\ne0\\x+3\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne-3\end{matrix}\right.\)
Vậy \(DKXD:\) \(\) \(x\ne2;-3\)
Giải phương trình sau: 6(x-7)=5(x+2) +x