Cho đồ thị ( C ) : y = 2 x - 3 x - 2 và đường thẳng (d): 5x + y - 1 = 0 . Goi k là số tiếp tuyến của (C) vuông góc với (d). Xác định k.
![]()
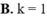
![]()
![]()
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số y=1/3x a)Đ nào thuộc đồ thị, không thuộc đồ thị A(1;2/3);B(-1;-1/3);C(2;-2/3);D(2;2/3) b)Tìm E(x;-1);F(-4;y) c) Vẽ đồ thị c)Vẽ đồ thị!!!!!

Cái câu vẽ đồ thị thì bạn chỉ cần lập bảng giá trị rồi biễu diễn trên hệ trục tọa độ Oxy là được
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
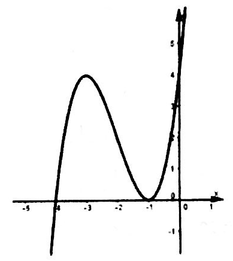
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
cho hs: y=\(\frac{2}{3}x^2-\frac{8}{3}x+2\) có đồ thị (P)
a) vẽ đồ thị (P)
b) Tìm x để hs đạt GTNN
c) Dựa vào đồ thị hàm số tìm x để y>0, y<0

b/ \(y=\frac{2}{3}x^2-\frac{8}{3}x+2=\frac{2}{3}\left(x-2\right)^2-\frac{2}{3}\ge-\frac{2}{3}\)
\(\Rightarrow y_{min}=-\frac{2}{3}\) khi \(x=2\)
c/ Nhìn vào đồ thị ta thấy:
- Để \(y>0\Rightarrow\left[{}\begin{matrix}x< 1\\x>3\end{matrix}\right.\)
- Để \(y< 0\Rightarrow1< x< 3\)
Cho hàm số y=1/3x a)Đ nào thuộc đồ thị, không thuộc đồ thị A(1;2/3);B(-1;-1/3);C(2;-2/3);D(2;2/3) b)Tìm E(x;-1);F(-4;y) c) Vẽ đồ thị
a: Các điểm B;D thuộc đồ thị, còn A,C không thuộc đồ thị
b: Thay y=-1 vào y=1/3x, ta được:
1/3x=-1
hay x=-3
Vậy: E(-3;-1)
Thay x=-4 vào y=1/3x, ta được:
y=-1/3x4=-4/3
Vây: F(-4;-4/3)
Cho đồ thị (C):y=x^3-3x^2+x+1 Tiếp tuyến của đồ thị (C) tại điểm M có hoành độ x = 0 cắt đồ thị (C) tại điểm N (khác M). Tìm tọa độ điểm N
A. N(4;-3)
B. N(1;0)
C. N(3;4)
D. N(-1;-4)
Đáp án C
Ta có: ![]()
Suy ra PTTT của (C) tại M là ![]()
Khi đó PT hoành độ giao điểm của (C) và ![]() là:
là: ![]()
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
cho hàm số y = (3 - m)x + m - 1 có đồ thị (d)
1) xác định m để (d) song song với đồ thị hàm số y = 2x + 3
2) Xác định m để (d) cắt đồ thị hàm số y = x + 3m - 2 tại một điểm trên trục tung
1) Để \(d//y=2x+3\)
\(\Rightarrow\left\{{}\begin{matrix}3-m=2\\3-1\ne3\end{matrix}\right.\)
\(\Leftrightarrow m=1\)
\(\Rightarrow d:y=2x\)
2) Tọa độ giao điểm của \(y=\left(3-m\right)x+3-1\) và \(y=x+3m-2\)là nghiệm của hệ phương trình.
\(\left\{{}\begin{matrix}y=\left(3-m\right)x+m-1\\y=x+3m-2\end{matrix}\right.\)
Mà chúng cắt nhau tại 1 điểm trên trục tung
\(\Rightarrow\left(3-m\right)0+m-1=0+3m-2\)
\(\Leftrightarrow m-1=3m-2\)
\(\Leftrightarrow m=\frac{1}{2}\)
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3