Cho a, b thuộc Z sao cho a3 + b3 = 20162017
CMR : a + b chia hết cho 3
Ai đúng tớ tick cho !!
cho a3+b3=2(c3-8d3); a,b,c,d ∈Z. CM a+b+c+d chia hết cho 3
Lời giải:
$a^3+b^3=2(c^3-8d^3)$
$a^3+b^3+c^3+d^3=c^3+d^3+2(c^3-8d^3)$
$=3c^3-15d^3=3(c^3-5d^3)\vdots 3$
Khi đó:
$(a+b+c+d)^3=(a+b)^3+(c+d)^3+3(a+b)(c+d)(a+b+c+d)$
$=a^3+b^3+c^3+d^3+3ab(a+b)+3cd(c+d)+3(a+b)(c+d)(a+b+c+d)\vdots 3$ do:
$a^3+b^3+c^3+d^3\vdots 3$
$3ab(a+b)\vdots 3$
$3cd(c+d)\vdots 3$
$3(a+b)(c+d)(a+b+c+d)\vdots 3$
Vậy:
$(a+b+c+d)^3\vdots 3$
$\Rightarrow a+b+c+d\vdots 3$
Cho a,b thuộc Z. CMR:a^2-17ab+b^2 chia hết cho 25<=>a chia hết cho 5 và b chia hết cho 5.
Giúp mk nha, ai nhanh+đúng mk tick!!!!!!!!
Cho 3 số nguyên dương a, b, c thỏa mãn a3 + b3 + c3 chia hết cho 14
CMR abc cũng chia hết cho 14
Rõ ràng trong hai số a, b, c tồn tại một số chẵn (Vì nếu a, b, c đều lẻ thì a3 + b3 + c3 là số lẻ, không chia hết cho 14).
Ta lại có \(a^3;b^3;c^3\equiv0;1;-1\).
Do đó nếu a, b, c đều không chia hết cho 7 thì \(a^3;b^3;c^3\equiv1;-1\left(mod7\right)\Rightarrow a^3+b^3+c^3⋮̸7\).
Làm tiếp: Suy ra trong ba số a, b, c có ít nhất một số chia hết cho 7 \(\Rightarrow abc⋮7\).
Vậy abc chia hết cho 14.
a) Chứng minh rằng: a3- a chia hết cho 6 với mọi giá trị a thuộc Z
b)Cho a,b,c thuộc Z thỏa mãn: a+b+c= 450 mũ 2023. Chứng minh rằng: a2+b2+c2 chia hết cho 6
a: a^3-a=a(a^2-1)
=a(a-1)(a+1)
Vì a;a-1;a+1 là ba số liên tiếp
nên a(a-1)(a+1) chia hết cho 3!=6
=>a^3-a chia hết cho 6
Đây là bài toán nâng cao lớp 6, mong các bạn giải giúp tớ nhé vì thứ 5 nộp rồi.
Câu 1: Cho x,y sao cho x + 1/y và y + 1/x thuộc Z
a) CMR: x2y2 + 1/x2y2 thuộc Z
b) Tìm tất cả số nguyên n sao cho: xnyn + 1/xnyn thuộc Z
Câu 2: CMR: a3 - a luôn chia hết cho 6
Các bạn giúp tớ nhé!!!!! Ai nhanh và đúng tớ tick cho(Nói trước là tớ không biết kết quả của bài này)
Cho các số nguyên a, b, c, d thỏa mãn a3+b3=5(c3+7d3). CMR a+b+c+d chia hết cho 6
Tìm x thuộc Z, để
a) 5x + 6 chia hết cho x+1
b) 5x + 3 chia hết cho x+1
c) x + 5 chia hết cho x+1
Giúp tớ nhé! Có gì tớ tick cho! Cảm ơn nhìu!
a. 5x+6 chia hết cho x+1
=> 5x+5+1 chia hết cho x+1
=> 5.(x+1)+1 chia hết cho x+1
Mà 5.(x+1) chia hết cho x+1
=> 1 chia hết cho x+1
=> x+1 \(\in\)Ư(1)={-1;1}
=> x \(\in\){-2; 0}.
b. 5x+3 chia hết cho x+1
=> 5x+5-2 chia hết cho x+1
=> 5.(x+1)-2 chia hết cho x+1
=> 2 chia hết cho x+1
=> x+1 \(\in\)Ư(2)={-2; -1; 1; 2}
=> x \(\in\){-3; -2; 0; 1}.
c. x+5 chia hết cho x+1
=> x+1+4 chia hết cho x+1
=> 4 chia hết cho x+1
=> x+1 \(\in\)Ư(4)={-4; -2; -1; 1; 2; 4}
=> x \(\in\){-5; -3; -2; 0; 1; 3}.
Trong không gian với hệ tọa độ Oxy, cho đường thẳng d : x - 1 1 = y - 1 2 = z - 1 2 , A(2;1;4). Gọi H(a,b,c) là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính T = a 3 + b 3 + c 3
A. T = 8
B. T = 62
C. T = 13
D. T = 5
Đáp án B.
Phương trình tham số của đường thẳng
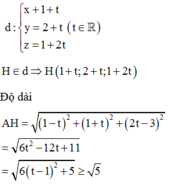
Độ dài AH nhỏ nhất bằng 5 khi
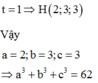
Trong không gian với hệ tọa độ Oxy, cho đường thẳng d: x - 1 1 = y - 2 1 = z - 1 2 ,A(2;1;4). Gọi H(a,b,c) là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính T = a 3 + b 3 + c 3
A. T=8
B. T=62
C. T=13
D. T= 5