Cho hình vẽ bên. Chứng minh: GI=HK

Những câu hỏi liên quan
Cho hình bên, trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK; AH = BK
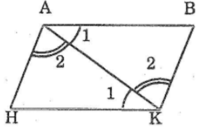
Nối AK, ta có:
AB // HK (giả thiết)
⇒ ∠(A1 ) =∠(K1 ) (hai góc so le trong)
+) Lại có: AH // BK (giả thiết)
⇒ ∠ (A2 ) = ∠(K2 ) (hai góc so le trong)
Xét ΔABK và ΔKHA, ta có:
∠(A1 ) =∠(K1 ) ( chứng minh trên)
AK cạnh chung
∠(K2 ) =∠(A2 ) (chứng minh trên)
Suy ra: ΔABK =ΔKHA (g.c.g)
Vậy: AB = KH; BK = AH ( 2 cạnh tương ứng)
Đúng 0
Bình luận (0)
Bài 3: Trong hình bên; chứng minh;HK là đường trung bình của tam giác ABC C A B K H Bài 4:(hs tự vẽ hình) Cho M;N là lần lượt trung điểm của 2 cạnh AB VÀ AC của tam giác ABC a. Tính các tỉ số AM/AB;AN/NC b. Chứng minh MN//BCC. chứng minh MN/BC1/2Bài 5: Trong hình bên cho biết AB10cm;DE6;5cm;EC3;7cm.Tính AD;EF;DF;BC Bài 6: Cho DE là đường trung bình của mỗi tam giác ABC trong hình bên dưới hãy tính giá trị x trong mỗi hình
Đọc tiếp
Bài 3: Trong hình bên; chứng minh;HK là đường trung bình của tam giác ABC
Bài 4:(hs tự vẽ hình) Cho M;N là lần lượt trung điểm của 2 cạnh AB VÀ AC của tam giác ABC
a. Tính các tỉ số AM/AB;AN/NC
b. Chứng minh MN//BC
C. chứng minh MN/BC=1/2
Bài 5: Trong hình bên cho biết AB=10cm;DE=6;5cm;EC=3;7cm.Tính AD;EF;DF;BC
Bài 6: Cho DE là đường trung bình của mỗi tam giác ABC trong hình bên dưới hãy tính giá trị x trong mỗi hình
Bài 3:
Xét ΔABC có
H là trung điểm của BA
HK//AC
Do đó: K là trung điểm của BC
Xét ΔBAC có
H,K lần lượt là trung điểm của BA,BC
=>HK là đường trung bình của ΔBAC



Đúng 0
Bình luận (0)
Bài 1:Cho tứ giác ABCD, M, N, I, K lần lượt là trung điểm AB, BC, CD, DA. Chứng minh MNIK là hình bình hành.Bài 2. Cho điểm D nằm bên trong tam giác đều ABC. Vẽ các tam giác đều BDE, CDF (E, F, D nằm cùng phía đối với BC). Chứng minh rằng AEDF là hình bình hành.Bài 3. Cho hình bình hành ABCD, hai đường chéo không vuông góc với nhau. Vẽ điểm E đối xứng với A qua BD. Chứng minh rằng 4 điểm B, C, E, D là 4 đỉnh của một hình thang cân.Help me, mai đi hk r
Đọc tiếp
Bài 1:Cho tứ giác ABCD, M, N, I, K lần lượt là trung điểm AB, BC, CD, DA. Chứng minh MNIK là hình bình hành.
Bài 2. Cho điểm D nằm bên trong tam giác đều ABC. Vẽ các tam giác đều BDE, CDF (E, F, D nằm cùng phía đối với BC). Chứng minh rằng AEDF là hình bình hành.
Bài 3. Cho hình bình hành ABCD, hai đường chéo không vuông góc với nhau. Vẽ điểm E đối xứng với A qua BD. Chứng minh rằng 4 điểm B, C, E, D là 4 đỉnh của một hình thang cân.
Help me, mai đi hk r
nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
Đúng 0
Bình luận (4)
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)
Đúng 0
Bình luận (1)
3) Vẽ tam giác ABC có A = 90độ , kẻ HA vuông góc với HK .Trên tia AH lấy K sao cho HA = HK
a) Chứng minh tam giác AHC = tam giác KHC và AC = HC .
b) Chứng minh tam giác ABC= tam giác KBC = 90độ .
Cho GHIK là hình bình hành. Chứng minh:
a, ABCD là hình bình hành
b,AC, BD, HK, GI đồng quy
Ta có: GD+DK=GK
IB+HB=IH
mà GK=IH
và DK=HB
nên GD=IB
Ta có: GA+AH=GH
CI+KC=KI
mà GH=KI
và GA=CI
nên AH=KC
Xét ΔAGD và ΔCIB có
AG=CI
\(\widehat{G}=\widehat{I}\)
GD=IB
Do đó: ΔAGD=ΔCIB
Suy ra: AD=CB
Xét ΔAHB và ΔCKD có
AH=CK
\(\widehat{H}=\widehat{K}\)
HB=KD
Do đó: ΔAHB=ΔCKD
Suy ra: AB=CD
Xét tứ giác ABCD có
AB=CD
AD=CB
Do đó: ABCD là hình bình hành
Đúng 0
Bình luận (0)
cho hình vẽ bên biết ac = ec , bc = cd.
a) chứng minh abc = edc
b) chứng minh ab = ed
Cho hình vẽ bên,biết EA EB; FA FB; QA QB.a) Vẽ lại hình và viết giả thiết, kết luận;b) Chứng minh ∆AEF ∆BEFc) Chứng minh ∆AEQ ∆BEQ;d) Chứng minh EQ là tia phân giác của góc AEB.
Đọc tiếp
Cho hình vẽ bên,biết EA = EB; FA = FB; QA = QB.
a) Vẽ lại hình và viết giả thiết, kết luận;
b) Chứng minh ∆AEF = ∆BEF
c) Chứng minh ∆AEQ = ∆BEQ;
d) Chứng minh EQ là tia phân giác của góc AEB.
Cho tam giác nhọn ABC.
a) Vẽ H là hình chiếu của B trên đường thẳng AC;
b) Vẽ K là hình chiếu của H trên đường thẳng AB;
c) Chứng minh rằng: HK < BH < BC.
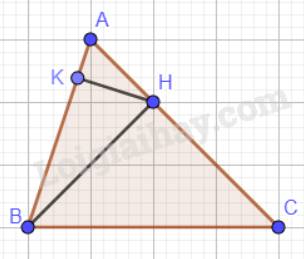
a) H là hình chiếu của B trên đường thẳng AC;
b) K là hình chiếu của H trên đường thẳng AB;
c) Trong tam giác ABC có: \(BH \bot AC\) nên BH < BC (BH là đường vuông góc, BC là đường xiên).
Trong tam giác AHB có: \(KH \bot AB\) nên HK < HB (HK là đường vuông góc, HB là đường xiên).
Vậy: HK < BH < BC.
Đúng 0
Bình luận (0)
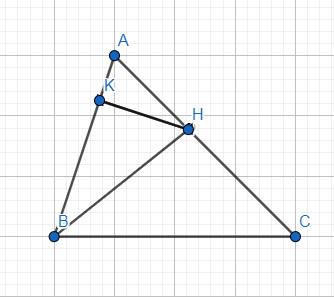
a) \(H\) là hình chiếu của \(B\) trên đường thẳng \(AC\);
b) \(K\) là hình chiếu của \(H\) trên đường thẳng \(AB\);
c) Trong tam giác \(ABC\) có: \(\text{BH < BC}\) (\(BH\) là đường vuông góc, \(BC\) là đường xiên).
Trong tam giác \(AHB\) có: \(\text{HK < HB}\) (\(HK\) là đường vuông góc, \(HB\) là đường xiên).
Vậy: \(\text{HK < BH < BC}\).
Đúng 0
Bình luận (0)
Cho hình vẽ mô tả thí nghiệm: Hinh vẽ bên mô tả thí nghiệm chứng minh A. tính tan nhiều trong nước của NH3. B. tính tan nhiều trong nước của HCI. C. khả năng phản ứng mạnh với nước của HCl. D. khả năng phản ứng mạnh với nước của NH3.
Đọc tiếp
Cho hình vẽ mô tả thí nghiệm:
Hinh vẽ bên mô tả thí nghiệm chứng minh
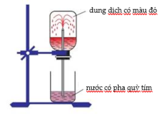
A. tính tan nhiều trong nước của NH3.
B. tính tan nhiều trong nước của HCI.
C. khả năng phản ứng mạnh với nước của HCl.
D. khả năng phản ứng mạnh với nước của NH3.






















