Với giá trị nào của x thì hàm số y = 2 2 log 3 x - log 3 x 2 đạt giá trị lớn nhất?
A. 2
B.3
C.1
D.2
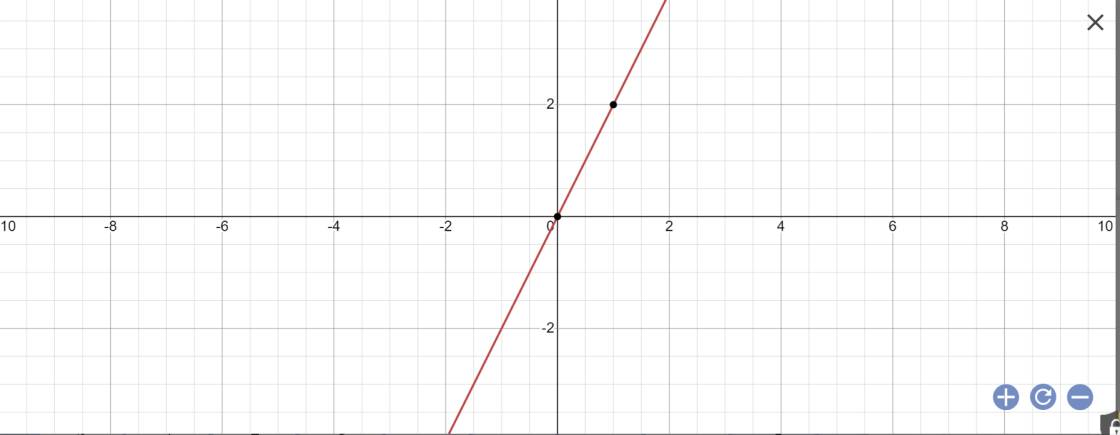
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Cho 2 hàm số bậc nhất y = (3m - 1)x + 2 và y = (m + 3)x +1
a) Với giá trị nào của m thì đồ thị của 2 hàm số là 2 đường thẳng song song với nhau?
b) Với giá trị nào của m thì đò thị của 2 hàm số là 2 đường thẳng cắt nhau?
\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)
Với giá trị nào của m thì hàm số sau đây là hàm số bậc nhất
a, y=\(\sqrt{m-3}\times x+\dfrac{2}{3}\)
b, y= \(\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\times x+2010\)
với giá trị nào của m thì hàm số ở ý a là hàm số đồng biến. Với gtri nào của m thì hàm số ở ý b là hàm nghịch biến
a) Ta có: \(y=\sqrt{m-3}\cdot x+\dfrac{2}{3}\left(m\ge3\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m-3}\ne0\Leftrightarrow m=3\)
Do: \(\sqrt{m-3}\ge0\forall m\ge3\)
Nên với \(m\ge3\) thì y đồng biến trên R
b) Ta có: \(y=\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\cdot x+2010\left(m\ge0;m\ne5\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m}-\sqrt{5}\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\ne5\end{matrix}\right.\)
Do \(\sqrt{m}+\sqrt{5}>0\Rightarrow\sqrt{m}-\sqrt{5}< 0\Leftrightarrow m< 5\)
Vậy với 0 ≤ m < 5 thì y nghịch biến trên R
a) Để hàm số là hàm số bậc nhất thì:
√(m - 3) > 0
⇔ m - 3 > 0
⇔ m > 3
Vậy với m > 3 thì hàm số đã cho là hàm bậc nhất
b) Để hàm số là hàm bậc nhất thì √m - √5 ≠ 0 và m ≥ 0
⇔ √m ≠ √5
⇔ m ≠ 5
Vậy m ≠ 5 và m ≥ 0 thì hàm số đã cho làm hàm số bậc nhất
*) Để hàm số ở câu a là hàm đồng biến thì m > 3
*) Để hàm số ở câu b là hàm nghịch biến thì √m < √5
⇔ 0 \(\le\) m < 5
Vậy 0 \(\le\) m < 5 thì hàm số ở câu b là hàm số nghịch biến
a) Tính \(y = {\log _2}x\) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của \(y = {\log _2}x\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {\log _2}x\) có nghĩa?
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
Bài 1 : Cho hàm số y=(m-3)x+4 . Với giá trị nào của m thì hàm số đồng biến, nghịch biến Bài 4: Cho hàm số y=(3-√2) x+1 a, Hàm số đồng biến hay nghịch biến? Vì sao? b, Tính các giá trị tương ứng của y khi x nhân các giá trị sau ; O, 1, √2, 3+√2, 3-√2
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
Cho hai hàm số y = (m - 1)x + 3 và y = (3 - m)x + 1, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhaub, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)
a, Với giá trị nào của a thì hàm số y = (a + b) x + 5 đồng biến
b, Với giá trị nào của k thì hàm số : y = (1 - \(k^2\)) x - 1 nghịch biến
b)
Để hàm số \(y=\left(1-k^2\right)x-1\) là hàm số bậc nhất thì \(1-k^2\ne0\)
\(\Leftrightarrow k^2\ne1\)
hay \(k\notin\left\{1;-1\right\}\)
Để hàm số \(y=\left(1-k^2\right)x-1\) nghịch biến trên R thì \(1-k^2< 0\)
\(\Leftrightarrow k^2>1\)
\(\Leftrightarrow\left[{}\begin{matrix}k>1\\k< 1\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được: \(\left[{}\begin{matrix}k>1\\k< 1\end{matrix}\right.\)
Vậy: Khi \(\left[{}\begin{matrix}k>1\\k< 1\end{matrix}\right.\) thì hàm số \(\left[{}\begin{matrix}k>1\\k< 1\end{matrix}\right.\) nghịch biến trên R
Cho hai hàm số bậc nhất y=(k+1)x+2 và y=(3-k) x-2) a) Với giá trị nào của k thì thì đồ thị của hai hàm số là hai đường thẳng song song với nhau? b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau? c) Hai đường thẳng nói trên có thể trùng nhau được không? Vì sao?
Câu 3: cho hàm số y = ( m - 3 ) x a, Với giá trị nào của m thì hàm số đồng biến? Nghịch biến? b, Với giá trị nào của m thì hàm số đi qua A (1,2) C, Với giá trị nào của m thì hàm số đi qua B (1,2) D, Vẽ đô thị của 2 hàm số ứng với m vừa tìm đc ở câu a,b
a: Để hàm số đồng biến trên R thì m-3>0
=>m>3
Để hàm số nghịch biến trên R thì m-3<0
=>m<3
b: Thay x=1 và y=2 vào y=(m-3)x, ta được:
\(1\left(m-3\right)=2\)
=>m-3=2
=>m=5
c: Thay x=1 và y=2 vào y=(m-3)x, ta được:
m-3=2
=>m=5
d: Khi m=5 thì y=(5-3)x=2x
Bài 1: Cho hàm số\(y=x\sqrt{m-1}-\dfrac{3}{2}\).Tìm giá trị của m sao cho hàm số trên là hàm số bậc nhất
Bài 2: Với giá trị nào của k thì:
a)Hàm số \(y=\left(k^2-5k-6\right)x-13\) đồng biến?
b)Hàm số \(y=\left(2k^2+3k-2\right)x+3\) nghịch biến?
Bài 3: Cho hai hàm số bậc nhất y = 2x + k và y = (2m + 1)x + 2k - 3. Tìm điều kiện đối với m và k để hai đồ thị hàm số là:
a)Hai đường thẳng cắt nhau
b)Hai đường thẳng song song với nhau
c)Hai đường thẳng trùng nhau
Bài 4: Cho đường thẳng (d): y = (m - 3)x + 1 - m. Xác định m trong các trường hợp sau đây:
a) (d) cắt trục Ox tại điểm A có hoành độ x = 2
b) (d) cắt trục tung Ox tại điểm B có tung độ y = -3
c) (d) đi qua điểm C(-1 ; 4)