Một chiếc ăng – ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4 m. Ở mặt cắt qua trục ta được một parabol dạng y = a x 2 (h.24). Hãy xác định hệ số a.
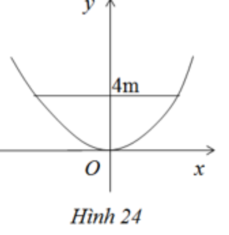
Một chiếc ăng - ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4m. Ở mặt cắt qua trục ta được một parabol dạng \(y=ax^2\) (h.24)
Hãy xác định hệ số a ?
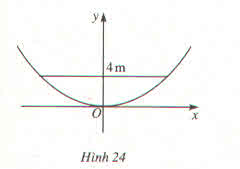
Pra bol đối xứng qua trục Tung => điểm cao nhất thuộc Parabol có tọa độ (2,h)
\(x=2\Rightarrow y=\dfrac{1}{2}\Rightarrow a.2^2=\dfrac{1}{2}\Rightarrow a=\dfrac{1}{8}\)
một chiếc ăng ten dạng chảo parabol có chiều cao h = 0,5 m và đường kính d= 4m mặt cắt qua trục là 1 parabol dạng y= 1/2 x2. Biết a= m/n trong đo m,n là các số dương nguyên tố cùng nhau. Tính m-n
mặt cắt của một chảo ăng ten là một phần của parabol cho biết đầu thu tín hiệu đặt tại tiêu điểm F cách đỉnh O của chảo một khoảng là 20 cm. Tính độ dài đường kính của chảo parabol trên biết khoảng cách từ một điểm bất kì trên miệng chảo đến đỉnh của chảo là 40 cm
Trong mặt phẳng tọa độ oxy cho parabol p y = x bình và đường thẳng d có dạng y = mx + m+1 a) với m =1 Tìm tọa độ giao điểm của đường thẳng d với hai trục tọa độ b) tính giá trị của m để đường thẳng d cắt parabol p tại 2 điểm phân biệt nằm về bên trái của đường thẳng x = 2
Trên mặt phẳng tọa độ Oxy cho parabol (P) y = x² và đườngthẳng (d) y = 4x +m-3.
1. Xác định m để đường thẳng d cắt trục OX tại điểm A, cắt trục Oy tại điểm B sao cho S aob=9.
2. Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x1; x2 thỏa mãn (4-x1)(x2-1)=2.
1: Tọa độ A là:
y=0 và 4x+m-3=0
=>x=(-m+3)/4 và y=0
=>OA=|m-3|/4
Tọa độ B là:
x=0 và y=m-3
=>OB=|m-3|
Theo đề, ta có: 1/2*(m-3)^2/4=9
=>(m-3)^2/4=18
=>(m-3)^2=72
=>\(m=\pm6\sqrt{2}+3\)
2:
PTHĐGĐ là:
x^2-4x-m+3=0
Δ=(-4)^2-4*(-m+3)=16+4m-12=4m+4
Để (P) cắt (d) tại hai điểm phân biệt thì 4m+4>0
=>m>-1
(4-x1)(x2-1)=2
=>4x2-4-x1x2+1=2
=>x2(x1+x2)-3-(-m+3)=2
=>x2*4-3+m-3=2
=>x2*4=2-m+6=8-m
=>x2=2-1/2m
=>x1=4-2+1/2m=1/2m+2
x1*x2=-m+3
=>-m+3=(1/2m+2)(2-1/2m)=4-1/4m^2
=>-m+3-4+1/4m^2=0
=>1/4m^2-m-1=0
=>m^2-4m-4=0
=>\(m=2\pm2\sqrt{2}\)
Câu 1: Cho parabol (P):y=x^2+bx+c (b,c là các tham số thực)
a. Tìm giá trị của b,c biết parabol (P) đi qua điểm M(-3;2) và có trục đối xứng là đường thẳng x=-1
b. Với giá trị của b,c tìm được ở câu a), tìm m để đường thẳng d:y=-x-m cắt parabol(P) tại 2 điểm phân biệt A,B sao cho tam giác OAB vuông tại O( với O là gốc toạ độ)
Cho parabol (P): y = x^2 và đường thẳng (d): y = x + m − 1. Tìm m để đường thẳng
(d) cắt parabol (P) tại hai điểm phân biệt ở bên trái trục tung.
Xét pt hoành độ gđ của parabol và d có:
\(x^2=x+m-1\)
\(\Leftrightarrow x^2-x+1-m=0\) (1)
Để (P) và (d) cắt nhau tại hai điểm pb bên trái trục tung
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S=1< 0\left(vl\right)\\P=1-m>0\end{matrix}\right.\)\(\Rightarrow\) Không tồn tại m để (d) cắt (P) tại hai điểm pb ở bên trái trục tung
Vậy...
Phương trình hoành độ giao điểm là:
\(x^2-x-m+1=0\)
a=1; b=-1; c=-m+1
\(\Delta=b^2-4ac\)
\(=\left(-1\right)^2-4\left(-m+1\right)\)
\(=1+4m-4\)
=4m-3
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow m>\dfrac{3}{4}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-1\right)}{1}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m+1}{1}=-m+1\end{matrix}\right.\)
Để (d) cắt (P) tại hai điểm phân biệt nằm ở bên trái trục tung thì
\(\left\{{}\begin{matrix}m>\dfrac{3}{4}\\x_1+x_2< 0\left(loại\right)\\x_1x_2>0\end{matrix}\right.\)
Vậy: \(m\in\varnothing\)
Khi cắt hình nón có chiều cao 16 cm và đường kính đáy 24 cm bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện là một hình Parabol có diện tích lớn nhất bằng

A. 120 2 c m 2
B. 120 6 c m 2
C. 120 3 c m 2
D. 150 3 c m 2
Mặt cắt cổng vào một khu triển lãm có hình dạng một parabol (P): y = -x^2. Mà trục đối xứng OH vuông góc với mặt đất. Biết bề rộng AB của cổng là 4m. Tính chiều cao HO của cổng.
Do tính đối xứng của parabol, \(\Rightarrow H\) là trung điểm AB \(\Rightarrow y_H=y_A=y_B\) đồng thời \(x_A=-x_B\)
Mặt khác \(AB=\left|x_A-x_B\right|=\left|2x_A\right|=4\Rightarrow x_A=2\)
\(\Rightarrow y_A=-x_A^2=-4\Rightarrow y_H=-4\)
\(\Rightarrow OH=\left|y_H\right|=4\) (m)